
eISSN:1856-9536



OPINIONES DE AGENTES SOCIALES: UNA PROPUESTA DESDE LA SOCIOFÍSICA PARA INVESTIGAR COMPORTAMIENTOS COLECTIVOS
Opinions of Social Agents: An Approach from Sociophysics to Investigate Collective Behaviors
Opiniões de agentes sociais: uma proposta desde a Sociofísica para investigar comportamentos coletivos
Karen P. Arias, Bernarda Pinilla, Mario G. Cosenza
OPINIONES DE AGENTES SOCIALES: UNA PROPUESTA DESDE LA SOCIOFÍSICA PARA INVESTIGAR COMPORTAMIENTOS COLECTIVOS
Anuario Electrónico de Estudios en Comunicación Social "Disertaciones", vol. 13, núm. 1, 2020
Universidad del Rosario
Karen P. Arias karenpag@gmail.com
Universidad Autónoma de la Ciudad de México, México
Bernarda Pinilla bpinilla59@gmail.com
Universidad de Los Andes, Venezuela
Mario G. Cosenza mario.cosenza@gmail.com
Universidad de Investigación de Tecnología Experimental Yachay, Ecuador
Recibido: 17 febrero 2019
Aceptado: 10 octubre 2019
Información adicional
Para citar este artículo: Arias, K. P., Pinilla, B., & Cosenza, M. G. (2020). Opiniones de agentes sociales: una propuesta desde la sociofísica para investigar comportamientos colectivos. Anuario Electrónico de Estudios en Comunicación Social “Disertaciones”, 13(1), 81-96. Doi: https://doi.org/10.12804/revistas.urosario.edu.co/disertaciones/a.7692
Resumen: En este artículo consideramos un problema específico de formación de opiniones: si los agentes sociales que califican un producto o servicio con una escala de opiniones discretas valoradas (por ejemplo, una escala de Likert) están conectados entre sí formando una red, real o virtual, ¿bajo qué condiciones pueden converger sus opiniones? Para abordar este problema, proponemos un modelo computacionalmente simple para la dinámica de opiniones discretas valoradas en una red de agentes que poseen un umbral para la interacción o comunicación entre ellos. El valor del umbral se interpreta como el nivel de tolerancia necesario para que ocurra una interacción entre agentes. Investigamos la influencia del umbral de tolerancia y de la topología de la red subyacente en el comportamiento colectivo del sistema. En redes complejas con conectividad local, incluyendo redes bidimensionales, redes de pequeño mundo, redes aleatorias y redes fractales surgen dos fases o estados colectivos diferentes, separados por un cierto valor crítico del umbral: (i) una fase caracterizada por la persistencia de diversidad de opiniones para valores del umbral menores que el valor crítico, y (ii) una fase en la que prevalece una opinión mayoritaria cuando el valor del umbral es mayor que el valor crítico. La fase diversa no surge en redes con conectividad global. Nuestros resultados permiten establecer condiciones para la emergencia de consenso o de polarización en sistemas sujetos a opiniones valoradas discretas.
Palabras clave: modelos de opinión, redes sociales, sistemas complejos, sociofísica.
Abstract: We consider the following opinion formation problem: if the social agents that rate a product or service on a discrete-valued scale (such as a Likert scale) are connected through a real or virtual network, under what conditions do their opinion converge? To address this problem, we propose a conceptual and computationally simple model for the dynamics of discrete opinions on a network of social agents that possess a threshold for interaction or communication between them. The model allows describing interactions between social agents in diverse situations where choices are discrete on determined valued scales. The interpretation of the threshold value is the degree of tolerance required for the occurrence of interaction between agents connected on either a real or virtual social network. We investigate the influence of both, the tolerance threshold and the network of the underlying network topology, on the collective behavior of the system. In complex networks with local connectivity, including bidimensional, small world, random, and fractal ones, we find two different phases or collective states: (i) a phase characterized by the persistence of diversity of opinions for threshold values less than the critical, and (ii) a phase with an opinion majority when the threshold value is greater than the critical value. The diversity phase does not arise in networks with local connectivity. Our results allow establishing conditions for the emergence of consensus or polarization in systems subjected to discrete opinion dynamics.
Keywords: Opinion models, social networks, complex systems, socio-physics.
Resumo: Neste artigo consideramos um problema específico de formação de opiniões: se os agentes sociais que avaliam um produto ou serviço com uma escala de opiniões discretas valoradas (por exemplo, uma escala de Likert) estão conectados entre si formando uma rede, real ou virtual, sob que condições podem convergir suas opiniões? Para abordar este problema, propomos um modelo computacionalmente simples para a dinâmica de opiniões discretas valoradas em uma rede de agentes que possuem um umbral para a interação ou comunicação entre eles. O valor do umbral interpreta-se como o nível de tolerância necessário para que ocorra interação entre agentes. Pesquisamos a influência do umbral de tolerância e da topologia da rede subjacente no comportamento coletivo do sistema. Em redes complexas com conectividade local, incluindo redes bidimensionais, redes de pequeno mundo, redes aleatórias e redes fractais, surgem dois fases ou estados coletivos diferentes, separadas por um determinado valor crítico do umbral: (i) uma fase caracterizada pela persistência de diversidade de opiniões para valores do umbral menores que o valor crítico, e (ii) uma fase onde prevalece uma opinião maioritária quando o valor do umbral é maior que o valor crítico. A fase diversa não surge em redes com conectividade global. Nossos resultados permitem estabelecer condições para a emergência de consenso ou de polarização em sistemas sujeitos a opiniões valoradas discretas
Palavras-chave: Modelos de opinião, redes sociais, sistemas complexos, Sociofísica.
En tiempos recientes, el estudio de los llamados sistemas complejos ha suscitado mucho interés en diversas disciplinas. Se ha descubierto que estos sistemas tan diversos como la World Wide Web; el Internet; las redes de telecomunicaciones; la propagación de epidemias y de virus informáticos; las redes y los grupos sociales; las corporaciones económicas; las redes de distribución de bienes y servicios; las colonias de insectos; los flujos metabólicos en las células; las conexiones neuronales en el cerebro; o los sistemas de osciladores acoplados poseen comportamientos colectivos comunes que se pueden describir mediante modelos físicos o matemáticos.
Los sistemas complejos son conjuntos de elementos interactivos cuyo comportamiento colectivo no está presente en los elementos aislados, sino que emerge de las interacciones entre ellos (Kaneko & Tsuda, 2000; Badii & Politi, 1997; Mikhailov & Calenbuhr, 2002). Las propiedades colectivas de estos sistemas no son susceptibles de ser derivadas de forma trivial a partir del análisis de sus elementos constituyentes. Los sistemas complejos se caracterizan por ser no lineales (el todo no es igual a la suma de las partes), interdependientes, adaptativos y emergentes (el comportamiento colectivo surge de las interacciones entre los elementos). Los sistemas complejos poseen comportamientos colectivos comunes como la sincronización; la formación de patrones; la autoorganización, las transiciones del orden al desorden y viceversa; y las redes de interacciones. El estudio de sistemas complejos ha revelado la existencia de estructuras de redes de conectividad y de propagación de información con características universales (Barabási, 2002; Newman, Barabási & Watts, 2006).
En los sistemas sociales existen estructuras colectivas que emergen de las interacciones entre los agentes del sistema y, por consiguiente, los conceptos y herramientas de sistemas complejos son aplicables a la investigación y el modelado de la dinámica social. La sociofísica o sociodinámica es el área de la física que estudia comportamientos emergentes en sistemas de agentes sociales, tales como competencia y cooperación; estructura y dinámica de redes sociales; consenso; polarización; globalización; multiculturalidad; propagación de información; propagación de epidemias; o influencias externas como medios masivos y formación de opinión, mediante técnicas de mecánica estadística, caos, sistemas complejos y simulaciones computacionales (Kadanoff, 2000).
Antecedentes
La sociofísica ha tenido particular interés en el estudio de modelos de formación de opinión (Ball, 2004). En este contexto, el trabajo del destacado científico social Robert Axelrod ha recibido mucha atención en las revistas de física. En 1977, Axelrod presentó un modelo de diseminación cultural (Axelrod, 1997) en el que los agentes de un sistema social establecen interacciones entre sí, basados en el principio de homofilia, es decir, cuando la probabilidad de interacción entre dos agentes es proporcional al grado de similitud cultural que comparten. En este modelo, las opciones culturales son estados discretos equivalentes, sin valoración. Otro modelo de dinámica de opiniones que ha suscitado gran interés es el de Deffuant, Neau, Amblard y Weisbuch (2000), en el cual las opiniones de los agentes pueden tomar un valor continuo en un intervalo entre dos valores extremos como, por ejemplo, un espectro político continuo desde la extrema izquierda hasta la extrema derecha. El modelo asume que la interacción entre agentes está sujeta a una condición de confianza limitada, es decir, la interacción entre dos agentes puede ocurrir si la diferencia de sus opiniones está dentro de un valor límite. Ambos modelos han dado lugar a una gran cantidad de aplicaciones y variaciones, tales como la investigación de los efectos de medios de comunicación masiva en la dinámica cultural; la diseminación de patrones culturales; la polarización y la globalización, entre otros, (Shibanai, Yasuno & Ishuguru, 2001; San Miguel, Eguíluz, Toral & Klemm, 2005; Castellano, Marsili & Vespignani, 2000; Klemm, Eguíluz, Toral & San Miguel, 2003a; Klemm, Eguíluz, Toral & San Miguel, 2003b; Castellano, Fortunato & Loreto, 2009; González-Avella, Cosenza, Klemm, Eguíluz & San Miguel, 2007; González-Avella, Cosenza, Eguíluz & San Miguel, 2010; González-Avella, Cosenza & San Miguel, 2012; González-Avella, Cosenza & San Miguel, 2014).
Contexto del problema y objetivo de investigación
Muchas empresas interesadas en consolidar su posición en el mercado solicitan a sus clientes evaluar la calidad de un producto o servicio, o su nivel de satisfacción, y para ello emplean métodos de valoración como la escala Likert, que incluye opciones que van desde “nada satisfecho” a “completamente satisfecho”. Generalmente, una compañía prefiere un sistema de calificación discreto y no continuo. Es inusual que se realice una prueba valorada con un rango del 1 al 5 y que permita valores como 2.1. 2.01. 2.001 o 2.0001; sería confuso diferenciar opiniones que tengan una diferencia tan pequeña entre ellas. La gran mayoría de estos sistemas de calificación consisten en opciones discretas valoradas.
Empresas como Amazon, Ebay, Mercado Libre, compañías de automóviles, de telefonía móvil, cadenas de restaurantes, instituciones bancarias, páginas web de comercio electrónico, entre otras, realizan este tipo de valoraciones. Con esa información se pueden establecer tendencias, patrones de consumo, productos preferidos o insumos menos populares. Con frecuencia, la publicidad emplea esta información con el fin de influenciar la escogencia de los clientes hacia una determinada opción en la escala de valoración. En muchos casos, los usuarios tienen acceso a la opinión de los otros. Por ejemplo, existen páginas web que muestran el puntaje promedio asignado a una película por el público. Las personas normalmente desean saber si una película es buena o no antes de verla. Una forma eficiente de saberlo es al revisar la valoración que esta posee y, para ello, consultan páginas web, como la base de datos de películas Internet Movie Database (imdb), encargadas de recopilar la opinión valorada de diferentes personas y de mostrar el puntaje promedio de una película. Los agentes en redes sociales también intercambian sus opiniones valoradas sobre diversos productos o servicios. En algunos casos se alcanza de forma espontánea un estado de consenso o se forma un grupo mayoritario que comparte una opinión, pero a veces persisten varios grupos con una diversidad de opiniones. Entender el comportamiento de estos sistemas tiene relevancia en las ciencias sociales.
En este contexto surge nuestra pregunta de investigación: si los agentes sociales que califican un tópico o un producto con una escala discreta de opiniones valoradas, tipo Likert, se comunican entre sí, ¿bajo qué condiciones pueden converger sus opiniones? Para abordar este problema, en este artículo proponemos un modelo sociofísico de opiniones discretas valoradas en el que los agentes poseen un umbral o condición para que puedan ocurrir interacciones entre ellos. El modelo es conceptual y computacionalmente simple, por cuanto su dinámica depende tan solo de un parámetro: el umbral para la interacción. En el contexto de sistemas sociales, este parámetro de umbral puede interpretarse como el grado o nivel de tolerancia que tienen los agentes del sistema para poder interactuar. El modelo que proponemos e investigamos en este artículo consiste en una combinación de las ideas básicas del modelo de Axelrod y del modelo de Deffuant et al. Nuestro objetivo, investigar el comportamiento colectivo de una red de agentes con opiniones discretas valoradas, como función del grado de tolerancia o umbral de interacción entre los agentes y de la topología o estructura de la red de conectividad subyacente.
Modelo de opiniones discretas valoradas
Proponemos un modelo de opinión basado en una combinación del modelo de Deffuant et al. y el modelo de Axelrod. Del modelo de Axelrod tomamos en cuenta que las opciones culturales o de opinión son discretas. Por otro lado, suponemos que los estados de opinión discretos tienen valor, es decir, se pueden representar como números enteros ordenados en un intervalo, de forma similar al modelo de Deffuant et al. Por simplicidad, consideramos un espacio de opinión unidimensional. Adicionalmente, suponemos que la interacción entre dos agentes ocurre dependiendo de una condición expresada mediante el valor de un umbral, al igual que en el modelo de Deffuant et al.
Como ilustración del modelo, consideremos una degustación de helados en una heladería. La heladería está interesada en conocer la opinión de los participantes con respecto a un nuevo helado de mantecado. A los clientes se les pide que califiquen el helado en una escala que va de “nada apetecible” a “muy apetecible”. A medida que se realiza la degustación, se nota que los participantes que encuentran el helado muy rico están en un mismo grupo y que los participantes que no lo encuentran tan apetecible se encuentran segregados en otro grupo. Supongamos que al día siguiente se realiza la misma degustación de helados con una diferente clientela. Ahora se observa que la calificación del helado no es tan polémica como el día anterior; los grupos están mezclados, los clientes a los que no les gusta el helado están interactuando con personas a las que sí les gusta. Esto indica que debe haber un grado de tolerancia diferente entre los agentes para ambos días. En nuestro modelo tratamos de medir cuantitativamente ese grado de tolerancia mediante un parámetro que denominamos umbral de interacción.
Formulación del modelo
El sistema consiste en N agentes colocados en una red. Denotamos por xi t al estado de la opinión valorada correspondiente al agente i. El estado de cada elemento puede tomar cualquiera de los Q valores enteros del conjunto {1, 2, 3,…,Q} donde Q es el valor máximo de las opiniones posibles. Introducimos el parámetro U como umbral de interacción. El umbral U puede tomar un valor del conjunto {1, 2, 3,…,Q}. El parámetro U se puede interpretar como el grado de tolerancia que poseen los agentes del sistema para interactuar entre sí. En este trabajo asumimos un umbral de tolerancia homogéneo, es decir, U es el mismo para todos los agentes.
En el tiempo inicial t = 0, asignamos al estado de cada agente un valor aleatorio en el conjunto {1, 2, 3,…,Q}.
Definimos la dinámica del sistema mediante el siguiente algoritmo iterativo:
1. Se selecciona aleatoriamente un agente i y uno de sus vecinos j en la iteración t.
2. Se calcula |xi t - xj t|.
Si |xi t - xj t| ≤ U, entonces xi t+1 ← xjt.
Si |xi t - xj t| > U, no sucede nada.
El tiempo máximo de iteración se establece cuando el sistema alcanza un estado estadísticamente estacionario.
Caracterización del comportamiento colectivo
La dinámica de opinión definida anteriormente corresponde a una dinámica absorbente, es decir, el número de estados presentes en el espacio de fase de los estados del sistema tiende a reducirse a medida que el sistema evoluciona. Desde el punto de vista físico, el sistema es disipativo. La dinámica de imitación implica la reducción en el número de estados del sistema en el tiempo; en este tipo de sistemas se alcanza un estado final estacionario en un tiempo finito.
Definimos un dominio como un conjunto de agentes conectados que comparten un mismo estado. Para caracterizar el comportamiento colectivo del sistema en su estado estacionario introducimos, como parámetro de orden estadístico, el tamaño normalizado (dividido por N) del dominio más grande en el sistema, denotado por S. La medida estadística S caracteriza la presencia de diversidad de grupos de opinión o el grado de consenso en el sistema. Cuando S → 0 no hay un dominio mayoritario, sino muchos grupos pequeños, lo cual indica la coexistencia de diversidad de opiniones en el sistema. Por otro lado, un valor S →1 caracteriza la presencia de un estado de opinión homogéneo en el sistema. La presencia de un grupo mayoritario, o mayoría simple, corresponde a S > 0,5. Exploramos el comportamiento colectivo mediante el cálculo de la cantidad S a medida que se varía el valor del umbral de tolerancia U.
Resultados
Dinámica de opiniones valoradas en redes con interacciones locales. Red bidimensional con vecindad de Von Neumann
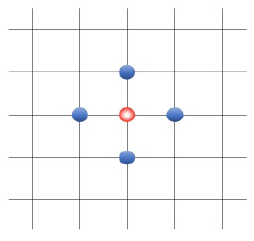
Estudiaremos el comportamiento colectivo del sistema con dinámica de opinión valorada definido sobre redes con interacciones locales, es decir, interacciones entre vecinos cercanos. La figura 1. muestra una red bidimensional con vecindad de Von Neumann (Toffoli & Margolus, 1987), en la que cada agente posee cuatro vecinos. Así pues, asumimos condiciones de frontera periódicas.
La figura 2. ilustra los patrones espaciotemporales resultantes estacionarios de la evolución de la dinámica de opiniones valoradas, definida sobre una red bidimensional con vecindad de Von Neumann para diferentes valores del umbral U. Vemos que el surgimiento de un estado homogéneo o de consenso, o de un estado de diversidad de opiniones depende del valor del parámetro de umbral U.

Para caracterizar el comportamiento colectivo estadístico del sistema consideremos una red bidimensional de tamaño N = 50 × 50 y la dinámica de opiniones valoradas con Q = 100 opciones. Aunque el umbral de interacción U es un número entero, es conveniente expresar esta cantidad en forma normalizada con respecto al número de opciones posibles Q. Definimos u como valor del umbral de interacción dividido por la cantidad de opciones posibles, tal que u ≡ U/Q.
La figura 3. muestra la cantidad estadística S, correspondiente al tamaño normalizado del dominio más grande presente en el sistema, en función del umbral de interacción normalizado u, para distintos parámetros. Para cada valor de u, la cantidad S ha sido calculada como el promedio resultante de 300 realizaciones de condiciones iniciales aleatorias. La figura 3(a). muestra S como función de u para varios valores del tamaño del sistema N, mientras que la figura 3(b). corresponde a S como función de u, cuando el número Q de opciones posibles varía.
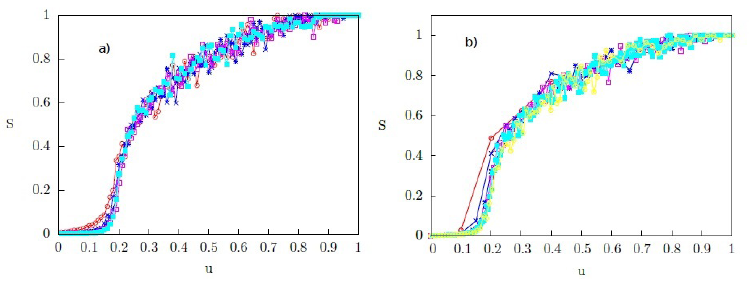
En ambos paneles de la figura 3. se observa que el sistema siempre alcanza un estado de diversidad de opiniones para valores de u menores que un valor uc = 0,23, caracterizado por S → 0. Adicionalmente, para valores de u mayores que uc, la cantidad S se incrementa hasta alcanzar el valor S = 1. En el contexto de mecánica estadística el valor uc se puede interpretar como el valor crítico de una transición de fase de segundo orden, donde la función S que representa el parámetro de orden es continua, pero su primera derivada no lo es. Encontramos dos fases o estados colectivos con propiedades diferentes, separadas por un cierto valor crítico del umbral: (i) una fase caracterizada por la persistencia de una diversidad de opiniones para valores del umbral menores que el valor crítico; y (ii) una fase con una opinión mayoritaria cuando el valor del umbral es mayor que el valor crítico.
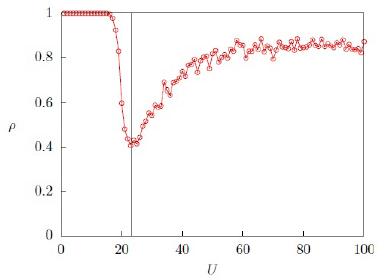
El valor crítico de un parámetro asociado a una transición de fase corresponde al valor de ese parámetro para el cual las cantidades macroscópicas del sistema exhiben la mayor fluctuación en sus valores (Kadanoff, 2000). Para determinar el valor crítico uc en la figura 4. calculamos la probabilidad de alcanzar un estado estacionario del sistema, denotada por ρ, en un número de 750 realizaciones de condiciones iniciales para cada valor de U.
En el presente caso, la mayor fluctuación estadística implica el menor valor de la probabilidad ρ, el cual ocurre para Uc= 23 en la figura 4. Luego, uc = 23/100 = 0,23.
La figura 3(a). revela que, al aumentar el tamaño del sistema, la transición en el valor crítico uc resulta mejor definida. Sin embargo, el valor uc = 0,23 no varía sustancialmente al cambiar el tamaño del sistema. De forma similar, en la figura 3(b). se observa que el número de opciones Q disponibles para los agentes no tiene gran influencia en el valor de umbral crítico necesario para el surgimiento de un consenso en el sistema. Estos resultados implican que la transición de fase descrita por la cantidad S en función de u es robusta. Los resultados de la figura 3. se pueden interpretar de la siguiente manera: para que pueda surgir un grupo mayoritario en el sistema, el umbral para interacción entre los agentes debe tener un valor mayor al 23 % del tamaño de las opciones disponibles. En otras palabras, si el grado de tolerancia entre los agentes es menor que un 23 %, estos no pueden alcanzar una opinión común o un estado de consenso, y una diversidad de opiniones prevalece en el sistema. Nótese que la mayoría simple S = 0,5 se alcanza para un umbral de interacción de u = 0,26, cercano al valor crítico uc.
Redes complejas con conectividad local
Para investigar la influencia de la topología de la red en el comportamiento colectivo de un sistema con opiniones discretas valoradas, consideramos nuestro modelo definido sobre diversas redes complejas con conectividad local que son relevantes en sistemas sociales. Nos enfocaremos en redes cuyo número (o número promedio) de vecinos por nodo es igual a cuatro, al igual que la red bidimensional anteriormente estudiada, las cuales se ilustran en la figura 5. En este trabajo consideraremos solamente redes conexas.
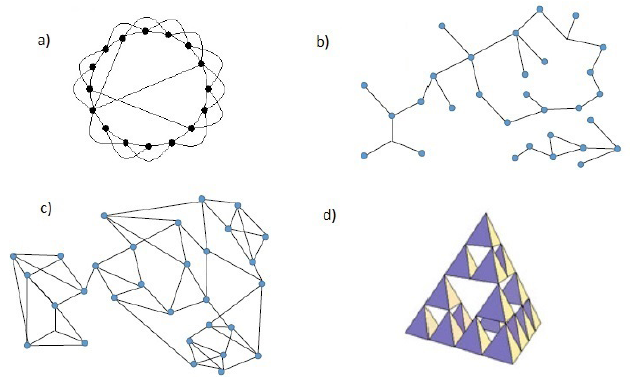
La figura 5(a). muestra una red de pequeño mundo construida mediante el algoritmo de Watts-Strogatz con grado k = 4 y probabilidad de recableado p (Watts & Strogatz, 1998). La probabilidad de recableado p es la probabilidad de que un enlace entre dos nodos seleccionados al azar se corte y se ubique en otro lugar. En nuestro caso, la red resultante conserva el número de vecinos por nodo k. El valor p = 0 describe una red tipo anillo donde cada nodo está conectado con sus dos vecinos inmediatos a cada lado. Cuando p = 1, tenemos una red completamente aleatoria con k = 4 vecinos por nodo. El efecto pequeño mundo, cuando la distancia media entre dos nodos es mucho menor que el tamaño de la red, ocurre para valores intermedios de p (Newman, 1999). La figura 5(b) corresponde a una red aleatoria tipo Erdös-Rényi (1960), donde cada nodo posee, en promedio, cuatro vecinos, es decir, ⟨k⟩=4. Una red aleatoria con cuatro vecinos por nodo se representa en la figura 5(c). Por su parte, la figura 5(d). ilustra una red fractal del tipo Sierpinski contenida en un espacio tridimensional y cuya dimensión fractal es igual a 2 (Cosenza & Kapral, 1992).
La figura 6. muestra las gráficas de la cantidad estadística S en función del valor de umbral normalizado u para distintas redes complejas con cuatro vecinos por nodo consideradas en el presente trabajo.
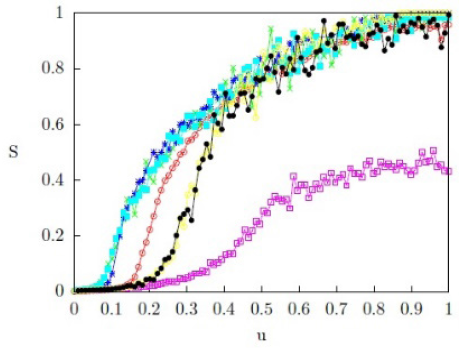
En la figura 6. se puede observar que, para valores del umbral u suficientemente grandes, todas las redes, excepto la red tipo anillo con k = 4 y p = 1, alcanzan un estado de homogeneidad. En el caso de un anillo con cuatro vecinos, la interfase entre diferentes dominios consiste siempre en dos nodos, por lo que la interfase no está bien definida. Esto restringe la posibilidad de crecimiento de dominios en la red, por lo que no es posible alcanzar un estado colectivo homogéneo con un solo dominio. Notamos que la red aleatoria tipo Erdös-Rényi, la red aleatoria con ⟨k⟩=4 y la red Watts-Strogatz con p = 0 exhiben un comportamiento colectivo muy similar. Estas redes presentan una topología común característica de redes aleatorias, por lo que cabe esperar que sus comportamientos colectivos sean similares.
Por otro lado, la figura 6. muestra que el comportamiento colectivo de la red de pequeño mundo (p = 0,01) es similar al comportamiento de la red fractal tipo Sierpinski. Esto sugiere que la dinámica de opiniones valoradas en la red fractal tipo Sierpinski forma dominios autosimilares que permiten reducir la distancia media efectiva entre dominios del sistema, lo que produce un efecto de pequeño mundo. En este sentido, la topología efectiva de estas dos redes puede considerarse similar y, por tanto, sus comportamientos colectivos también son similares.
La figura 6. representa uno de los resultados centrales del presente trabajo: la topología de la red de conectividad subyacente, y no el número de vecinos o conexiones locales, influyen en el comportamiento colectivo de un sistema sujeto a una dinámica de opiniones valoradas. Adicionalmente, vemos que el grado de tolerancia o valor del umbral crítico uc depende de la topología de la red.
Dinámica de opinión valorada con interacciones globales
Una red global está construida de forma que cualquier nodo esté conectado con todos los otros nodos de la red. Inicialmente, consideramos un anillo de N nodos donde cada nodo posee k = N - 1 vecinos. Desde el punto de vista topológico la red global representa una estructura más simple. Redes de este tipo aparecen en muchos sistemas naturales y artificiales. En particular, muchas redes sociales son redes efectivamente globales; en ellas un agente puede intercambiar información con cualquier otro en la red. La figura 7(a). ilustra una red global.
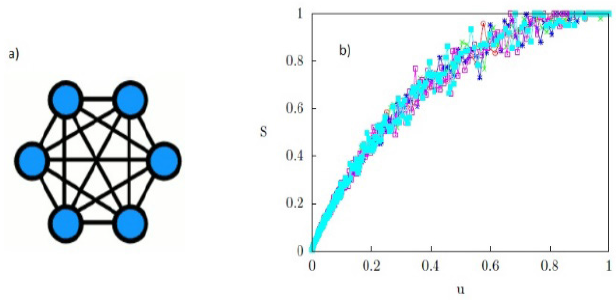
Consideremos una red de tamaño N = 1000 y una dinámica de opiniones valoradas con Q = 100 opciones disponibles. La figura 7(b). muestra la cantidad estadística S, correspondiente al tamaño normalizado del dominio más grande presente en el sistema, en función del umbral de interacción u, para distintos valores de Q. Al igual que los casos de redes con conectividad local, para cada valor de u la cantidad S se calcula como el promedio resultante de 50 realizaciones de condiciones iniciales aleatorias. En la figura 7(b). se observa que cuando u → 0, el sistema posee un estado donde aparece un dominio mayoritario. A medida que aumenta el umbral u, el grupo mayoritario en el sistema aumenta de tamaño hasta que, cuando u → 1, un estado homogéneo emerge en el sistema. La mayoría simple S = 0,5 se alcanza para u = 0,2. La figura 7(b). revela que la cantidad de opciones posibles Q tiene poco efecto en el comportamiento colectivo del sistema en una red global. También hemos verificado que el tamaño del sistema no influye en el comportamiento del sistema en una red global.
Nótese que para una red global no existe la fase desordenada, es decir, uc = 0. En esta red, el número promedio de agentes distribuidos inicialmente en cada estado es N/Q. Dado un umbral U, el número de agentes con los que puede interactuar un agente cualquiera en el sistema es proporcional a U × N/Q. Luego, la probabilidad que tiene un agente cualquiera de interactuar con otro agente en el sistema es proporcional a 1/N × U × N/Q = u. Es decir, el umbral normalizado u mide la probabilidad de interacción inicial entre agentes del sistema. La probabilidad de interacción y, por lo tanto, la posibilidad de crecimiento de algún dominio, existe para todo valor u > 0. En contraste, para una red local con k vecinos por nodo, la probabilidad de interacción inicial entre agentes del sistema es proporcional a k/N × u. Esta probabilidad puede ser muy pequeña cuando u es pequeño y, por lo tanto, el sistema puede alcanzar un estado desordenado para valores de u suficientemente pequeños. Luego, para estas redes puede ocurrir en general una transición de fase en el parámetro de orden S como función de u.
Al comparar los resultados de la figura 6. con aquellos de la figura 7(b)., vemos que el comportamiento colectivo de una red compleja con conectividad local es sustancialmente diferente al comportamiento colectivo de una red global: en las primeras puede ocurrir una transición de fase que permite un estado de diversidad; mientras que en la última no existe transición de fase y siempre hay crecimiento de un grupo de opinión mayoritario.
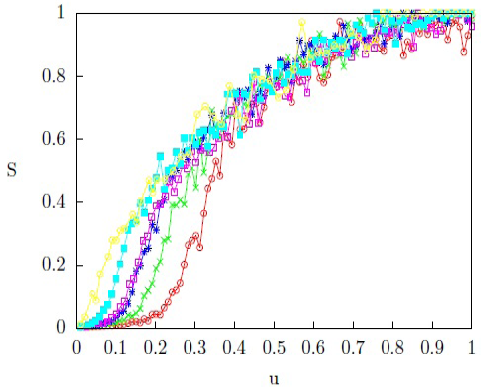
Con el fin de entender este cambio de comportamiento del sistema al pasar de una red local a una red global, investigamos nuestro modelo de opiniones valoradas en una red tipo Watts-Strogatz variando el número de vecinos por nodo k. De esta manera, al aumentar k nos aproximamos al límite de una red global. Entonces, consideramos una red de pequeño mundo con p = 0;01, con tamaño N = 1000 y una dinámica de opiniones valoradas con Q = 100. La figura 8. muestra las gráficas de S versus u para esta red, con diferentes números de vecinos k. Se observa una transición de fase para un umbral de interacción crítico uc cuyo valor disminuye a medida que aumenta k, como puede esperarse a medida que nos acercamos a la topología de una red global. En efecto, cuando k aumenta, la cantidad de nodos con los que un agente puede interactuar se incrementa, de manera que el sistema se comporta como una red global en el límite k → N – 1.
Conclusiones
Hemos propuesto un modelo sociofísico de opiniones valoradas discretas con un umbral o condición para las interacciones. Nuestro modelo es conceptual y computacionalmente simple, por cuanto su dinámica depende tan solo de un parámetro u que mide el umbral para la interacción. En el contexto de sistemas sociales, el parámetro de umbral puede interpretarse como el grado de tolerancia para que ocurra interacción entre los agentes del sistema. El modelo presentado puede considerarse como una combinación del modelo de diseminación cultural de Axelrod y del modelo de opiniones continuas de Deffuant et al. Nuestro modelo permite describir en forma general la interacción de agentes en diversas situaciones sociales donde las opiniones son discretas en ciertas escalas de valoración. Por ejemplo, la escala de Likert que se usa en muchas encuestas; la escala de satisfacción de consumidores de productos comerciales de empresas como Amazon, Ebay, imdb, Mercado Libre; las encuestas políticas o socioeconómicas de empresas consultoras de opinión, etc. Hemos investigado el comportamiento colectivo emergente de esta dinámica sobre redes con diferentes topologías: red bidimensional con vecindad de Von Neumann; red de pequeño mundo; red aleatoria de Erdös-Rényi; red aleatoria; red fractal; y red global.
En redes con interacciones locales hemos encontrado una transición de fase, desde un estado colectivo de diversidad o desorden para valores del umbral menores que un cierto valor crítico uc, hacia un estado colectivo con una opinión mayoritaria para valores del umbral mayores que uc. Para valores del umbral suficientemente grandes, es posible alcanzar un estado colectivo homogéneo o de consenso. En el caso de una red unidimensional regular, la frontera que separa diferentes dominios siempre consiste en dos nodos, de forma que la posibilidad de crecimiento de los dominios en la red se restringe. Como consecuencia, el sistema no puede alcanzar un estado colectivo de consenso.
Las redes aleatorias y la red de pequeño mundo con probabilidad de recableado igual a 1, también exhiben una transición de fase, pero para un valor pequeño del umbral. Cabe esperar que los comportamientos colectivos de estas redes sean similares debido a que sus topologías comparten características comunes a las redes aleatorias.
El comportamiento colectivo de la red de pequeño mundo es parecido al comportamiento de la red fractal. Esta similitud sugiere que la pirámide de Sierpinski forma dominios autosimilares que permiten reducir la distancia media efectiva entre dominios del sistema. En este sentido, las topologías de estas dos redes pueden considerarse similares, por lo tanto, sus comportamientos colectivos también son parecidos.
Hemos encontrado que en una red con interacciones globales no ocurre la transición de fase descrita, sino que existe formación de un dominio mayoritario para cualquier valor del umbral u. Para explicar este comportamiento hemos argumentado que en esta red el umbral representa la probabilidad de interacción inicial entre agentes, por lo tanto, la posibilidad de crecimiento de algún dominio existe para todo valor u > 0.
Al investigar las redes de pequeño mundo a medida que se incrementa el número de vecinos o la probabilidad de reclableado hemos mostrado que la transición de fase entre diversidad y consenso de opiniones desaparece cuando la red se aproxima a una red global. Luego, el comportamiento colectivo observado en una red global está relacionado con la presencia de interacciones de largo alcance.
Nuestros resultados permiten concluir que un estado colectivo de consenso en una red de agentes sociales que califican un producto o un servicio con una escala discreta de opiniones valoradas surge cuando el grado de tolerancia para la interacción entre agentes es suficientemente grande (mayor que un valor crítico típicamente de un 23 %), independientemente de la estructura de la red. Por otro lado, un estado colectivo de diversidad de opiniones ocurre cuando el grado de tolerancia para la interacción entre agentes es pequeño (menor que el valor crítico) y las interacciones son locales, es decir, entre primeros vecinos en la red.
El conocimiento de las condiciones que llevan a estos estados colectivos puede ser útil para empresas comerciales, organizaciones políticas o encuestadoras que realizan valoraciones de opiniones en una escala discreta. En particular, conocer el valor crítico de tolerancia para el consenso o el surgimiento de un grupo mayoritario de opinión en un sistema social puede ser relevante para el diseño de publicidad o propaganda que permita influenciar la escogencia de una determinada opción en la escala de valoración.
Agradecimientos
Agradecemos a la Corporación Ecuatoriana para el Desarrollo de la Investigación y Academia (cedia) por el financiamiento otorgado a la presente investigación mediante el proyecto cepRa – Xiii -2019-10: Interacciones Globales en Sistemas Complejos.
Referencias
1. Axelrod, R. (1997). The dissemination of culture: a model with local convergence and global polarization. Journal of Conflict Resolution, 41(2), 203-226. Doi: 10.1177/0022002797041002001
2. Badii, R. & Politi, A. (1997). Complexity: Hierarchical Structures and Scaling in Physics. Cambridge: Cambridge University Press.
3. Ball, P. (2004). The physical modelling of human social systems. Complexus Review, 1(4), 190-206. Doi:10.1159/000082449
4. Barabási, A. (2002). Linked: The New Science of Networks. Nueva York: Perseus Publishing Co.
5. Castellano, C., Fortunato, S., & Loreto, V. (2009). Statistical physics of social dynamics. Reviews of Modern Physics, 81(2), 591-646. Doi: 10.1103/RevModPhys.81.591
6. Castellano, C., Marsili, M., & Vespignani, A. (2000). Nonequilibrium Phase Transition in a Model for Social Influence. Physical Review Letters, 85(16), 3536-3539. Doi: 10.1103/PhysRevLett.85.3536
7. Cosenza, M. G., & Kapral, R. (1992). Coupled Maps on Fractal Lattices. Physical Review A, 46(4), 1850-1858. Doi:10.1103/PhysRevA.46.1850
8. Deffuant, G., Neau, D., Amblard, F., & Weisbuch, G. (2000). Mixing beliefs among interacting agents. Advances in Complex Systems, 3(01n04), 87-98. Doi: 10.1142/S0219525900000078
9. Erdös, P. & Rényi, A. (1960). On the evolution of random graphs. Publication of the Mathematical Institute of the Hungarian Academy of Sciences, 5, 17-61. Doi: 10.1.1.153.5943
10. González-Avella, J. C., Cosenza, M. G., Eguíluz, V. M., & San Miguel, M. (2010). Spontaneous ordering against an external field in non-equilibrium systems. New Journal of Physics, 12(1), 013010. Doi: 10.1088/1367-2630/12/1/013010
11. González-Avella, J. C., Cosenza, M. G., Klemm, K., Eguíluz, V. M., & San Miguel, M. (2007). Information feedback and mass media effects in cultural dynamics. Journal of Artificial Societies and Social Simulation, 10(3), 1-17. Recuperado de http://jasss.soc.surrey.ac.uk/10/3/9.html
12. González-Avella, J. C., Cosenza, M.G., & San Miguel, M. (2012). A Model for Cross-Cultural Reciprocal Interactions through Mass Media. PLOS ONE, 7(12), e51035. Doi: 10.1371/journal.pone.0051035
13. González-Avella, J. C., Cosenza, M.G., & San Miguel, M. (2014). Localized coherence in two interacting populations of social agents. Physica A: Statistical Mechanics and its Applications, 399, 24-30. Doi: 10.1016/j. physa.2013.12.035
14. Kadanoff, L. P. (2000). Statistical physics: Statistics, Dynamics and Renormalization. Singapur: World Scientific Publishing.
15. Kaneko, K. & Tsuda, I. (2000). Complex systems: Chaos and beyond. A Constructive Approach with Applications in Life Sciences. Berlín: Springer. Doi: 10.1007/978-3-642-56861-9
16. Klemm, K., Eguíluz, V. M., Toral, R., & San Miguel, M. (2003a). Global culture: A noise-induced transition in finite systems. Physical Review E, 67 (4), 045101. Doi: 10.1103/PhysRevE.67.045101
17. Klemm, K., Eguíluz, V. M., Toral, R., & San Miguel, M. (2003b). Nonequilibrium transitions in complex networks: A model of social interaction. Physical Review E, 67 (2), 026120. Doi: 10.1103/PhysRevE.67.026120
18. Likert, R. (1932). A technique for the measurement of attitudes. Archives of Psychology, 22 (140), 5-55. Recuperado de https://psycnet.apa.org/record/1933-01885-001
19. Mikhailov, M. & Calenbuhr, V. (2002). From cells to societies: Models of complex behaviour. Berlín: Springer.
20. Newman, M. E. J. (1999). Small worlds: the structure of social networks. Working Papers 99-12-0803. Santa Fe: Santa Fe Institute.
21. Newman, M., Barabási, A., & Watts, D. J. (2006). The structure and dynamics of networks. Princeton: Princeton University Press.
22. San Miguel, M., Eguíluz, V.M., Toral, R., & Klemm, K. (2005). Binary and multivariate stochastic models of consensus formation. Computing in Science & Engineering, 7(6), 67-73. Doi: 10.1109/mcse.2005.114
23. Shibanai, Y., Yasuno, S., & Ishiguro, I. (2001). Effects of Global Information Feedback on Diversity: Extensions to Axelrod’s Adaptive Culture Model. Journal of Conflict Resolution, 45(1), 80-96. Doi: 10.1177/0022002701045001004
24. Toffoli, T. & Margolus, N. (1987). Cellular Automata Machines: A New Environment for Modeling. Cambridge: MIT Press.
25. Watts, D. J. & Strogatz, S. H. (1998). Collective dynamics of ‘small-world’ networks. Nature, 393 (6684), 440-442. Doi:10.1038/30918



