
ISSN:0123-5362 | eISSN:2145-454X



Estimación del efecto de la segregación ocupacional por sexo en el ingreso laboral para Argentina (2016-2020)
Estimation of the Effect of Occupational Segregation by Sex on Labor Income for Argentina (2016-2020)
Estimativa do efeito da segregação ocupacional por sexo na renda salarial na Argentina (2016-2020)
Federico Favata, Sofía Zamparo
Estimación del efecto de la segregación ocupacional por sexo en el ingreso laboral para Argentina (2016-2020)
Revista de Economía del Rosario, vol. 25, núm. 1, 2022
Universidad del Rosario
Federico Favata a ffavata@unsam.edu.ar
Centro de Investigaciones Macroeconómicas para el Desarrollo, Argentina
Sofía Zamparo zamparo.sofi@gmail.com
Universidad Torcuato Di Tella, Argentina
Recibido: 16 octubre 2020
Aceptado: 31 marzo 2022
Información adicional
Para citar este artículo: Favata, F., & Zamparo, S. (2022). Estimación del efecto de la segregación ocupacional por sexo en el ingreso laboral para Argentina (2016-2020). Revista de Economía del Rosario, 25(1), 1-25.https://doi.org/10.12804/revistas.urosario.edu.co/economia/a.12129
Resumen:
El objetivo de este trabajo es estimar el efecto de la segregación ocupacional por sexo en el ingreso laboral horario promedio en Argentina, para el periodo comprendido entre el 2016 y 2020. Para ello, utilizando la Encuesta Permanente de Hogares (eph) se estimó cómo impacta la segregación por sexo, a través de la regresión cuantílica bajo variables instrumentales. Los resultados indican que un aumento de 10 puntos porcentuales en la proporción de mujeres en una ocupación determinada, el ingreso promedio horario de los trabajadores de tal ocupación disminuye en promedio 0.50 %. Adicionalmente, esta magnitud varía acorde al cuantil de la distribución salarial condicional donde se posicione.
Código JeL: J01, J31
Palabras clave: segregación, salario, regresiones cuantílicas bajo variables instrumentales.
Abstract:
We use conditional instrumental variables quantile regression to estimate the effect of occupational segregation by sex in the average working wage for Argentina between 2016-2020, using the Encuesta Permanente de Hogares (eph) database. The results show that a 10 percent points rise in women’s share in a specific occupation decreases the overall average working wage for that occupation by 0.50 %. Additionally, we see that the magnitude of the impact varies depending on the percentile of the conditional wage distribution, where we see higher effects in the low quantile percentile.
JeL classification:J01, J31.
Keywords: Segregation, wage, instrumental variables quantile regressions.
Resumo:
O objetivo deste trabalho é estimar o efeito da segregação ocupacional por sexo na renda média salarial por hora na Argentina, para o período entre 2016 e 2020. Usando a Pesquisa de Domicílios Permanentes (pdp), estima-se como a segregação por sexo é afetada, por meio de regressão quantílica sob variáveis instrumentais. Os resultados indicam que com um aumento na proporção de mulheres em 10 pontos percentuais para uma determinada ocupação, a renda por hora dos trabalhadores nessa ocupação diminui em média 0.50 %. Além disso, essa magnitude varia de acordo com o ranking da distribuição salarial condicional onde está posicionada.
Clasificação JeL: J01, J31.
Palavras-chave: segregação, salário, regressões quantílicas sob variáveis instrumentais.
Introducción
La heterogeneidad en el mercado laboral podría ser originada por diversos factores: nivel educativo, tipo de ocupación, jornada, contrato, ubicación, edad y sexo, entre otros. Por eso hay múltiples formas para visibilizar y cuantificar los aspectos disruptivos del mercado, en los que se destaca la brecha salarial, la distribución de individuos con alguna característica de interés en estructuras jerárquicas y la segregación ocupacional.
Reskin (1993) define a la segregación por sexo en el mercado laboral como algo más que una mera separación física, más bien, hace referencia a un proceso fundamental en la desigualdad social en el que diferentes grupos de personas se someten a distintos sistemas de recompensa.
El término segregación, a su vez, se puede dividir en dos tipos: segregación horizontal y vertical. La segregación horizontal se refiere a la concentración de cierto grupo en determinados sectores de la actividad económica, y su dificultad para acceder a otras ocupaciones. Esto se verifica en la predominancia de las mujeres hacia los sectores tradicionales feminizados y las trabas para acceder a cargos con alta tasa de masculinización. Por otro lado, la segregación vertical menciona la imposibilidad de determinados grupos para desarrollarse profesionalmente. En particular, se manifiesta mediante el llamado “techo de cristal”, que impide el acceso de las mujeres a los puestos de mayor responsabilidad y toma de decisiones.
Dicho esto, como se mencionó, el objetivo del presente trabajo será estimar el efecto de la segregación ocupacional por sexo en el ingreso laboral horario promedio en Argentina, para el periodo comprendido entre el 2016 y 2020. Utilizando la información disponible en la Encuesta Permanente de Hogares (eph), se clasificó a los individuos de acuerdo con la ocupación principal que reportaran, y luego, se calculó la proporción de mujeres por sector. Una vez generada esta variable, se reportó el impacto sobre el ingreso horario de una ocupación a medida que aumenta la proporción de mujeres, mediante cuatro modelos: regresión por mínimos cuadrados clásicos, regresión lineal en dos etapas, regresión cuantílica y regresión cuantílica bajo variables instrumentales.
La estructura del documento es la siguiente: la segunda sección contiene un marco teórico y empírico sobre la segregación. La tercera sección posee información sobre la metodología utilizada, especificación econométrica y las fuentes de datos. En la cuarta sección se presentan los resultados, y en la quinta, las conclusiones.
1. Marco teórico y empírico
1.1. Causas de la segregación ocupacional
La evidencia empírica revela la existencia de un mercado imperfecto, donde hombres y mujeres no se distribuyen al azar en las distintas ocupaciones. Son estas diferencias entre proporciones ocupacionales las que constituyen el fenómeno conocido como segregación ocupacional por sexo. Tal dispersión sectorial es abordada por la literatura clásica desde diferentes ángulos:
(i) fundamentos desde el lado de la demanda de trabajo y (ii) las correspondientes al lado de la oferta, es decir, de las y los trabajadores.
Para el primero, Reskin (1993) sostiene que los empleadores son quienes asignan los trabajadores a las diferentes tareas, y que son sus acciones las que contribuyen sustancialmente a la concentración de hombres y mujeres en diferentes ocupaciones. El argumento está relacionado con el concepto de discriminación estadística, definido como una situación en la que las decisiones con respecto a individuos se basan en probabilidades derivadas de un grupo. Si existen grupos de empleadores que perciban a las mujeres como trabajadoras menos estables, serán excluidas de esos tipos de trabajo (Blau & Jusenius, 1976; Coverman, 1983).
Para el segundo, alusivo a la oferta de trabajo, existen diferentes teorías que convergen en que son los empleados quienes se autoseleccionan para ocupaciones de diversa naturaleza. Dos de ellas son el enfoque neoclásico y el de gender socialization. Según la corriente neoclásica, en la mayoría de los matrimonios heterosexuales los hombres pertenecen activamente al mercado laboral y las mujeres se ocupan del hogar; por esta razón difieren en la expectativa de continuidad del empleo. Esta visión está alineada con la teoría de diferenciales compensatorios, cuya hipótesis es que las mujeres suelen buscar trabajos con la libertad y flexibilidad necesarias para poder ocuparse de sus hogares y de los niños, aún si esto implica menor remuneración. Por otro lado, el enfoque de gender socialization argumenta que la brecha entre hombres y mujeres se origina de acuerdo a estándares y normas socioculturales: cada sector desarrolla las preferencias y habilidades que son esperables para su sexo. La segregación es simplemente el resultado de tales preferencias (Okamoto & England, 1999).
Hanson y Pratt (1991) se alejan de estas posturas y suman otra perspectiva que explica la segregación por sexo: motores de búsqueda laborales. Los canales de información para enterarse de ofertas de trabajo difieren entre hombres y mujeres, para mujeres en ocupaciones dominadas por mujeres y para mujeres en ocupaciones con mayor presencia masculina. Gran parte de la información acerca de trabajos potenciales se obtiene en la vida cotidiana, por lo tanto, no solo dependerá de habilidades o preferencias, sino también de las tareas que cada uno tenga asignadas, y como generan contactos los jugadores en su día a día mediante estas.
Independientemente de las diferencias en las teorías, todas tienen un punto en común: la segregación en el mercado laboral se relaciona en la forma en que se dividen los roles y las tareas entre hombres y mujeres. De acuerdo con un informe realizado por la Organización Internacional del Trabajo (oit) focalizado en salarios y desigualdad de ingresos, la brecha salarial entre hombres y mujeres puede ser dividida entre una parte explicada —representada por características observables— y una parte no explicada —que sugiere la existencia de discriminación en el mercado laboral—. Estas disparidades no pueden explicarse únicamente en términos de diferencias de edad o educación, sino que también están vinculadas con la infravaloración del trabajo que realizan las mujeres y con las calificaciones que se requieren en los sectores u ocupaciones dominados por mujeres, con la práctica de la discriminación (oit, 2015).
Blau y Kahn (2017) sugieren que los atributos psicológicos o habilidades no cognitivas también podrían aportar a esta distribución desigual salarial, y parte de su análisis es demostrar cuantitativamente el impacto de estas. No obstante, en su extenso análisis sobre tendencias y explicaciones de la brecha salarial para Estados Unidos entre 1980 y el 2010, también hacen alusión a que —aunque el agregado no tenga tanto impacto— las variables “tradicionales” que explican diferencias en factores de capital humano —como la intermitencia de las mujeres en el mercado laboral por maternidad u otros motivos y preferencias por trabajos de menor carga laboral— siguen teniendo un peso en la brecha —alineado con la teoría de diferenciales compensatorios—. A la vez, añaden que la segregación a través de ocupaciones e industrias sigue siendo un aspecto importante por tratar, dado que la distribución desigual de roles y divisiones en el mercado laboral sugieren la existencia de discriminación en el mismo.
1.2. Evidencia empírica general
En las últimas décadas se han realizado múltiples trabajos en busca de cuantificar la segregación ocupacional y probar la existencia de su relación con la brecha salarial. Clarhall (2011) realizó un análisis del impacto de la segregación ocupacional por sexo en Noruega, y los resultados de sus estimaciones mostraron que no solo hay diferencias en el mercado laboral por sexo, sino también por las ocupaciones, aquellas con mayor predominancia femenina tienen una remuneración promedio menor. Su base de datos contenía individuos empleados de sectores públicos y privados, para el periodo de 1997-2006. Usó como variable dependiente el logaritmo del ingreso horario y propuso la existencia de una relación lineal entre esta y diferentes covariables, una de ellas, la proporción de mujeres por ocupación como proxy de métrica de segregación.
La especificación econométrica original es un modelo de regresión lineal, en el que la autora reconoce un potencial problema de endogeneidad por dos factores. Primero, cabe la posibilidad de no haber incluido todas las variables relevantes (variables omitidas). El segundo es causalidad simultánea, la proporción de mujeres que podría impactar al ingreso, así como el ingreso en la segregación. Si el nivel de ingreso es más relevante para los hombres, naturalmente se dará una segregación por sexo acorde al tipo de ingreso que ofrezca cada ocupación, en el que los hombres se concentrarán donde se ofrezca más ingreso. Ante este escenario, se instrumenta utilizando dos variables, la proporción promedio de mujeres empleadas graduadas en cada ocupación, para los cinco y diez años previos. Los resultados arrojan evidencia significativa de un efecto negativo de la proporción de mujeres sobre el ingreso: un aumento del 10 % de la proporción de mujeres en una ocupación reduce el ingreso horario de esa ocupación en un 2.7 %. Los resultados se sostienen ante la estimación en dos etapas, y contemplando por efectos fijos. Del Río y Alonso-Villar (2010) llevaron a cabo un estudio sobre la segregación ocupacional por sexo en España, en el cual midieron no solo la segregación total, sino también la segregación particionada por sexo y edad, sexo y nivel educativo, sexo y tipo de contrato, sexo y tipo de trabajo y sexo y nivel salarial. Dentro del grupo de mujeres, se encuentra evidencia de mayor segregación entre jóvenes y ancianas, mientras que, para los hombres, la segregación es mayor para jóvenes. Individuos con un nivel de educación intermedio sufren una segregación menor que aquellos con más educación, tanto para hombres como para mujeres, sugiriendo que un aumento en el capital humano no necesariamente reduce la segregación.
En América Latina, el fenómeno de segregación ocupacional por sexo también es visible. El Centro Interdisciplinario de Estudios sobre el Desarrollo de Uruguay (Ciedur) analizó ocho países de la región —Brasil, Colombia, Costa Rica, Ecuador, El Salvador, Guatemala, México, Uruguay— en pos de cuantificarla para los años 2000 y 2015, utilizando los índices de disimilitud de Karmel y MacLachlan (km) y Duncan (id). Estas mediciones permiten establecer comparaciones entre la segregación ocupacional registrada en diferentes países, o en un mismo país en diferentes momentos.
Los resultados revelan el grado de segregación ocupacional en todos los países y sus tendencias entre el 2000 y 2015. Uruguay se mantuvo prácticamente igual (con un id de 0.54, km de 0.27), mientras que en Colombia y El Salvador se vio una reducción de ambos índices. No obstante, es válido mencionar que ambos eran los países con índices más altos en el 2000; sus valores en el 2015 indican mejoría (id de 0.50 y 0.59, km de 0.25 y 0.29, respetivamente), pero distan de escenarios de baja segregación. Finalmente, en Brasil, Costa Rica, Ecuador, Guatemala y México se visibilizan tendencias al alza en las medidas de segregación: salvo Ecuador (id y km de 0.22), todos los índices se mueven entre el rango de [0.44, 0.55] para el índice de Duncan, y [0.22, 0.26] para el índice de Karmel y MacLachlan (Espino & De los Santos, 2019).
Así mismo, el Banco de Desarrollo de América Latina (caf) exploró el vínculo entre segregación y brecha partiendo de la hipótesis de que, si hay una tendencia del sexo femenino a agruparse en determinados sectores de paga baja, surgirá naturalmente una brecha con los hombres, aun sin la existencia de discriminación al interior de cada ocupación. Si bien se menciona que para América Latina los estudios preexistentes suelen encontrar que la segregación ocupacional no es el factor con mayor impacto sobre la brecha, se itera el análisis utilizando un modelo de regresión e incorporando variables dummies por sector. Se estimó para tres franjas etarias (25-54 años, >15 años, 25-64 años), y para cada país, tomando luego un promedio no ponderado de los coeficientes estimados para obtener un estimador a nivel América Latina. Se evidenció que, controlando por sector, las brechas salariales se reducen, pero el efecto es menor al 15 %. De ese modo se concluye que la segregación ocupacional tiene relevancia, pero que también es importante entender la composición de sexo dentro de las ocupaciones, y no solo entre diferentes ocupaciones (Marchionni et al., 2019).
2. Metodología
Para estimar el impacto entre la proporción de mujeres por ocupación y el ingreso percibido se utilizarán cuatro modelos: regresión lineal múltiple (mcc), regresión lineal en dos etapas o variables instrumentales (iv), regresión cuantílica (qr) y regresión cuantílica bajo variables instrumentales (sivqr). En esta sección se presentan los marcos teóricos de cada modelo y las especificaciones econométricas de interés.
2.1. Desarrollo de la metodología econométrica
2.1.1. Modelo de regresión cuantílica
Los resultados tanto del modelo de regresión lineal múltiple, como el de mínimos cuadrados en dos etapas (variables instrumentales), proveen estimaciones promedio de los efectos de las covariables sobre la variable de interés. El modelo de regresión cuantílica permite obtener estimaciones sobre toda la distribución condicional de la variable dependiente, basándose en los estadísticos de orden.
El τ -ésimo cuantil condicional de la variable dependiente, dado X = x puede ser definido como 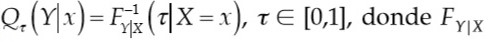 es la función de distribución acumulada condicional de Y. Qτ(Y|x) puede ser interpretado como el umbral tal que τ % de la masa de y está por debajo del mismo (Pouzo, 2020). Por ejemplo, la mediana condicional es la solución al problema de minimización:
es la función de distribución acumulada condicional de Y. Qτ(Y|x) puede ser interpretado como el umbral tal que τ % de la masa de y está por debajo del mismo (Pouzo, 2020). Por ejemplo, la mediana condicional es la solución al problema de minimización:

Eso significa que 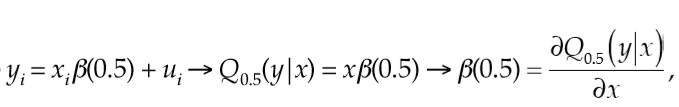 , es decir, los coeficientes de la regresión de la mediana no son más que el efecto marginal de un cambio de x sobre la medida condicional en la variable dependiente (Montes Rojas, 2020).
, es decir, los coeficientes de la regresión de la mediana no son más que el efecto marginal de un cambio de x sobre la medida condicional en la variable dependiente (Montes Rojas, 2020).
Extendido a todas las condiciones de orden, ∀ τ ∈(0.1) de interés, si definimos a q0( τ ) como el τ -ésimo cuantil de yi, entonces q0( τ ) resuelve el problema de minimización de la suma de los desvíos absolutos:
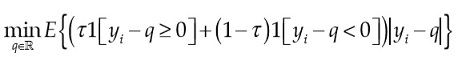
Donde 1[⋅] es la función indicadora que toma el valor 1 si el argumento entre corchetes es cierto, y 0 en caso contrario. La función:
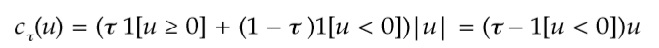
es conocida con el nombre de función de pérdida absoluta asimétrica, o check function, por su gráfica es similar a una marca de verificación.
2.1.2. Modelo de regresión cuantílica con VI suavizado (Smoothed IV quantile regression)
La habilidad de los modelos de regresión cuantílica para caracterizar el impacto heterogéneo de covariables en diferentes estadísticos de orden de la distribución de la variable de interés, provee muchas ventajas en aplicaciones económicas. Sin embargo, pueden existir problemas de endogeneidad que traen como resultado estimaciones inconsistentes (Chernozhukov & Hansen, 2005).
De la misma forma que el modelo de regresión lineal en dos etapas soluciona el problema de endogeneidad, el modelo de Smooth IV quantile regression (sivqr) incorpora instrumentos y optimiza una función objetivo, la diferencia es que este enfoque está basado en estimadores condicionales no paramétricos basados en kernels (Kaplan & Sun, 2016).
Partiendo del modelo estructural más simple, donde y = β 0 + β 1x + υ , β 0 y β 1 son constantes desconocidas, β1 cuantifica el efecto causal que tiene el regresor sobre la variable dependiente. Sin embargo, empíricamente, rara vez se ve que el efecto sea igual para toda la población. Ante este escenario, hay dos alternativas, o se permite que las diferencias sean capturadas por el error y se interpreta a β 1 como un promedio, o se trata de medir el efecto de la heterogeneidad.
Si se permite que todos los individuos tengan un efecto diferente, los coeficientes —que ahora son aleatorios, no fijos— pueden ser expresados como funciones determinísticas de un escalar inobservable u, tal que b0 = β0(u) y b1 = β1(u). Como no hay restricciones sobre β 0 y β1, la distribución de u puede ser normalizada a una uniforme: u ~ [0,1]. Las funciones β 0(⋅) y β 1(⋅) son desconocidas pero determinísticas: si se evalúan en un τ ∈ (0,1), β0( τ ) y β1( τ ) se convierten en dos constantes desconocidas, tal como eran β0 y β 1 en un principio. Por lo tanto, las diferencias entre individuos vienen caracterizadas por u, cada observación tiene su propio vector (y, x, u) donde y = β0(u) + β1(u)x, y β0(⋅) y β1(⋅) no son específicas a ningún individuo.
Uno de los supuestos necesarios para que el modelo estructural esté bien definido, es el de invariancia del ranking, u describe como el y de un individuo se rankea en la población, si todos tuviesen el mismo x: si u = 0.5, y sería la mediana, si u = 0.9, el individuo estaría en el percentil 90 % de y. Si todos mantienen el mismo ranking independientemente del x, se sostiene la propiedad de invariancia, aun si x es endógeno; si ese es el caso, se pueden estimar β0( τ ) y β 1( τ ) siempre que exista un instrumento z que correlacione con x, y que no correlacione con u.
La interpretación de los parámetros depende parcialmente de la invariancia del ranking: si es válida, β0( τ ) + β1( τ )x0 es el valor de y para un individuo cuyo ranking es u = τ , y donde x = x0. Esta es la función estructural del τ -ésimo cuantil sobre la distribución poblacional no condicionada de u ~ [0,1] (Kaplan, 2020).
Chernozukov y Hansen (2005) muestran cómo derivar condiciones de momento, usando instrumentos y notar que la definición de los momentos condicionales es análoga a la de variables instrumentales. Si υ ≡ y – β 0 – β1x, en variables instrumentales, las condiciones de momento son:
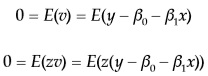
Para ivqr, las condiciones de momento son:
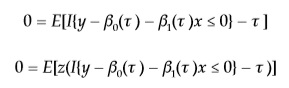
Donde I{⋅} es una función indicadora que toma el valor 1 si se cumple el argumento, 0 en caso contrario. La principal diferencia entre iv e ivqr es que, al tener una función indicadora, no existe una solución explícita de las condiciones de momento, ya que las mismas no son funciones diferenciables de los parámetros. Al desarrollar algebraicamente lo mencionado en los párrafos previos, para obtener β, partimos del siguiente modelo estructural:
y = χ ' β + u
Si los instrumentos son independientes del error estructural, entonces, por ley de expectativas iteradas (lei):
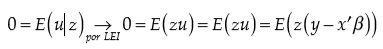
Si a esto le sumamos identificación exacta —las dimensiones de z y x son iguales—, obtenemos explícitamente el estimador de β :
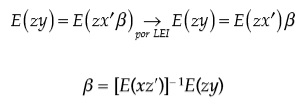
Ahora, si tuviésemos cuantiles en vez de la media, vale que condicional a los valores que toma z, la distribución condicional de u es 0:
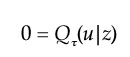
Por definición, el τ -ésimo cuantil de una distribución es el valor con probabilidad τ bajo ese corte, y se sostiene aun condicionando por z, entonces 0 = Q τ (u|z) es equivalente a:
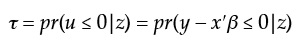
Al utilizar la función indicadora mencionada, se reemplaza la probabilidad por la esperanza de la función indicadora y se usa ley de expectativas iteradas (lei) para reescribir τ como:
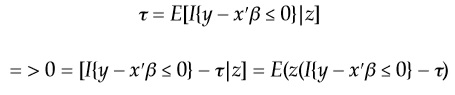
En este caso, se debe resaltar que β está dentro de la función indicadora, y no hay una solución explícita al problema de optimización. Como alternativa, Kaplan y Sun (2016) plantean reemplazar la función indicadora (no diferenciable) con una función similar “suavizada”, continua y diferenciable. Si se reemplaza I{ υ ≤ 0} por una función de υ —llamémosla I ~ ( υ )—, que en vez de decrecer discontinuamente de 1 a 0 (en υ = 0), decrece continuamente entre el rango de – 1 ≤ v ≤ 1, el problema se podría resolver numéricamente. Si a esta función “suavizada” le agregamos un ancho de banda h, tal que I ~ ( υ / h ) , permitimos que la función decrezca más rápido entre – h ≤ υ ≤ h . Finalmente, el estimador β ^ SIVQR surge de resolver el sistema de condiciones de momento “suavizadas”:
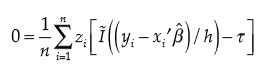
Donde:
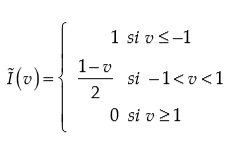
2.2. Fuente de información
La fuente primaria de información es la Encuesta Permanente de Hogares (eph) del indec, para un periodo de tiempo de cuatro años, desde el segundo trimestre del 2016 hasta el tercer trimestre del 2020. La eph se realiza todos los años brindando información trimestral, por lo que se dice que su periodicidad es permanente. Se lleva a cabo en hogares, entendiendo por hogar a individuos o grupos de personas que viven bajo un mismo techo y comparten sus gastos esenciales para vivir.
Los microdatos presentan distintas características observables de los individuos, tales como edad, sexo, estado civil, lugar de residencia, características educacionales, características de ingreso, entre otros.
De las bases de datos trimestrales del indec, se realizaron algunas modificaciones. En primer lugar, solo se considera a la población mayor de 18 años, y menor de 60 y 65 si el sexo es femenino y masculino, respectivamente. Por otro lado, se tuvieron en cuenta individuos que declararan que su ocupación principal pertenecía al sector público o privado. Y para evitar outliers, se descartaron las observaciones donde los individuos declararon trabajar más de 84 horas por semana en su ocupación principal —lo que arrojaría un total de 12 horas al día—.
La variable dependiente es una construcción que surge del monto de ingreso percibido por la ocupación principal. Sin embargo, para que sea comparable entre trimestres, se dividió dicha variable por la canasta básica de alimentos (cba) de cada trimestre y de cada región. Luego, para tener una medida del ingreso horario, se dividió el ingreso mensual real por la cantidad de horas mensuales trabajadas en la ocupación principal. Por último, se calculó el logaritmo de cada observación para suavizar su función de distribución.
Dado que se intenta comprobar si existe algún efecto de la cantidad de mujeres por ocupación en el ingreso horario percibido, la variable independiente que más importancia tiene en nuestro estudio es la proporción de mujeres por ocupación. Para crearla se utilizaron las variables ppo4b_cod y ppo4d_cod. La primera, codifica las ocupaciones de los individuos según el Clasificador de Actividades Económicas para Encuestas Sociodemográficas del Mercosur (caes) y la segunda, con el Código Nacional de Ocupaciones (indec, 2011). Utilizando ambos códigos se clasificó a los individuos en 47 ocupaciones (véase Anexo A). Finalmente, se calculó la proporción de mujeres en cada ocupación ( π j ) como:
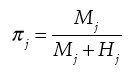
Donde Mj es la cantidad de mujeres en la ocupación j, mientras que Hjes la cantidad de varones en la ocupación j.
3.3 Especificación econométrica
Para este estudio se presenta el siguiente modelo de regresión:
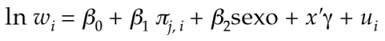
Donde ln w i es el logartimo del ingreso real horario, π j , i es la proporción de mujeres en cada ocupación j , sexo es una variable dicotómica que toma el valor 1 si el individuo es mujer, 0 si es hombre, mientras que x ' es un vector que incluye otras covariables —categoría ocupacional, nivel educativo, región, año de encuesta, edad y edad cuadrado—.
A priori la estimación por mínimos cuadrados clásicos puede presentar un problema de endogeneidad de la variable “proporción mujeres por ocupación”, debido a causalidad simultánea. Es decir, así como la ratio afecta a la variable dependiente, esta a su vez afecta a la ratio. Tener regresores endógenos en un modelo hará que la estimación por mínimos cuadrados clásicos esté sesgada, ya que una de las suposiciones de mcc es que no existe correlación entre una variable explicativa y el término de error. Para testear la existencia de endogeneidad se podría utilizar el test de Durbin–Wu–Hausman (véase Anexo B, tabla B1). En este caso, el p-valor es menor a nuestros niveles de significancia, por lo tanto, hay evidencia a favor de rechazar la hipótesis nula que la proporción de mujeres por ocupación es exógena. Por este motivo es necesario una estimación en dos etapas, utilizando variables instrumentales y aplicando el método de mc2e. Similar al trabajo de Clarhall (2011), el instrumento elegido es la proporción de mujeres por ocupación para el periodo 2011-2012. Por la relevancia de dicho instrumento, se realizó la prueba de significatividad individual, obteniendo evidencia que rechaza la hipótesis nula, a favor de la significatividad del coeficiente (véase Anexo B, tabla B2).
Por último, se realizan los modelos especificados para regresión cuantílica en cuantiles condicionales y regresión cuantílica con variables instrumentales suavizadas (Smoothed IV quantile regression). Como consideración, es de nota que no se presenta una prueba de Durbin–Wu–Hausman (dwh) para el caso de cuantiles. Existen varios enfoques sobre cómo suplantar dwh en estos casos, como los trabajos de Chernozhukov y Hansen (2006), y Kim y Muller (2013), pero computacionalmente son muy costosos y no hay paquetes estadísticos que lo calculen. Algunos trabajos empíricos como Arabsheibani, Murphy y Staneva (2010), reconocen esta limitación y usan dwh como un proxy.
3. Resultados
3.1. El caso argentino: una mirada del mercado laboral (2016-2020)
Utilizando información de la Encuesta Permanente de Hogares, podemos adentrarnos en la estructura del mercado laboral argentino. Partiendo de lo más general, en la figura 1 se presenta la pirámide poblacional de aquellos individuos que declararon estar ocupados, y la proporción de ocupados por sexo para el periodo de interés.1 En ambos casos, la mayor cantidad de individuos que declaran estar ocupados se encuentran entre los 25 y 50 años, pero para todas las franjas etarias la cantidad de mujeres que declaran estar ocupadas es menor —tendencia que se mantuvo estable en los últimos años—.
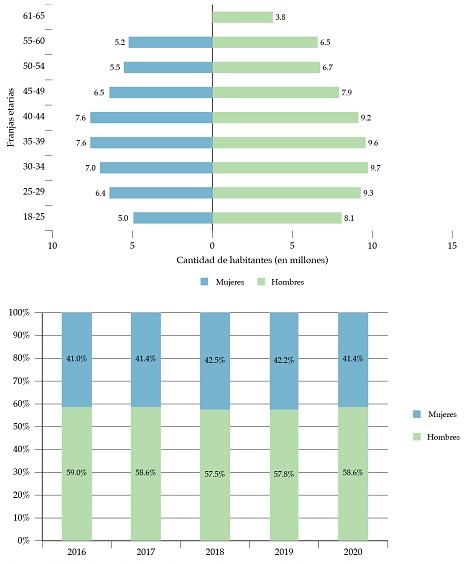
Se puede evidenciar que existe una predominancia de hombres ocupados, sin embargo, ¿acaso está tendencia se sostiene para las diferentes categorías ocupacionales? Dentro de los ocupados se definen cinco subgrupos: asalariados formales, informales, públicos y privados e independientes. En algunos ámbitos la proporción de hombres/mujeres es similar (± 5 %, como en el grupo de asalariados informales privados y de asalariados formales e informales públicos), pero en los formales privados e independientes se observan diferencias bastante importantes.
Es evidente que, salvo algunas excepciones, el mercado laboral argentino tiende a tener una predominancia masculina. No obstante, ¿se mantienen estas tendencias en todas las ocupaciones?, ¿es posible desagregar acorde al grado de feminización? Usando el Código Nacional de Ocupaciones y la Clasificación de Actividades Económicas para Encuestas Sociodemográficas, se separa a los ocupados en 47 grupos (véase Anexo A).
En la figura 2 se reporta la relación del percentil promedio del ingreso horario real y la proporción de mujeres por ocupación2 para las 47 ocupaciones, donde se observa una relación negativa en los ingresos en la ocupación principal, a medida que aumenta la proporción de mujeres.
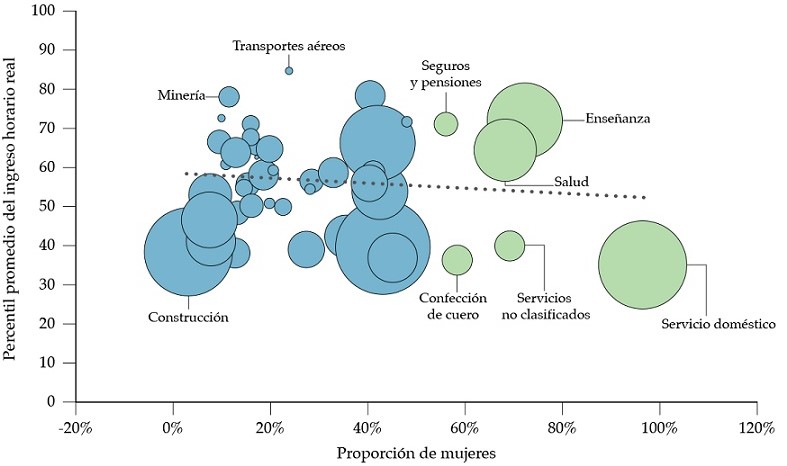
3.2. Resultados econométricos
En la tabla 1 se presentan los resultados de las estimaciones:
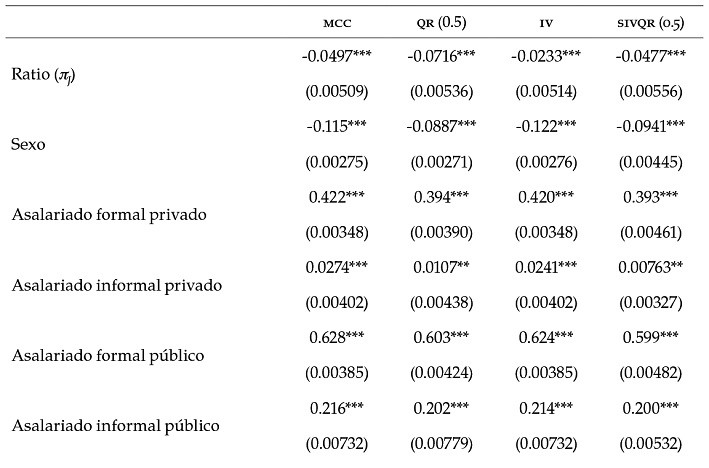
Los resultados de las estimaciones confirman nuestra hipótesis de la existencia de un efecto causal negativo de la proporción de las mujeres por ocupación sobre el ingreso horario promedio percibido. En el caso de mcc vemos que un cambio de 10 puntos porcentuales (p.p.) en la ratio de mujeres en la ocupación j, lleva a una caída promedio del salario del 0.50 %. Para el caso de mc2e, obtenemos un coeficiente de -0.0233: un cambio de 10 p.p. en la ratio de mujeres en la ocupación j, lleva a una caída promedio del salario de 0.23 %. Para el caso de la mediana condicional bajo regresión por cuantiles, obtenemos una caída de 0.72 %, mientras que, instrumentando con sivqr, la magnitud es menor: 0.48 %.
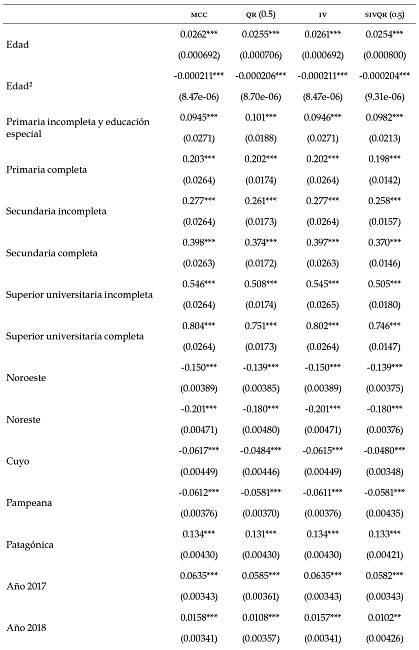
En relación con las covariables remanentes, en primer lugar, vemos que existe un efecto negativo y significativo para las mujeres, comparado a los hombres en el ingreso en promedio, las mujeres ganan entre un 11 y 12 % menos, por el hecho de ser mujer. Si lo vemos para la mediana, la magnitud es menor, pero sigue siendo negativa: entre un 8 y 10 %. Por otro lado, existe un efecto positivo en todos los tipos de categoría ocupacional sobre el ingreso, comparado con la categoría de independientes, al igual que con todos los niveles educativos, tomando como base el grupo sin instrucción.
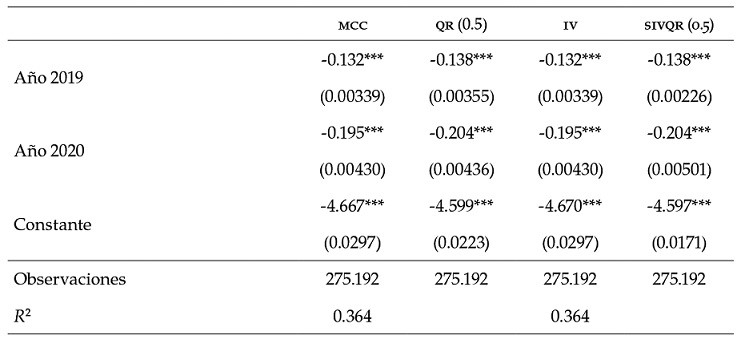
La edad también tiene un efecto positivo sobre el ingreso —intuitivamente podría estar relacionado con el nivel de experiencia, a mayor edad, más tiempo en el mercado laboral, y más calificación tienen los individuos—, pero su coeficiente al cuadrado es negativo, signo de que la edad podría tener un rendimiento decreciente —más experiencia aumenta el ingreso, pero los retornos marginales son cada vez menores—. También se observa que hay un efecto negativo sobre el ingreso de casi todas las regiones, tomando como base Gran Buenos Aires, la única excepción es Patagonia. Por último, vemos que para el 2017 y 2018 el efecto del paso de los años (tomando como referencia el 2016) tiene un impacto positivo sobre el ingreso, pero se invierte para el 2019 y 2020, potencialmente alineado con las condiciones económicas argentinas.
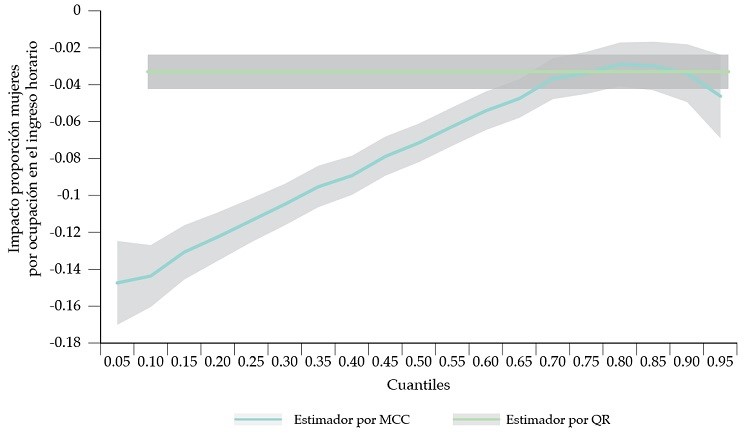
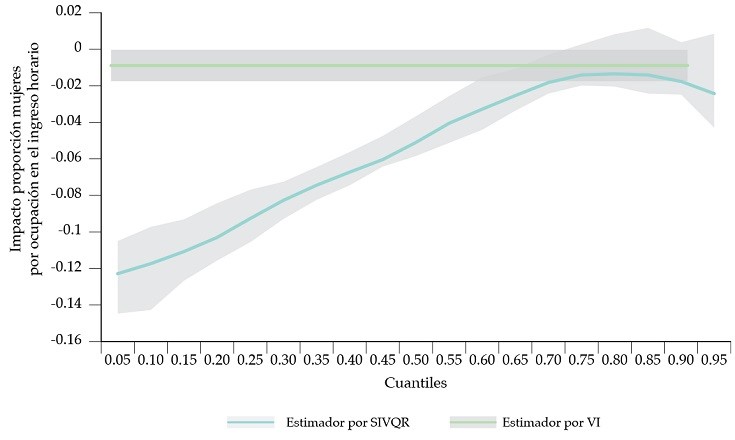
En las figuras 3 y 4 se puede visualizar cuáles fueron los resultados de las estimaciones del efecto de la proporción de mujeres por ocupación sobre el ingreso horario percibido, para todos los estadísticos de orden de interés con sus intervalos de confianza al 95 % vs. los resultados por mcc e iv.
Independiente del método de estimación implementado, todos los resultados muestran que existe un impacto negativo y significativo de la proporción de mujeres por ocupación sobre el ingreso. El valor agregado de las estimaciones por cuantiles condicionales es visibilizar que, dependiendo del ingreso percibido, varía la magnitud del efecto: en cuantiles condicionales más bajos, el efecto de la ratio de mujeres es mayor, alrededor de un 1.45 % de caída del ingreso cuando aumenta en 10 p.p. la proporción, contra un 0.45 % en el caso del cuantil más alto.
Conclusiones
La desigualdad por sexo en el mercado laboral es una cuestión de estudio desde hace aproximadamente 60 años en el ámbito global. Nuestro análisis quiere demostrar, a través del enfoque de la segregación ocupacional, que tal desequilibrio existe en el mercado argentino y se procede a cuantificar. A partir de los resultados obtenidos, vemos que ante un aumento de la proporción de mujeres en 10 p.p. para una ocupación determinada, el ingreso horario promedio de los trabajadores de tal ocupación disminuye en 0.50 %. Al hacer la estimación en dos etapas, para sortear el problema de endogeneidad por causalidad simultánea, se obtiene un valor del 0.23 %.
Sumado a esto, cuando se analiza el impacto en los diferentes cuantiles condicionales, se ve un efecto más fuerte sobre la proporción de individuos con salarios más bajos (-1.47 % y -1.44 % en los cuantiles que acumulan menor distribución del ingreso), mientras que la magnitud disminuye de forma gradual hasta -0.46 % en el cuantil extremo derecho. Los resultados persisten, aun sorteando la existencia de endogeneidad en los regresores: -1.23 % en el cuantil más bajo, -0.24 % en el superior.
Por lo tanto, hay evidencia estadísticamente relevante que avala nuestra hipótesis: la existencia de un efecto causal, robusto y negativo entre la proporción de mujeres en una ocupación y el ingreso horario real en el mercado laboral argentino. Pues no solo existe discriminación en el mercado laboral por el sexo en sí mismo, sino también por cómo se concentran los sexos en las distintas ocupaciones. Es decir, en promedio las mujeres ganan menos que los hombres, pero hombres en ocupaciones con mayoría de mujeres perciben menos ingreso que en otras ocupaciones con más presencia masculina. Y las mujeres, en ocupaciones con predominancia femenina tienen un doble efecto negativo en su ingreso, cuya magnitud es aún mayor en la población con menor acumulación de ingreso.
En definitiva, aproximarnos a la raíz de la brecha salarial a través de la segregación, es una perspectiva que explora las desigualdades salariales que enfrentan las diversas ocupaciones, por ser consideradas más femeninas o masculinas. Los resultados sirven, no solo para brindar evidencia empírica a las investigaciones preexistentes, sino también para enfatizar en el desarrollo de políticas de género, focalizando además de en el sexo, en el tipo de ocupación y en el nivel de ingresos. Sería interesante ver el efecto de implementación de políticas que fomenten la contratación de mujeres en ocupaciones con predominancia masculina —sobre todo en el sector privado, donde los datos indican que la presencia femenina es menor—, ya sea con subsidios o incentivos monetarios, aunque a largo plazo, se debería apuntar a tomar medidas que colaboren a deconstruir tanto el rol de la mujer como el del hombre en el mercado laboral. Ambos sexos resultan perdedores ante el encasillamiento cultural de uno u otro en los diferentes tipos de ocupaciones, al generarse preconceptos tanto en el empleado, como en el empleador a la hora de buscar trabajo y contratar a un individuo sobre otro.
Los cursos de acción posibles son múltiples, las estimaciones proporcionan una oportunidad para seguir desarrollando futuras investigaciones que apunten a profundizar la causa de dicha brecha y desigualdad por sexo en el mercado laboral. A su vez, evidencia la necesidad de seguir debatiendo esta problemática, a fin de ir minimizando las consecuencias económicas que se crean en el mercado laboral a partir de la segregación ocupacional y brindar políticas públicas que apunten a cerrar este desequilibrio existente.
Referencias
Arabsheibani, R., Murphy, P., & Staneva, A. (2010). Returns to education in four transition countries: Quantile regression approach. IZA Discussion Paper n.° 5210, 1-36. http://dx.doi.org/10.2139/ssrn.1686501
Blau, F. D., & Jusenius, C. (1976). Economists’ approaches to sex segregation in the labor market: An appraisal. Signs: Journal of Women in Culture an Society, 1(3, Part 2), 181-199. https://www.journals.uchicago.edu/doi/abs/10.1086/493286?journalCode=signs
Blau, F. D., & Kahn, L. (2017). The gender wage gap: Extent, trends, and explanations. Journal of Economic Literature, 55(3), 789-865. https://doi.org/10.1257/jel.20160995
Chernozhukov, V., & Hansen, C. (2006). Instrumental quantile regression inference for structural and treatment effect models. Journal of Econometrics, 132(2), 491-525. https://doi.org/10.1016/j.jeconom.2005.02.009
Chernozhukov, V., & Hansen, C. (2006). Instrumental quantile regression inference for structural and treatment effect models. Journal of Econometrics, 132(2), 491-525. https://doi.org/10.1016/j.jeconom.2005.02.009
Clarhall, J. (2011). Causal effects of occupational gender segregation and wages. University of Oslo.
Coverman, S. (1983). Gender, domestic labor time, and wage inequality. American Sociological Review, 48(5), 623-637. https://doi.org/10.2307/2094923
Del Río, C., & Alonso-Villar, O. (2010). Gender segregation in the spanish labor market: An alternative approach. Social Indicators Research, 98(2), 337-362. https://doi.org/10.1007/s11205-009-9548-0
Espino, A., & De los Santos, D. (2019). La segregación horizontal de género en los mercados laborales de ocho países de América Latina: implicancias para las desigualdades de género. Centro Interdisciplinario de Estudios sobre el Desarrollo de Uruguay; Organización Internacional del Trabajo; Programa de las Naciones Unidas para el Desarrollo. https://www.ilo.org/wcmsp5/groups/public/—-americas/—-ro-lima/documents/publication/wcms_715929.pdf
Hanson, S., & Pratt, G. (1991). Job search and the occupational segregation of women. Annals of the Association of American Geographers, 81(2), 229-253. https://doi.org/10.1111/j.1467-8306.1991.tb01688.x
indec. (2011). Clasificación de Actividades Económicas para Encuestas Sociodemográficas del MercOsur. indec. https://www.indec.gob.ar/ftp/cuadros/menusuperior/eph/caes_mercosur_1.0.pdf
indec. (2017). Encuesta Permanente de Hogares (epH). indec. https://www.indec.gob.ar/bases-de-datos.asp
Kaplan, D. (2020). sivqr: Smoothed iv quantile regression. The Stata Journal, 2, 1-24. http://web.missouri.edu/~kaplandm/pdfs/sivqr.pdf
Marchionni, M., Gasparini, L., & Edo, M. (2019). Brechas de género en América Latina. Un estado de situación. caf: Banco de Desarrollo de América Latina. http://scioteca.caf.com/handle/123456789/1401
Pouzo, D. (2020). Introduction to Quantile Regression Models. Microeconometría II (pp.3-12). Universidad Torcuato Di Tella.
Kaplan, D., & Sun, Y. (2016). Smoothed estimating equations for instrumental variables quantile regression. Econometric Theory, 33(1), 105-157. https://doi.org/10.1017/S0266466615000407
Kim, T., & Muller, C. (2013). A Test for Endogeneity in Conditional Quantiles. Aix-Marseille School of Economics, 1-17. https://halshs.archives-ouvertes.fr/halshs-00854527/
Organización Internacional del Trabajo. (2015). Informe Mundial sobre Salarios 2014/2015: Salarios y desigualdad de ingresos. Organización Internacional del Trabajo. https://www.ilo.org/global/publications/books/WCMS_343034/lang—es/index.htm
Okamoto, D., & England, P. (1999). Is there a supply side to occupational sex segregation?. Sociological Perspectives, 42(4), 557-582. https://doi.org/10.2307/1389574
Montes Rojas, G. (2020). Quantile Regression. Universidad Torcuato Di Tella. http://gabrielmontes.com.ar/Quantile%20regression.pdf
Reskin, B. (1993). Sex segregation in the workplace. Annual Review of Sociology, 19(1), 241-270. https://doi.org/10.1146/annurev.so.19.080193.001325
Anexos
Anexo A


Anexo B. Test de modelos econométricos


Notas
1
Se presenta información de población económicamente activa: hombres de 18 a 65 años, mujeres de 18 a 60 años.
2
El tamaño de la burbuja varía acorde a la cantidad de ocupados totales en la ocupación, y aquellas de color violeta son las ocupaciones con mayoría femenina.
Notas de autor
Autor de correspondencia. Dirección: Caseros 2241, San Martín, Buenos Aires, Argentina



