

Banks in Colombia: How Homogeneous Are They?*
Bancos en Colombia: ¿Qué tan homogéneos son?
Bancos na Colômbia: Que tão homogêneos são?
Banks in Colombia: How Homogeneous Are They?*
Revista de Economía del Rosario, vol. 23, no. 2, 2020
Universidad del Rosario
Received: 11 june 2019
Accepted: 15 january 2020
Additional information
To quote this article: León, C. (2020). Banks in Colombia: How Homogeneous Are They? Revista de Economía del Rosario, 23(2), 1-42. https://doi.org/10.12804/revistas.urosario.edu.co/economia/a.9180
Abstract:
In complex systems, homogeneity has been documented as a source of fragility. Likewise, in the financial sector, it has been documented as a contributing factor for systemic risk. We assess homogeneity in the Colombian case by measuring how similar banks are regarding the structure of their overall financial statements, and their lending, investment, and funding portfolios. Distances among banks and an agglomerative clustering method yield the hierarchical structure of the banking system, which exhibits how banks are related to each other based on their financial structure. The Colombian banking sector displays homogeneous features, especially among the largest banks. Also, it seems size is a crucial determinant in the banking sector’s hierarchical structure. Results are robust to a principal component analysis feature selection procedure that reduces the dimensionality of the dataset. Results enable studying to what extent the banking sector is homogeneous, to identify banking firms that have a(n) (un)common financial structure, and, thus, to better examine systemic risk. jel classification: G21, C38, L22, L25.
Keywords: Clustering, banks, diversity, systemic risk, machine learning.
Resumen:
La homogeneidad, entendida como la falta de diversidad, es una fuente de fragilidad en sistemas complejos. Del mismo modo, la homogeneidad del sistema financiero ha sido documentada como un factor determinante del riesgo sistémico. En este documento se evalúa la homogeneidad en el caso colombiano, para lo cual se mide qué tan similares son los bancos según la estructura de sus estados financieros generales, así como de sus portafolios de cartera, de inversiones y de pasivos. La similitud entre bancos y una metodología de agrupamiento por aglomeración arrojan la estructura jerárquica del sistema bancario, la cual muestra cómo los bancos se relacionan entre ellos de acuerdo con su estructura financiera. El sector bancario colombiano muestra homogeneidad, en especial entre los bancos de mayor tamaño. Así mismo, es evidente que el tamaño es un factor importante en la estructura jerárquica de este sector. Los resultados son robustos a partir de un procedimiento de selección de variables basado en análisis de componentes principales, el cual reduce la dimensionalidad y redundancia de la base de datos. Los resultados permiten estudiar qué tan homogéneo es el sistema bancario, así como identificar aquellas instituciones bancarias que tienen una estructura financiera común (particular) y, por lo tanto, permiten estudiar de mejor manera el riesgo sistémico. Clasificación jel: G21, C38, L22, L25.
Palabras clave: agrupamiento, bancos, diversidad, riesgo sistémico, aprendizaje automático.
Resumo:
A homogeneidade, entendida como a falta de diversidade, é uma fonte de fragilidade em sistemas complexos. Da mesma forma, a homogeneidade do sistema financeiro tem sido documentada como um fator determinante do risco sistémico. Neste documento se avalia a homogeneidade no caso colombiano, para o qual se mede que tão similares são os bancos segundo a estrutura de seus estados financeiros generais, assim como de seus portfólios de carteira, de inversões e de passivos com o público. A similitude entre bancos e uma metodologia de agrupamento por aglomeração registam a estrutura hierárquica do sistema bancário, a qual mostra como os bancos se relacionam entre eles de acordo com sua estrutura financeira. O setor bancário colombiano mostra homogeneidade, em especial entre os bancos de maior tamanho. Também, é evidente que o tamanho é um fator importante na estrutura hierárquica do setor bancário. Os resultados são sólidos a um procedimento de seleção de variáveis baseado em Análise de Componentes Principais, o qual reduz a dimensionalidade e redundância da base de dados. Os resultados permitem estudar que tão homogêneo é o sistema bancário, assim como identificar aquelas instituições bancárias que têm uma estrutura financeira comum (particular) e, portanto, permitem estudar de melhor maneira risco sistémico. Classificação jel: G21, C38, L22, L25.
Palavras-chave: agrupamento, bancos, diversidade, risco sistémico, aprendizagem automático.
Introduction
Complexity and homogeneity have been pinpointed as two defining but potentially problematic features of financial systems (see Haldane, 2009; Landau, 2009; Farmer et al., 2012). The financial system’s complexity refers to the many, intricate, and multi-dimensional connections among numerous adaptive financial institutions (see Sornette, 2003; Haldane, 2009; Landau, 2009). Homogeneity refers to the lack of diversity among financial institutions, presumably due to some form of uniform diversification (see Beale et al., 2011) or herding (see Sornette, 2003), which has resulted, for example, in similar balance sheets and risk management practices, common trading strategies, and correlated positions and returns (see Rebonato, 2007; Brown et al., 2009; Haldane, 2009; Haldane & May, 2011; Goodhart & Wagner, 2012). Together, complexity and homogeneity predispose financial systems to abrupt changes, even from small shocks (Haldane, 2009).
Our aim in this paper is examining similarity among Colombian banks by means of implementing agglomerative clustering techniques on a particularly granular decomposition of their financial statements (i.e., balance sheet and income statement), comprising more than 3000 different features (i.e., accounts) for each bank in a given period. Additionally, we measured similarity in the asset and liability sides of their financial structures by examining their lending, investment, and funding portfolios, which may be deemed as the three most interesting sections of their core banking functions.
Results suggest that the Colombian banking sector displays some degree of homogeneity that varies with the portfolio under examination. They also suggest that the distance among most contributive banks tends to be rather low. The lending, investment, and funding portfolios of the two largest banks by asset size are exceptionally similar. Also, it is apparent that size is a crucial determinant in the hierarchical structure of the banking sector. Results are robust to a principal component analysis feature selection procedure that reduces the dimensionality of the dataset.
Hence, results enable to determine to what extent the banking sector is homogeneous, to identify banking firms that have a(n) (un)common financial structure, and, thus, to better examine systemic risk.1 However, conclusions related to systemic risk and financial stability are conditional on unexplored factors, such as Colombian banking sector complexity, banks’ individual soundness, and higher dimensions of diversity.
The homogenization of financial institutions has intricate implications for the stability and efficiency of the financial system (Wagner, 2008). Literature has highlighted the importance of assessing and monitoring homogeneity in the financial sector, especially after the global crisis, that started circa 2007. For instance, as stated by Haldane and May (2011), in the run-up to the crisis and pursuit of diversification, banks’ balance sheets and risk management became increasingly homogeneous. Likewise, as pinpointed by Caccioli et al. (2014), common asset holdings and the related spiral effects have been the primary vector of contagion in the global financial crisis. It has been shown that clustered asset structures (i.e., groups of banks holding similar asset portfolios) entail higher systemic risk when bad information about banks’ future solvency arrives in the economy, whereas in unclustered structures default is more dispersed (Allen et al., 2012). Also, regarding the liability side of banks, by raising funds from similar sources, the financial system as a whole becomes vulnerable to disruptions in funding markets (Goodhart & Wagner, 2012). All in all, as put forward by several authors (Huang et al., 2013; Zhao et al., 2013; Caccioli et al., 2014; Aymanns & George, 2015), homogeneity, either in the form of overlapping portfolios or sharing similar financial positions, constitutes one of several contagion channels —along with counterparty and liquidity roll-over risk exposures—. Further, as reported by Elliot et al. (2014), Caccioli et al. (2014), and Roncoroni et al. (2019), the relation between homogeneity and financial stability is non-linear and context dependent.
Accordingly, the International Monetary Fund (2007) has stated that policymakers should recognize that a diversity of market participants is more suitable for market stability. Beale et al. (2011) have suggested that regulators may wish to promote systemic stability by incentivizing a more diverse diversification among banks. Haldane and May (2011) have emphasized that the objective of the regulatory community should be to give much greater prominence to the financial sector’s systemic diversity. Finally, Goodhart and Wagner (2012) have suggested that steps towards a safer financial system should not ignore the lack of diversity across financial institutions. Then, following Beale et al. (2011), regulators should pay attention to the average distance between banks as a measure of the financial system’s diversity and, thus, as an essential observable feature of systemic risk. In this vein, as liquidity spirals and common-shocks tend to be more likely and intense when financial institutions share similar portfolio positions and financial structures, monitoring similarity dynamics may help to identify systemic risk build-up.
Empirical related literature, devoted to measuring and examining the homogeneity in banking systems, is not abundant and has recently surfaced. Pool et al. (2015) measured the overlapping (i.e., similarity) of mutual funds managers’ stock portfolios, but focused on studying whether the social interaction of those managers may explain such overlap. Fricke (2016) examined the dynamics of homogeneity for Japanese banks’ loans portfolio from 1996 to 2013. Cai et al. (2017) studied the similarity of banks by measuring the one between their syndicated loan portfolios in the United States’ from 1989 to 2011. Our work is closely related to that of Fricke (2016) and Cai et al. (2017), but we contribute to the literature by implementing an agglomerative clustering technique to identify the groups of banks that may be regarded as particularly similar, and by using an unusually granular set of financial statements.
Some limitations are worth noticing. We limit our scope to banks because they are the most prevalent type of financial institution in related literature. As banks account for about 76 % of all financial institutions’ assets in the Colombian case, our results are representative. Also, due to some limitations on the extension of the datasets available, we restricted our examination to 2016’s average monthly financial statements.2 Moreover, although the dataset provides a particularly granular decomposition of banks’ financial statements that exceed the standard supervisory analysis, our exercise is unable to explore higher dimensions of banks’ financial position, such as the identity, industry, or geographical location of lenders and borrowers, which may be crucial to supplement the assessment of homogeneity across banking institutions. Finally, an explanatory or causal model of homogeneity is not intended.
Complexity and Homogeneity in Financial Systems
Complexity has been related to the existence of a system with a large number of elements that interact in a non-simple (i.e., non-linear) way, in which the whole is more than the sum of its parts (Simon, 1962). Similarly, Arthur (1999) pinpoints that all studies on complexity are systems with multiple elements adapting or reacting to the pattern these elements create.3
Financial systems’ complexity has no single definition and is difficult to measure (Gai et al. 2011). Yet, some distinctive features of financial systems’ complexity are rather evident (see, Arthur, 1999; Sornette, 2003; May et al., 2008; Landau, 2009; Haldane, 2009; León et al., 2012; Farmer et al., 2012): first, the large number of financial institutions (i.e., the elements of the system); second, financial institutions’ numerous, intricate, and somewhat opaque connections across several dimensions (i.e., markets, financial products, jurisdictions), which may take many forms, such as bilateral exposures (i.e., Bank A lends Bank B), payments (i.e., Bank A transfers funds to Bank B), common exposures (i.e., both Bank A and Bank B hold a bond issued by Firm C), or ownership relations (i.e. Bank A is the holding of Bank B), and third, financial institutions react with strategy and foresight by considering outcomes that might result as a consequence of the behavior they might undertake; that is, elements are adaptive. Fourth, the size of an event and its consequences may be unrelated, with modest events triggering disproportionally large changes (i.e., the US sub-prime crisis triggering the 2007-2008 global financial crisis). As highlighted by Lo (2011), the once simple and almost boring banking business (i.e., accepting deposits, paying interest, and making loans) has turned complex (i.e., spanning many markets, business, countries, and financial instruments) thanks to competition, deregulation, globalization, population growth, and technological and financial innovation.
Homogeneity has been related to the lack of diversity among the elements of a system. In turn, contemporary financial systems’ homogeneity is related to the sharp loss of diversity among financial institutions. Correspondingly, as emphasized by Goodhart and Wagner (2012), financial institutions —in particular very large ones— have become very similar to each other. From a behavioral viewpoint, herding and imitation in financial markets (see, Sornette, 2003) may be enduring factors behind this lack of diversity. However, there has been a recent severe loss in diversity, which has resulted from an extensive pursuit-of-return, uniform risk management tools, extreme spread of risk management best practice, consolidation, deregulation, disintermediation, and innovation (see, Rebonato, 2007; Wagner, 2008; Haldane, 2009; Goodhart & Wagner, 2012). Reduced diversity is apparent in homogenized financial sector balance sheets and risk management practice, and in financial institutions’ similar trading strategies, and correlated positions and returns (see, Rebonato, 2007; Brown et al., 2009; Haldane, 2009; Haldane & May, 2011; Goodhart & Wagner, 2012).
Beale et al. (2011) suggest that the recent lack of diversity may be driven by a uniform diversification process, which results in a state of the banks maximally herding together in the sense of adopting the same set of exposures by adopting common diversification strategies. In such a process, financial institutions diversify their risks and lower their own failure probability, at the expense of increasing the failure probability of the system as a whole (see, Wagner, 2008; 2010; May & Arinaminpathy, 2010; Ibragimov et al., 2011; Haldane & May, 2011; Fricke, 2016). That is, although diversification may be good for individual institutions, it can create dangerous systemic effects, and as a result, financial contagion gets worse with too much diversification (Caccioli et al., 2014). In this line, many banks diversifying in similar ways make joint failures more likely (Beale et al., 2011) because diversification makes the banks more similar to each other by exposing them to the same risks (Wagner, 2010). Also, when a large number of financial intermediaries choose the same investment strategy (i.e., their portfolios are very similar) the financial system as a whole becomes vulnerable to common shocks (Aymanns & George, 2015), and the lack of opposite positions can give rise to extreme price movements (Farmer et al., 2012). A stable financial system needs a diversity of views on risks that are competing with each other (Goodhart & Wagner, 2012).
The perils related to homogeneity are well known to complex systems’ literature. From a general viewpoint, Anderson (1999) highlights that partially connected systems (i.e., nonhomogeneous) are less unstable as the behavior of a particular agent depends on the behavior (or state) of some subset of agents in the system.
Financial systems’ systemic risk surging from homogeneity may be portrayed as a bipartite network (see, Zhao et al., 2013; Huang et al., 2013; Caccioli et al., 2014). A bipartite network is a graph with two groups of elements, in which linkages are inter-group only. In the financial systems’ base case, the two groups are financial institutions and assets (or liabilities, industries, etc.), in which a link exists between a bank and an asset when the bank has the asset in its portfolio, whereas no links between banks or assets exist.4
In it, risk propagates bidirectionally between assets and banks, and may be transmitted from one bank to another via a shared set of assets, and from asset to asset via a common set of holders. For instance, a sharp decline in the price of an asset may force a bank into a clearance sale of its portfolio that may further push asset prices downwards, therefore affecting other banks and other assets in a spiral of sales and descending prices. Intuitively, although banks have attained maximal diversification in the completely interconnected case portrayed in panel a. of figure 1, the spiral of sales and descending prices should be pronounced because all banks are linked by means of their common holding of assets (i.e., they are homogeneous). On the other hand, a weakly connected bipartite network (panel c.) should be immune to the aforementioned spiral effect, whereas a partially interconnected bipartite network (panel b.) should be affected in a limited manner. In this vein, as in a weakly connected system the short-run behavior of each of its components is approximately independent of the other components (Simon, 1962), avoiding financial system’s portfolio homogeneity allows for an advantageous degree of independence in the system, and a lower incidence of systemic risk and financial instability.
Strogatz (2003) suggests that there is a connection between the homogeneity of elements in a system and the latter’s propensity to lock in a potentially unstable state in which all elements act in a synchronized manner. And, by means of analogy, ceteris paribus, the more homogeneous financial institutions are, the more prone the financial system is to instability (Strogatz, private communication). Likewise, Wagner (2008) and Goodhart and Wagner (2012) suggest that a more homogeneous financial system means that contagion effects are likely to be more pronounced as a failure of one institution is then more likely to occur at times when other institutions are under stress.
Accordingly, in the spirit of Simon (1962) and Anderson (1999), systems’ fragility may be mitigated by allowing more heterogeneity among its elements. Hence, with financial stability in view, literature after the global financial crisis agrees on advising financial authorities to avoid financial institutions’ homogeneity by means of fostering financial markets’ diversity. For instance, Haldane and May (2011) assert that in rebuilding and maintaining the financial system, the systemic diversity objective should probably be given much greater prominence by the regulatory community. Likewise, to avoid the uniform diversification problem and its harmful consequences, regulators may wish to give banks incentives to adopt differentiated strategies of diversification (Beale et al., 2011). Or, as suggested in Allen et al. (2012) and Wagner (2010), from a systemic viewpoint, it may be optimal to limit or discourage diversification.
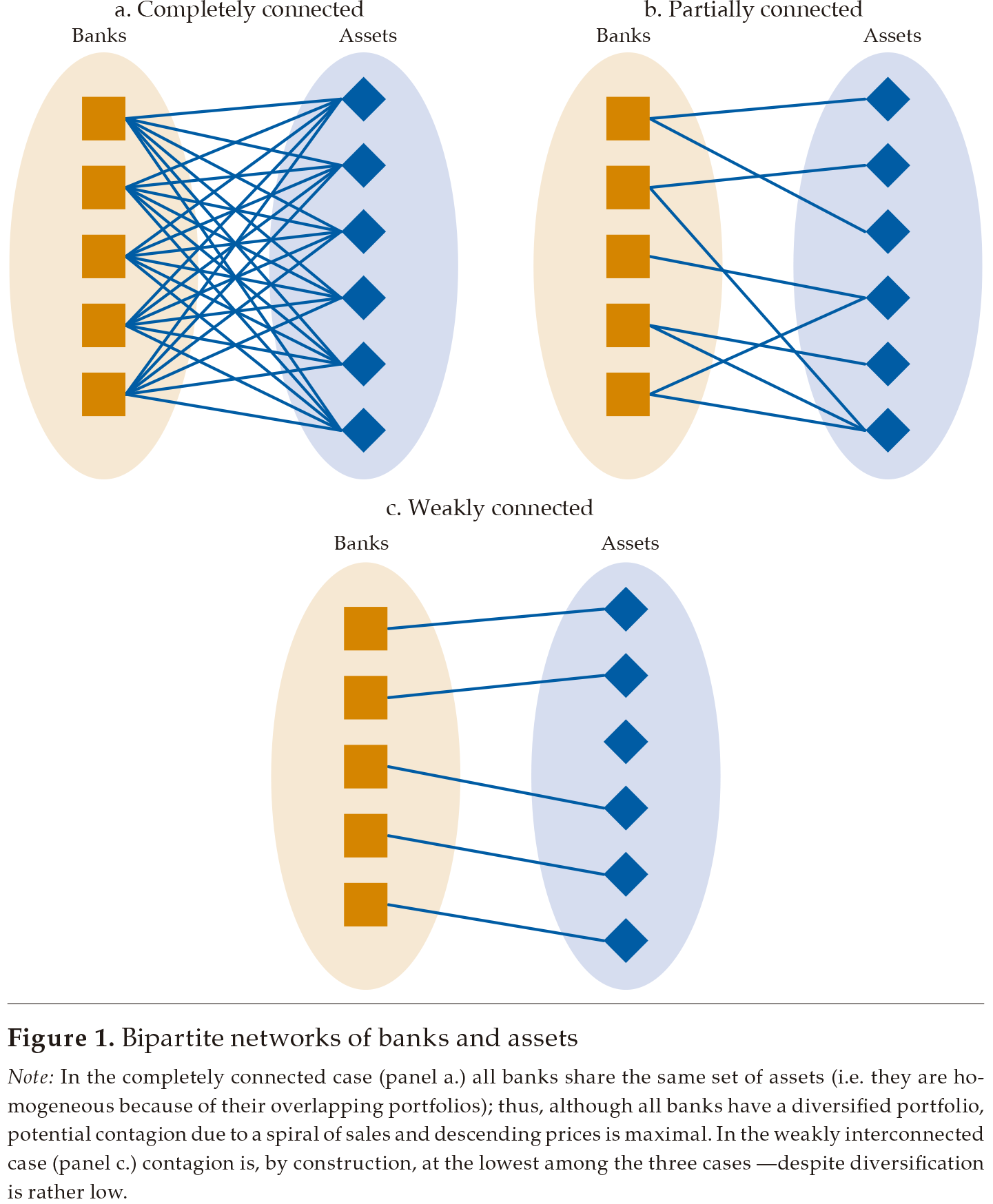
Note: In the completely connected case (panel a.) all banks share the same set of assets (i.e. they are homogeneous because of their overlapping portfolios); thus, although all banks have a diversified portfolio, potential contagion due to a spiral of sales and descending prices is maximal. In the weakly interconnected case (panel c.) contagion is, by construction, at the lowest among the three cases —despite diversification is rather low.
However, recent literature argues that the relation between homogeneity and systemic risk is a compound one. For example, Elliot et al. (2014) find a non-monotonic relation between diversification and cascades in financial networks. They find that diversification initially allows contagion by extending connections, but as diversification increases, it insures against failures; their results show that not only the level of diversification but the network structure determines the extent of contagion. Further, based on a stylized financial network model, Caccioli et al. (2014) report that the relation among the diversification and instability is non-monotonic and dependent on the leverage of financial institutions. That is, below some levels of leverage, financial networks are always stable irrespective of the diversification of overlapping portfolios; for some others, global cascades are very unlikely but catastrophic when they occur. Similarly, from an empirical perspective, Roncoroni et al. (2019) identify a non-linear relationship between diversification, shock size, and losses due to interbank contagion. Roncoroni et al. (2019) show that total contagion losses may be larger in a banking system with fully diversified exposures that in a concentrated one. Also, they find that a diversified network of financial linkages provides a better cushion for small-sized shocks, whereas a more diversified one propagates large shocks.5 Therefore, as the relation between homogeneity and financial networks stability is non-linear and context-dependent, authorities targeting the homogeneity of financial systems should be aware of the complexities involved.
Agglomerative Clustering6
Under the assumption that the data represents features that would allow distinguishing one group from another, a clustering procedure organizes a set of data into groups of observations (i.e., clusters) that are more similar to each other than they are to those belonging to a different group (Martínez et al., 2011). The main concern in clustering is to reveal the organization of patterns into “sensible” groups, which allows discovering similarities and differences and deriving useful conclusions about them (Halkidi et al., 2001).
As the clustering algorithm discovers by itself how the data may be organized, a clustering problem is considered an unsupervised machine learning problem (see Sumathi & Sivanandam, 2006).
In agglomerative clustering methods, we start with . groups (one observation per group) and successively merge the two most similar groups until we are left with one group only (Martínez & Martínez, 2008).7 The result of agglomerative clustering methods is a hierarchical structure that represents how observations relate to each other based on their cross-section similarities. The more similar their features, the closer they are in the hierarchy. The resulting structure is constrained to be hierarchical because the groups or clusters can include one another, but they cannot intersect (Witten et al., 2011).
The hierarchical classifications produced by agglomerative clustering are represented by a two-dimensional diagram known as a dendrogram or tree diagram, which illustrates the successive merges made at each stage of the procedure (Everitt et al., 2011). As the resulting hierarchy contains the entire topology of the observations’ grouping, it allows unveiling how the data is classified as the number of groups varies, from a single group to m groups, or vice versa.
The agglomerative clustering key is the selection of a dissimilarity measure. Distances are used as measures of dissimilarity, in which small (high) values correspond to observations that are close (distant) to (from) each other. Let xiwbe the w-th feature (i.e., the w-th item in the financial statement) of the i-th observation (i.e., the i-th bank), the most commonly used measure of distance between two banks, i and j, is their Euclidean distance, dij : 8
 [1]
[1]The similarity between two banks, i and j, as in [1], is calculated using all the features or accounts in the financial statements. The distance between two banks (i and j) is ultimately determined by the sum of those between i and j for each w-feature. If all w-accounts, in the financial statements, are strictly the same for two banks, i and j, then dijequals 0. Also, as a byproduct of the square of differences, dij equals dij (i.e., the dissimilarity between two banks is symmetric). Finally, regarding a third bank g, the distance between i and j, dij, should be lower or equal than the sum of distances dig and dgj(i.e., dij ≤ dig + dgj).
If there are n banks, the pairwise dissimilarity between them is presented as a n × n square matrix, which is commonly known as an interpoint distance matrix. Let D be an interpoint distance matrix based on a Euclidean distance, D is squared and symmetrical:
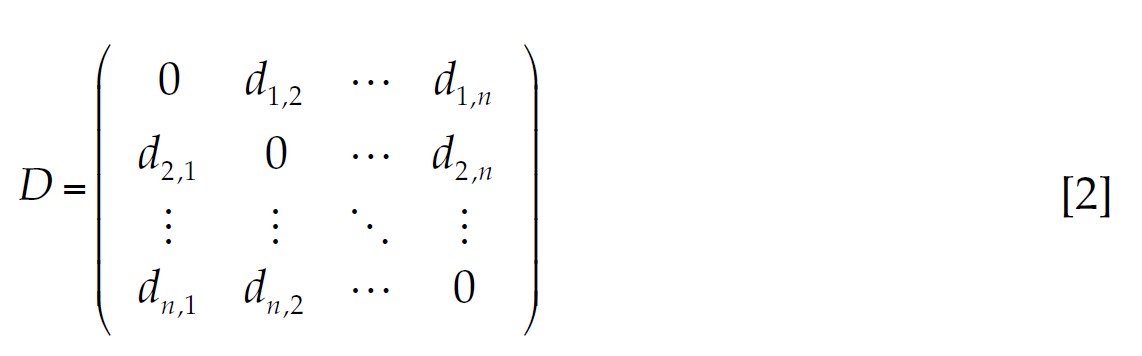 [2]
[2]In agglomerative clustering methods, we start with m groups (one observation per group) and successively merge the two most similar groups (i.e., the less distant) until we are left with one group only. As expected, the similarity criterion for merging groups is based on distance. However, measuring the distance between groups comprising several observations is different from measuring the distance between individual ones.
The way the distance between groups or clusters is calculated is known as the linkage method. Several linkage methods are available (see Everitt et al., 2011; Martínez et al., 2011).9 The simplest method is single-linkage (also known as nearest neighbor method), which uses the smallest distance between two observations pertaining to two different groups. Complete linkage (also known as furthest neighbor method) consists of using the maximum distance between two observations pertaining to two different groups. Average linkage uses the average distance from all observations in a group to all observations in another group. Centroid linkage measures the distance between clusters as the distance between the means of observations in each group (i.e., between the average observation of each cluster).
Figure 2 illustrates how these four basic linkage methods work in the case of two clusters, each one containing three observations. The discontinuous lines illustrate how the distance is calculated in each case.
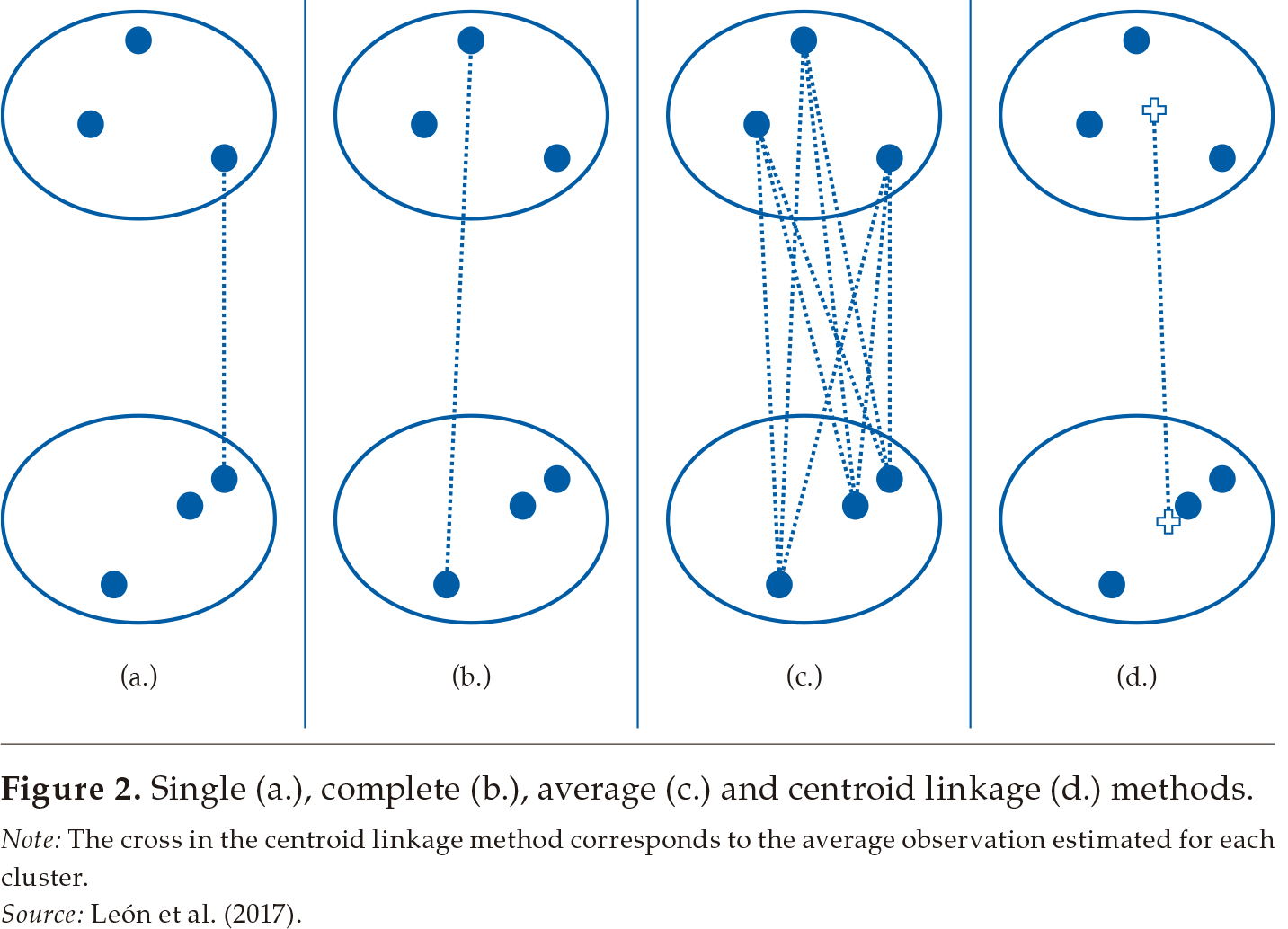
Note: The cross in the centroid linkage method corresponds to the average observation estimated for each cluster.
Ward (1963) realized that the linkage problem could be better described with an objective function that minimizes the loss of information caused by merging two groups into a single one. Ward’s choice for such objective function is the variance of distances among observations in a group (i.e., the sum of squares of distances within a group); hence, it is also known as the minimum variance method.
Each linkage method has its own shortcomings (see Martínez et al., 2011; Everitt et al., 2011). The choice of a linkage method should pursue the validity of the clustering solution. Such validity is commonly assessed by measuring how compact and separated the clusters are. As in Halkidi et al. (2001), clustering methods should search for clusters whose members are close to each other (i.e., compact) and well-separated. A widely used clustering validity criterion is the Calinski and Harabasz (1974) clustering validity index, which is the ratio of the between-cluster distance sum of squares (i.e., separateness) to the within-cluster distance sum of squares (i.e., compactness). The larger the index, the better the clustering solution.
The Data
We used the 2016’s average monthly financial statements for each bank. We focused on banks because they are the most prevalent type of financial institution in related literature, and they are the largest contributors to financial systems’ asset size (i.e., about 76 %). Also, as there are 25 banks in the sample, working on banks instead of the entire universe of financial institutions (about 150) enabled us to make a clearer visualization and analysis. The identity of banks was not disclosed.
Each financial statement in our dataset comprises 3063 features or attributes of banks, corresponding to six-digit filtering of statements reported to the Colombian Financial Superintendence under International Financial Reporting Standards (Ifrs). These 3063 features are continuous variables, all in monetary values (i.e., in Colombian pesos) that pertain to six different categories: assets (837), liabilities (575), equity (112), operational income (442), expenses (713), and disclosure (384).
Unlike traditional (i.e., summarized) financial statements, our dataset is particularly granular. Besides, not only our datasets include granular data on assets, liabilities, equity, income, and expenses, but they also comprise detailed data on banking firms’ loan portfolios (i.e., classified by type of loan, days of delinquency, and type of collateral), write-downs by type of loan, and received assets, among others. Hence, it is fair to state that the dataset used to calculate the similarity among banking firms is unusually detailed and comprehensive.
Three major portfolios may be extracted from financial statements, namely the investment portfolio (145 features), lending portfolio (111), and the funding portfolio (139).10 The investment portfolio and the lending portfolio pertain to the asset side of the financial statements, and they contribute to 18.62 and 67.25 % of banks’ assets, respectively. The funding portfolio pertains to the liability side, and it contributes to 86.11 % of banks’ liabilities. As not only these three portfolios account for most of the assets and liabilities of banks, but also correspond to their core banking activities, examining how similar banks are at the portfolio level is of utmost importance.
As usual, in order to avoid issues related to differences in scale or dispersion of data (see, Martínez et al., 2011), series are transformed (i.e., standardized) before calculating the distance dij as in [1]. This is done by means of subtracting their corresponding mean and dividing by their corresponding standard deviation, as in a customary z-score. After this transformation, the mean and standard deviation of financial statements for each banking firm are 0 and 1, respectively. Monetary values of financial statements and differences in scale are avoided; thus, the size of each banking firm is not considered a feature in the agglomerative clustering procedure. This is particularly convenient in our case because we are interested in determining how homogeneous banking firms are based on the similarity of their financial structure, not on their size. Further, as will be clear below, standardizing the series as in a z-score is particularly convenient because we can transform distances into correlations in a straightforward manner.11
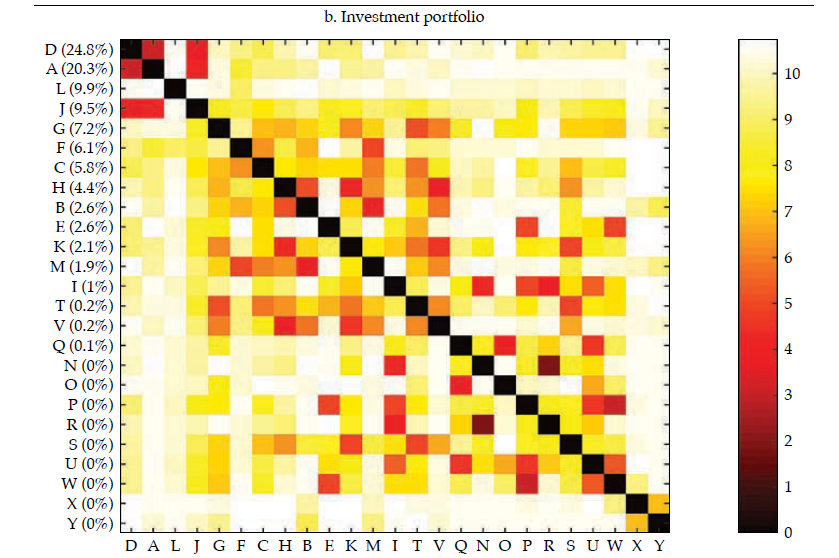
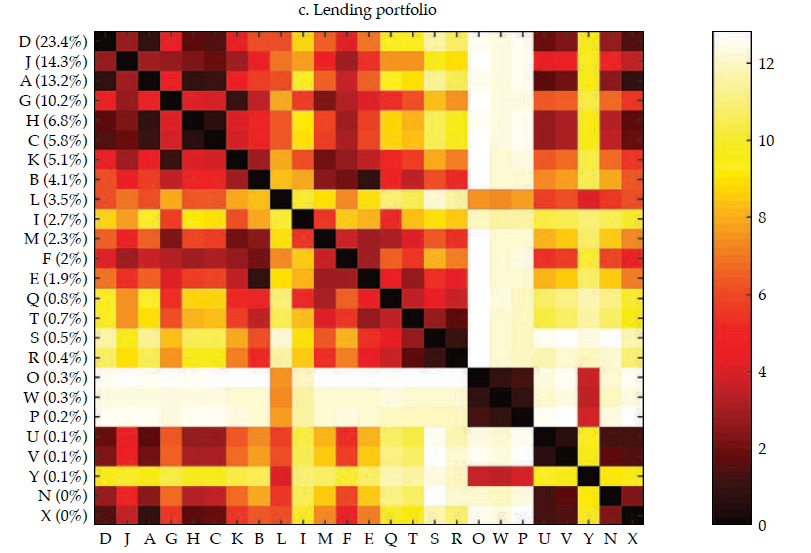
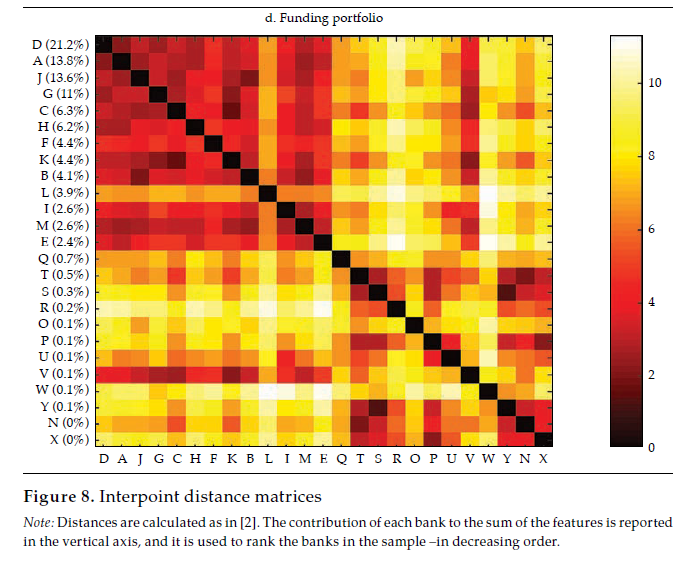
Fi gu re 3 exhibits a visualization for each bank (in rows) of each set of standardized features (in columns) that compose financial statements and the three selected portfolios (i.e., investment, lending, and funding). The contribution of each bank to the sum of the features is reported in the vertical axis and is used to rank the banks in the sample, in decreasing order. From this visualization, it is apparent that there is some degree of homogeneity in the financial structure of banks for the four sets of features. However, it is also apparent that the degree of homogeneity varies across the four sets. For instance, the funding portfolio displays a hefty similarity among banks, with a clear overlapping of funding sources in the 11-15 feature range (in the horizontal axis).
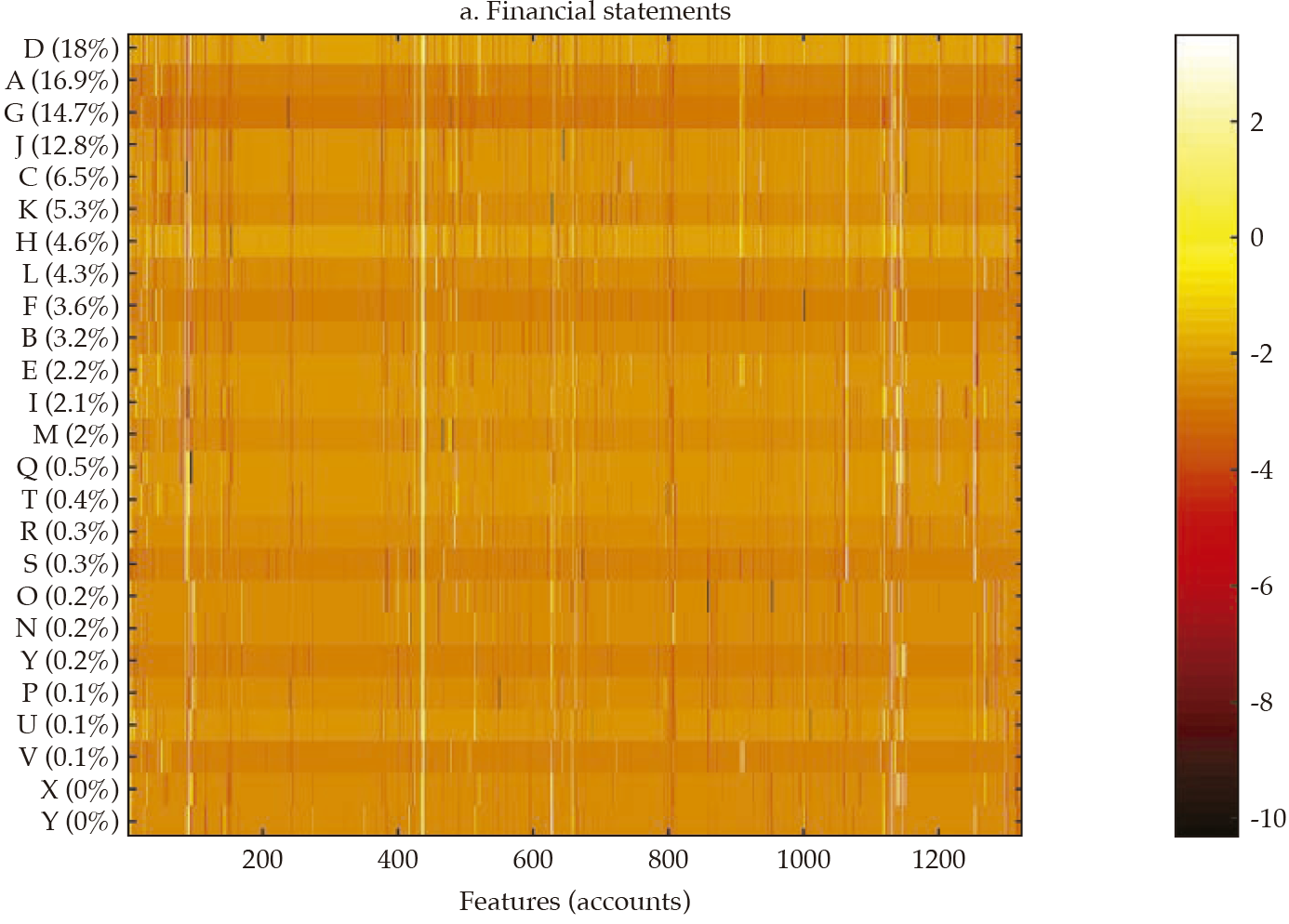
Note: Heatmap of each bank (in rows) of each set of standardized features (in columns) that compose financial statements and the three selected portfolios (i.e., investment, lending, and funding); the contribution of each bank to the sum of the features is reported in the vertical axis, and it is used to rank the banks in the sample, in decreasing order.
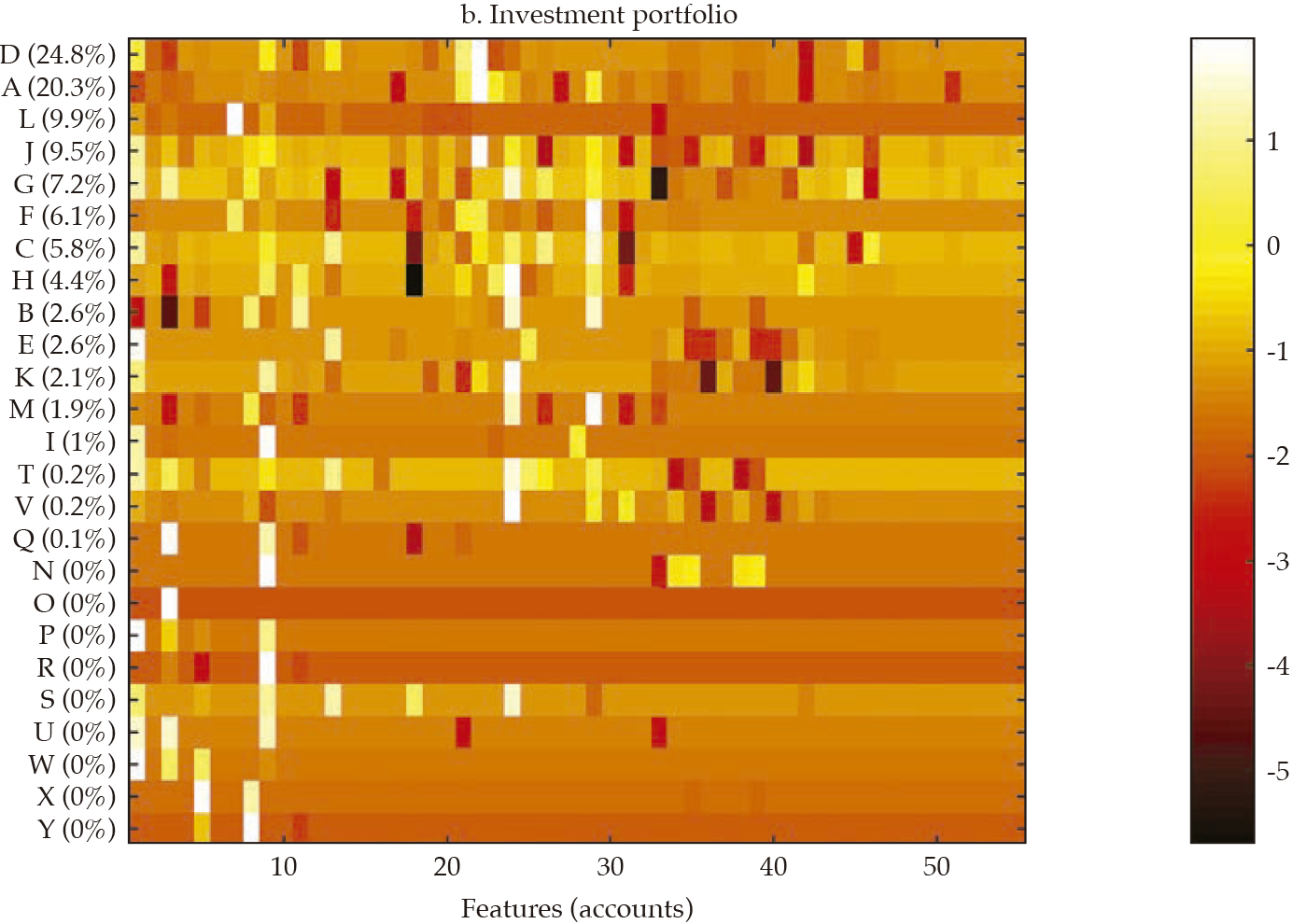
Note: Heatmap of each bank (in rows) of each set of standardized features (in columns) that compose financial statements and the three selected portfolios (i.e., investment, lending, and funding); the contribution of each bank to the sum of the features is reported in the vertical axis, and it is used to rank the banks in the sample, in decreasing order.
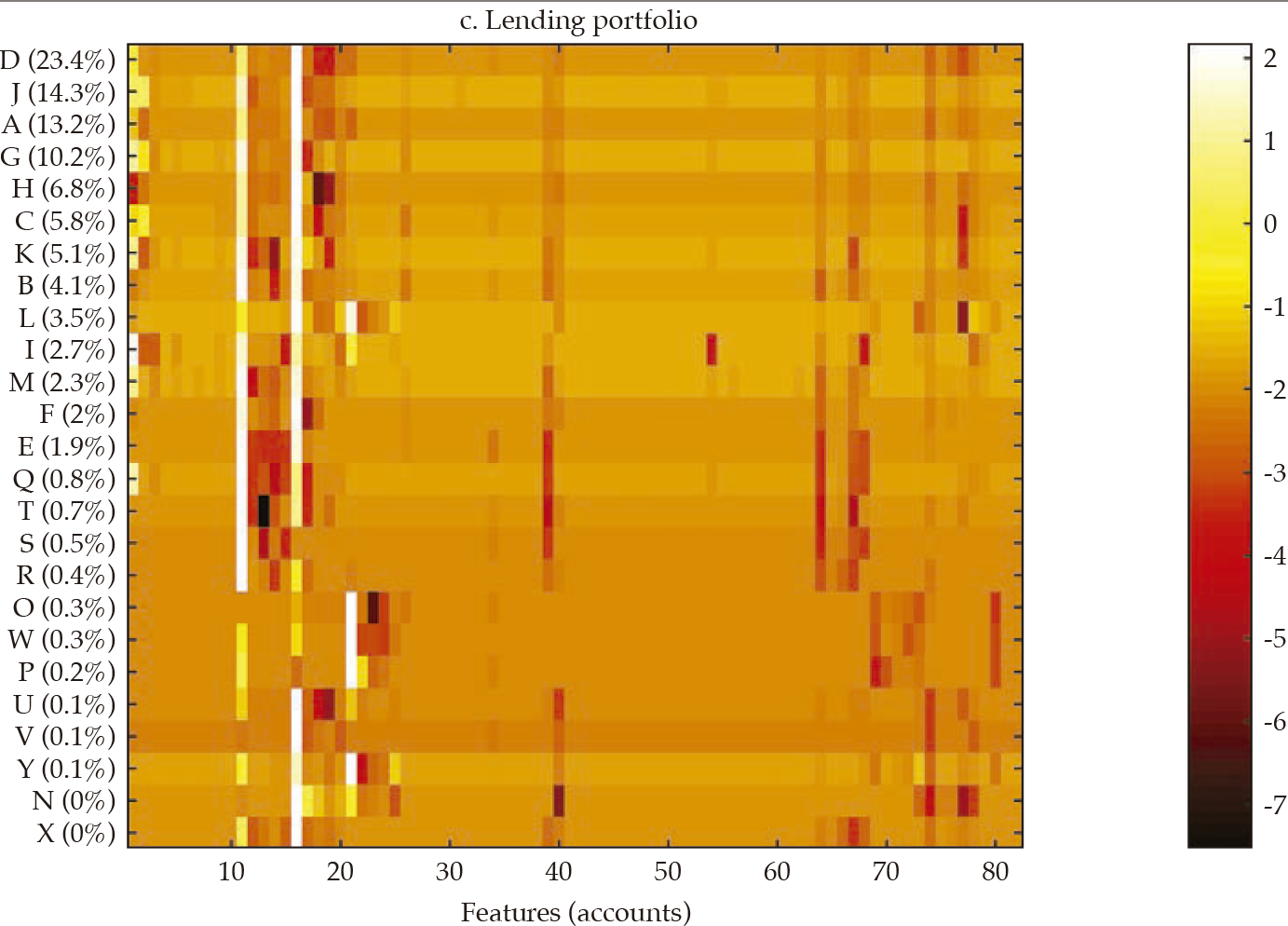
Note: Heatmap of each bank (in rows) of each set of standardized features (in columns) that compose financial statements and the three selected portfolios (i.e., investment, lending, and funding); the contribution of each bank to the sum of the features is reported in the vertical axis, and it is used to rank the banks in the sample, in decreasing order.
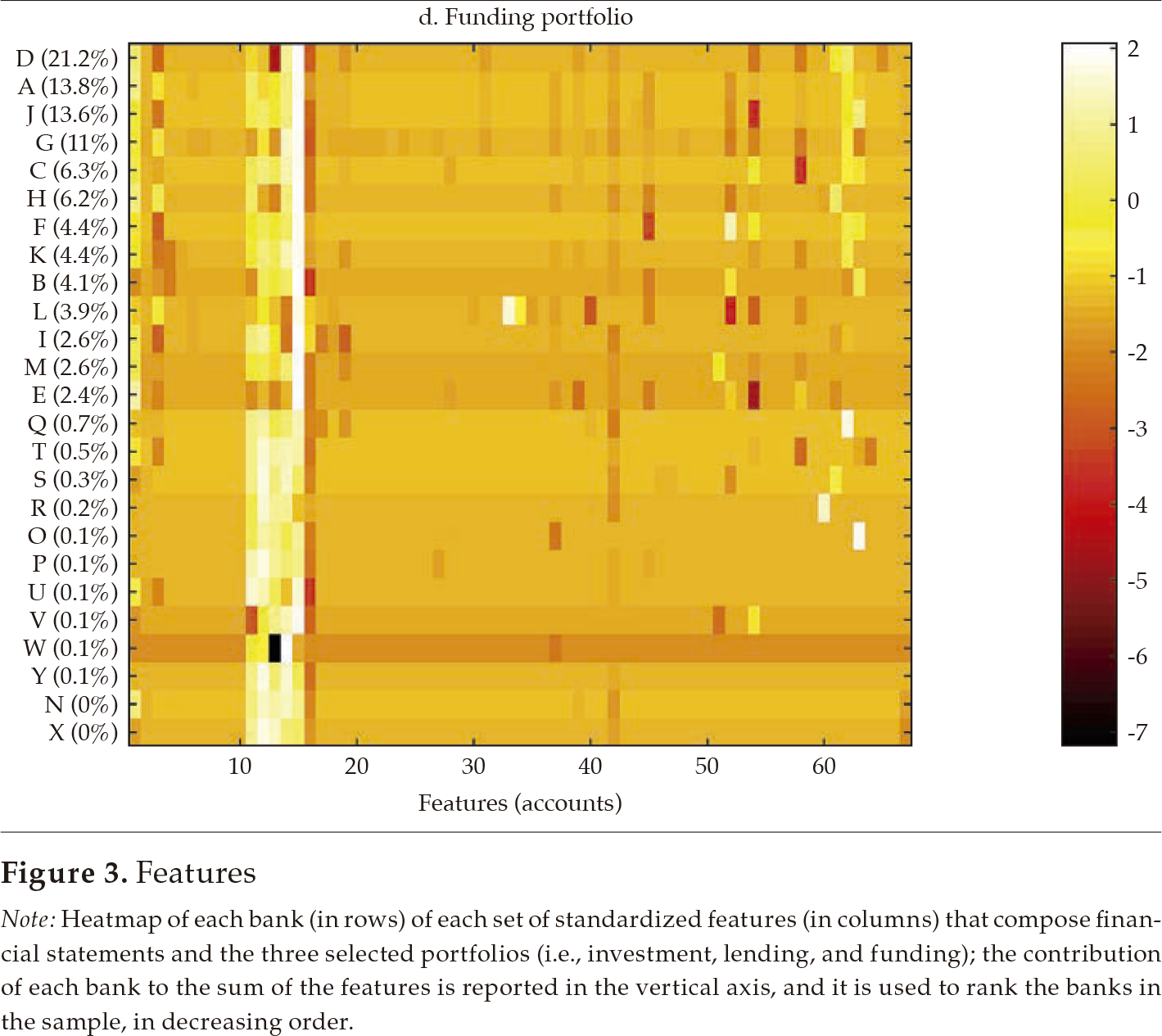
Note: Heatmap of each bank (in rows) of each set of standardized features (in columns) that compose financial statements and the three selected portfolios (i.e., investment, lending, and funding); the contribution of each bank to the sum of the features is reported in the vertical axis, and it is used to rank the banks in the sample, in decreasing order.
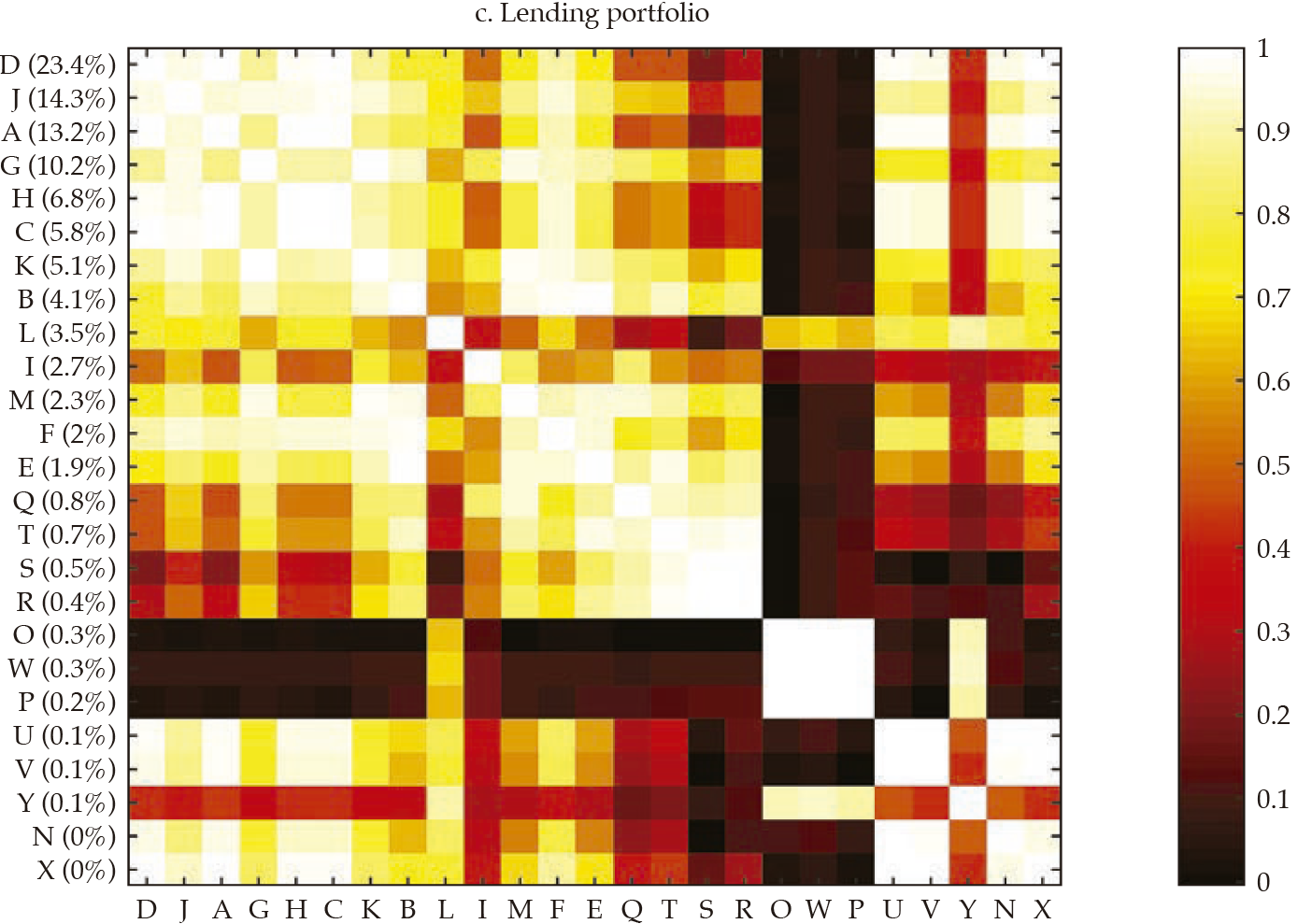
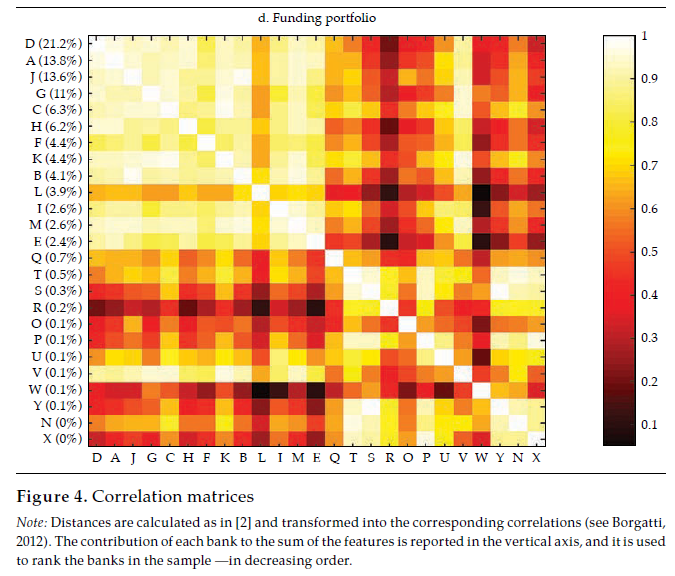
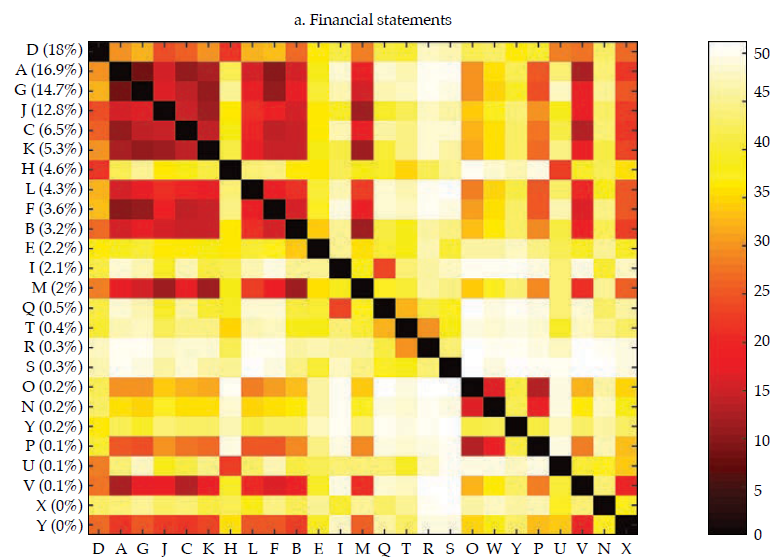
Afterward, we built the interpoint distance matrix as in [2]. By construction, the interpoint distance matrix has a lower bound (if i = j, dij= 0) but has no obvious upper bound; hence its interpretation and comparison may be burdensome. Interestingly, as stated by Borgatti (2012), if observations are standardized (i.e., as in a z-score), there is an equivalence between Euclidean distance (dij ) and correlation (rij).12 Therefore, it is easy to interpret the correlation because it is bounded to the interval [−1, 1], with −1 corresponding to the most distant and 1 to the closest, Figure 4 exhibits a visualization of the resulting correlation matrices for the entire financial statements and the three selected portfolios (i.e., investment, lending, and funding).13

Note: Distances are calculated as in [2] and transformed into the corresponding correlations (see Borgatti, 2012). The contribution of each bank to the sum of the features is reported in the vertical axis, and it is used to rank the banks in the sample —in decreasing order.
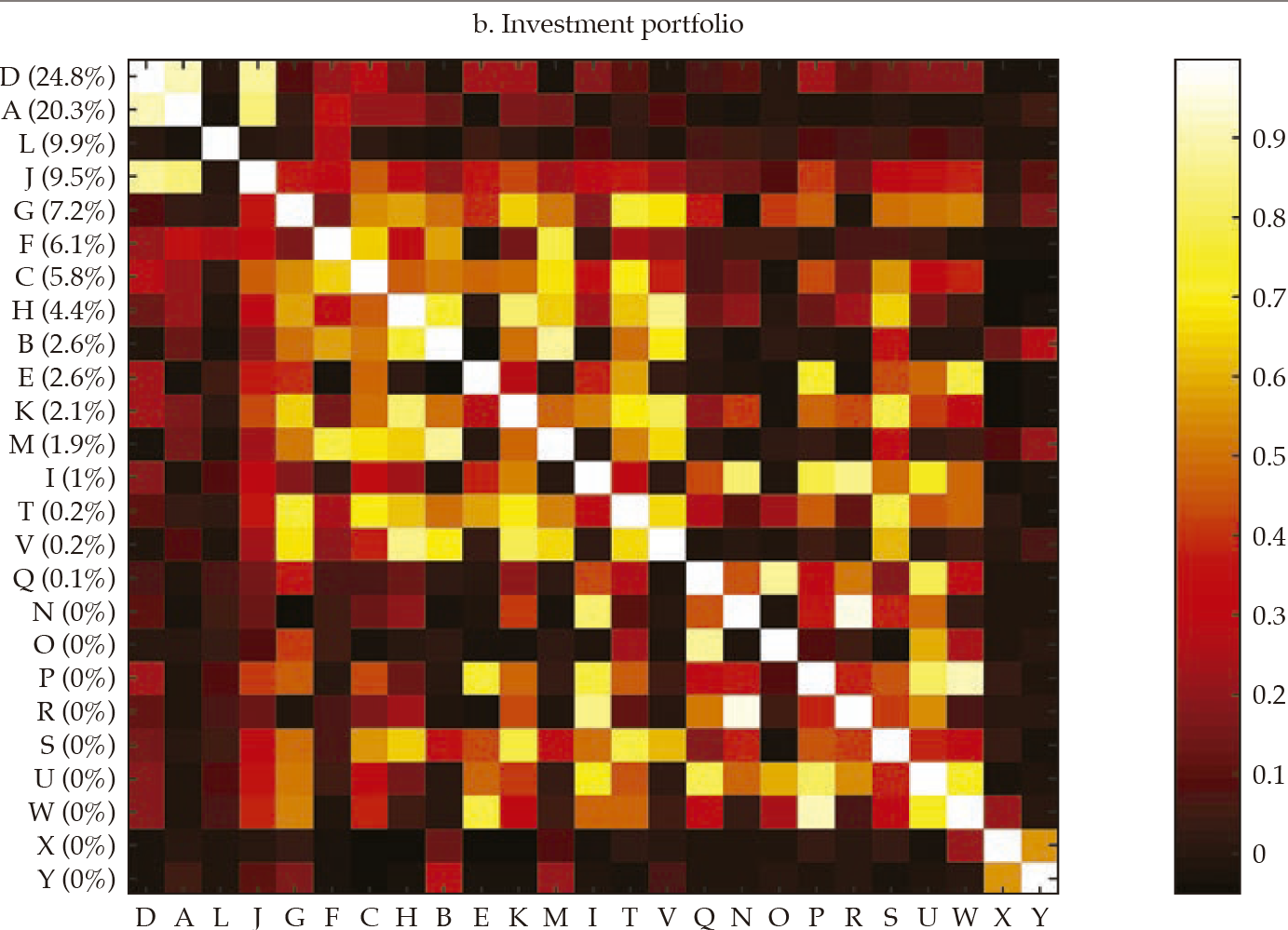
Note: Distances are calculated as in [2] and transformed into the corresponding correlations (see Borgatti, 2012). The contribution of each bank to the sum of the features is reported in the vertical axis, and it is used to rank the banks in the sample —in decreasing order.
Note: Distances are calculated as in [2] and transformed into the corresponding correlations (see Borgatti, 2012). The contribution of each bank to the sum of the features is reported in the vertical axis, and it is used to rank the banks in the sample —in decreasing order.
Note: Distances are calculated as in [2] and transformed into the corresponding correlations (see Borgatti, 2012). The contribution of each bank to the sum of the features is reported in the vertical axis, and it is used to rank the banks in the sample —in decreasing order.
Akin to figure 3, the vertical axis reports the contribution of each bank to the sum of the features, which was used to rank the banks in the sample, in decreasing order. It is rather apparent that those that contribute the most to the entire financial statements tend to display a lower distance (i.e., higher correlation); thus, they tend to be similar, which results in overlaps with Goodhart and Wagner (2012) and Fricke (2016) regarding the homogeneity of large financial institutions. It is noticeable that for the three portfolios, the top contributors are alike (banks D, A, J), and they tend to display particularly high correlations among them, which may be readily interpreted as they are holding rather similar financial statements. Regarding those that contribute the less, results are mixed; yet, there are low-contributing banks that share rather common portfolios (i.e., banks O, W, and P in the lending portfolio). All in all, from visual inspection of figure4, it is apparent that the investment portfolio is less homogeneous (i.e., less correlated), whereas the funding portfolio is the most.
Figure 5 compares the cumulative probability distribution of correlations for the four matrices in figure 4; table 1 (in Appendix) exhibits the main descriptive statistics of each distribution. It is rather obvious that the investment portfolio is the one exhibiting less correlated (i.e., more distant) banks. The investment portfolio is the only one with a non-negligible number of negative correlations, but they all are not manifestly different from zero. The funding portfolio and the lending portfolio are those in which banks tend to be more correlated. For instance, the average correlation for the funding and lending portfolio is .65 and .57, respectively, whereas for the investment portfolio is .24.
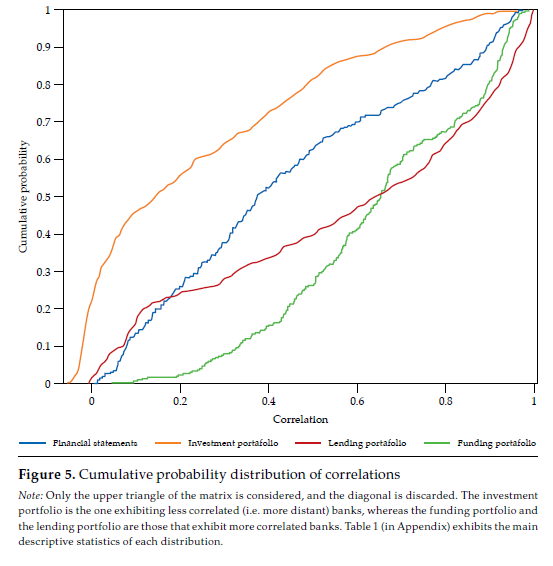
Note: Only the upper triangle of the matrix is considered, and the diagonal is discarded. The investment portfolio is the one exhibiting less correlated (i.e. more distant) banks, whereas the funding portfolio and the lending portfolio are those that exhibit more correlated banks. Table 1 (in Appendix) exhibits the main descriptive statistics of each distribution.
Main Results
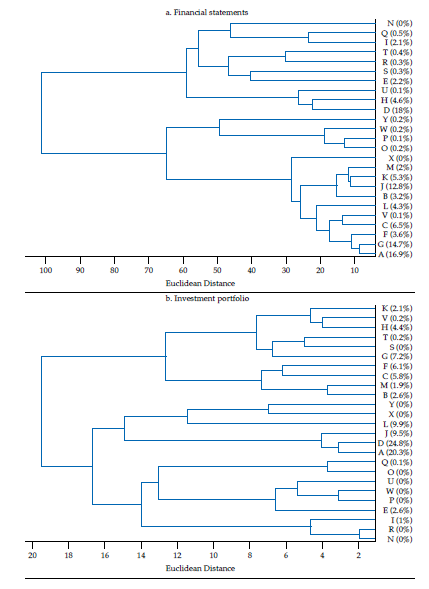
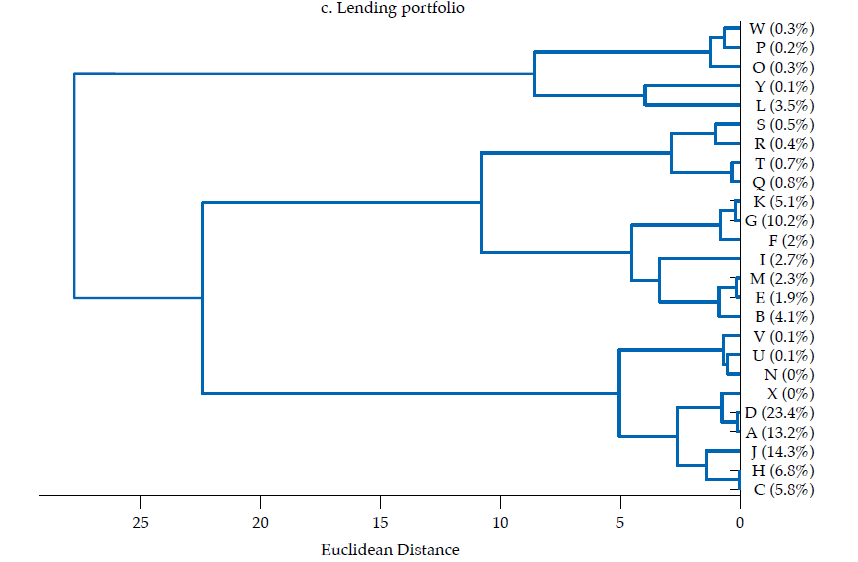
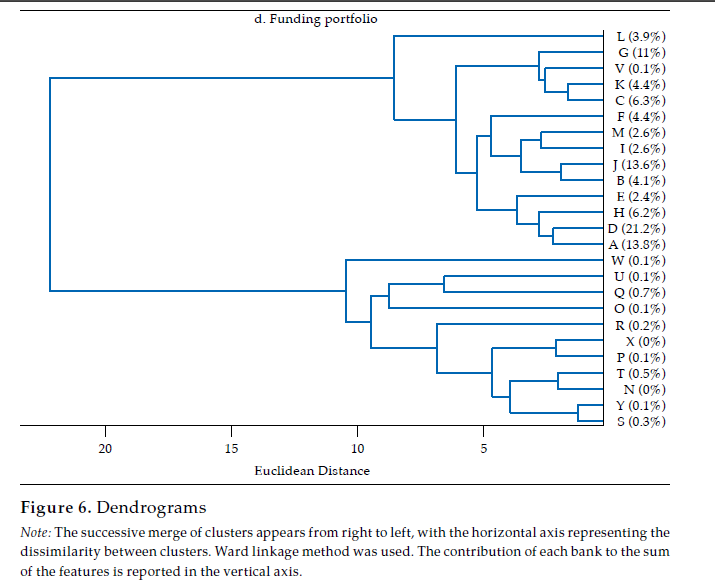
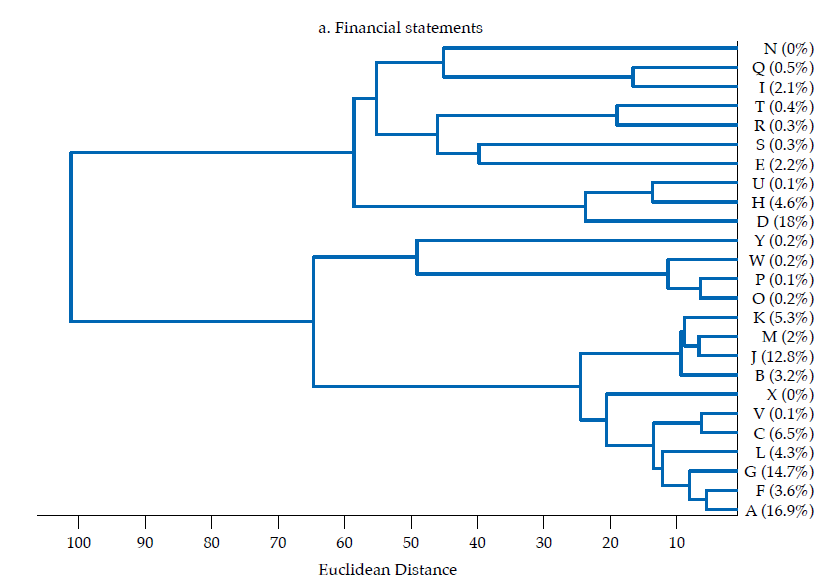
The hierarchical classifications produced by agglomerative clustering are represented by a dendrogram or tree diagram, which illustrates the successive merges made at each stage of the procedure (Everitt et al., 2011). We used horizontal dendrograms, in which the clusters’ successive merge appears from right to left, with the horizontal axis representing the dissimilarity between clusters. As exhibited in figure9 (in Appendix), the Ward linkage method dominates the Calinski and Harabasz index (i.e., validity in terms of clusters’ compactness and separateness); therefore, we present and discuss the dendrograms corresponding to Ward linkage method only.14 As correlation is easier to interpret, we discuss similarity and clusters in those terms (rij), reported in figure 4.
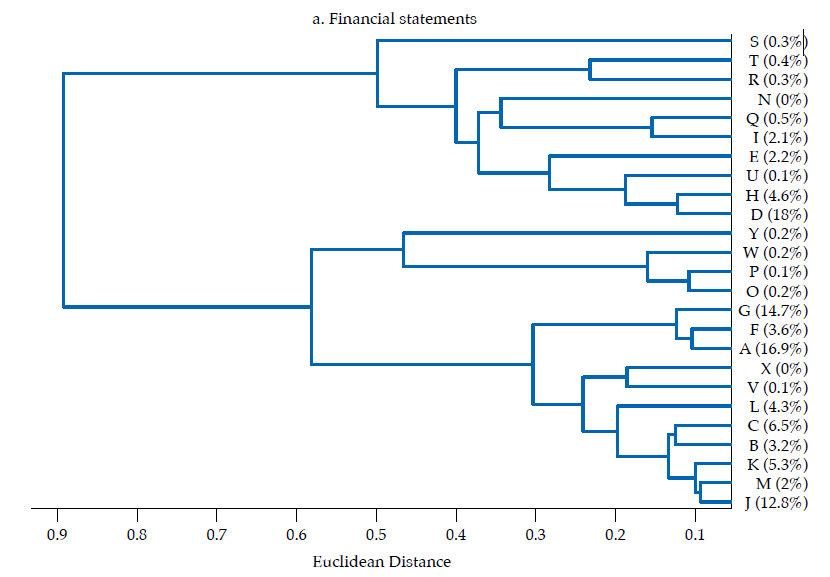
The first panel in figure 6 exhibits the dendrogram corresponding to the similarity of financial statements. Two main clusters are evident. The two most similar banks by the structure of their balance sheets are G and A (rGA= .97), which contribute to about 32 % of the sum of features (i.e., they are the second and fourth by contribution). Banks G and A are similar to bank F as well (rGF= .95; rAF= .96). The largest bank by contribution (D) does not resemble banks G, A, or F, but it is similar to bank H (rDH= .81). Consistent with figure 4, it is evident that a subset of banks tend to be rather similar: banks A, G, F, C, V, L, B, J, K, M, contributing with about 70 % of the sum of features, displays low Euclidean distances, corresponding to correlations surpassing .80. In terms of size, these ten banks account for about 63% of banking firms’ assets. Therefore, as the overall financial structure of a representative set of banks is fairly similar, it is arguable that a large part of the banking sector is exposed to similar shocks from an overall financial structure perspective. Although the largest bank by asset size (D) is not that similar to those in that ten-bank cluster, the average correlation with that set is about .68.
Note: The successive merge of clusters appears from right to left, with the horizontal axis representing the dissimilarity between clusters. Ward linkage method was used. The contribution of each bank to the sum of the features is reported in the vertical axis.
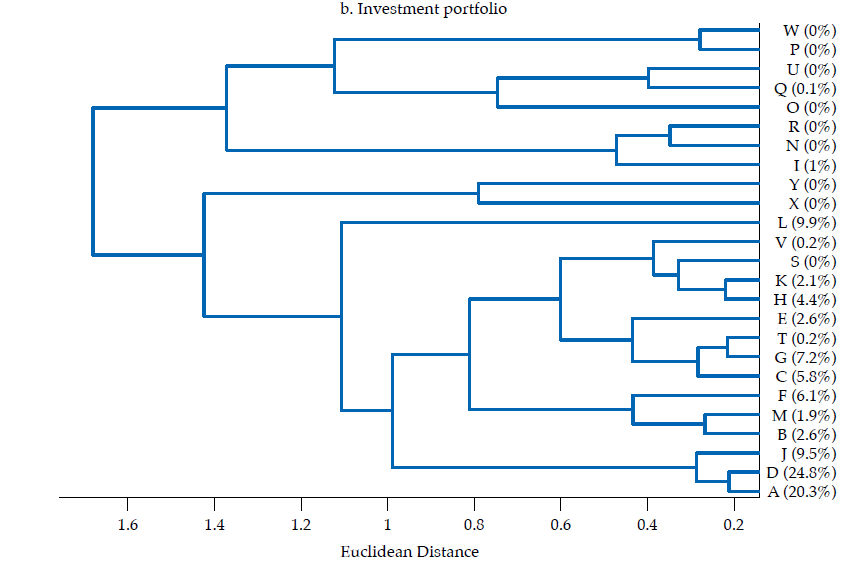
Note: The successive merge of clusters appears from right to left, with the horizontal axis representing the dissimilarity between clusters. Ward linkage method was used. The contribution of each bank to the sum of the features is reported in the vertical axis.
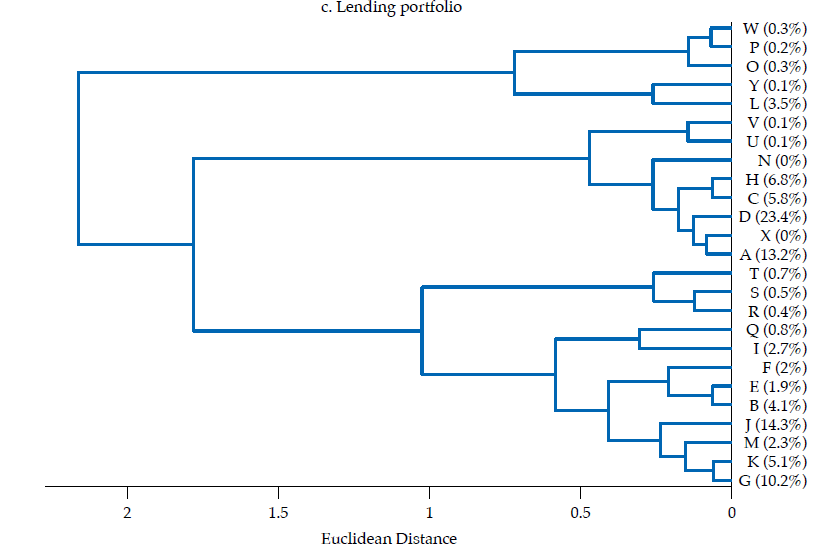
Note: The successive merge of clusters appears from right to left, with the horizontal axis representing the dissimilarity between clusters. Ward linkage method was used. The contribution of each bank to the sum of the features is reported in the vertical axis.
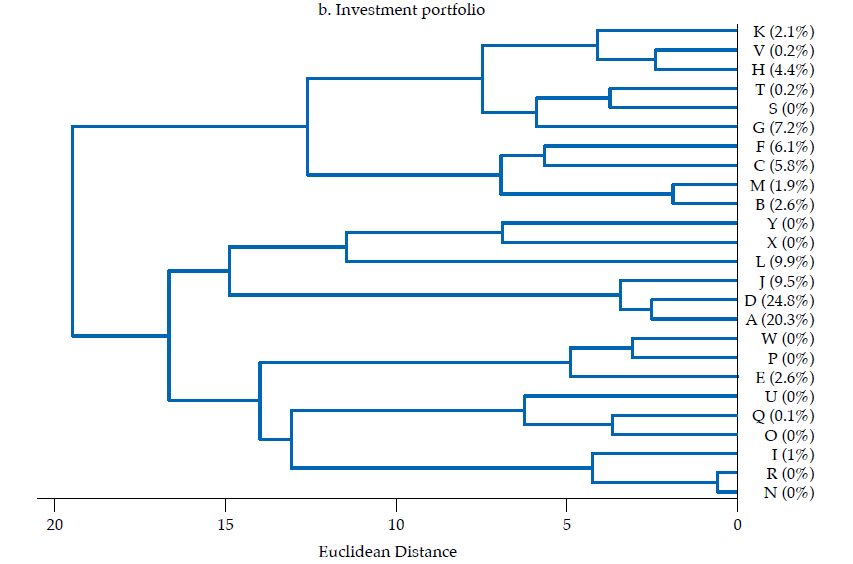
The second panel in figure 6 exhibits the dendrogram corresponding to the similarity of investment portfolios. Two main clusters are evident: one with ten banks contributing about 31 % of investment portfolios’ total value, the other with 15 banks contributing the remaining 69 %. The two most similar banks by the structure of their investment portfolios are R and N (rRN= .97), but their contribution to the sum of features (i.e., size of the investment portfolio) is nil. However, the second two most similar banks are D and A (rDA= .91), and they contribute with about 45 % to the sum of features. Bank J is also similar to D and A (rDJ= .88; rAJ= .85), with all three banks contributing with about 55 % of the sum of features. Therefore, despite most banks’ investment portfolios are not very similar (i.e., the average correlation is .24), the overlapping of three rather contributive banks (D, A, J) is noteworthy.
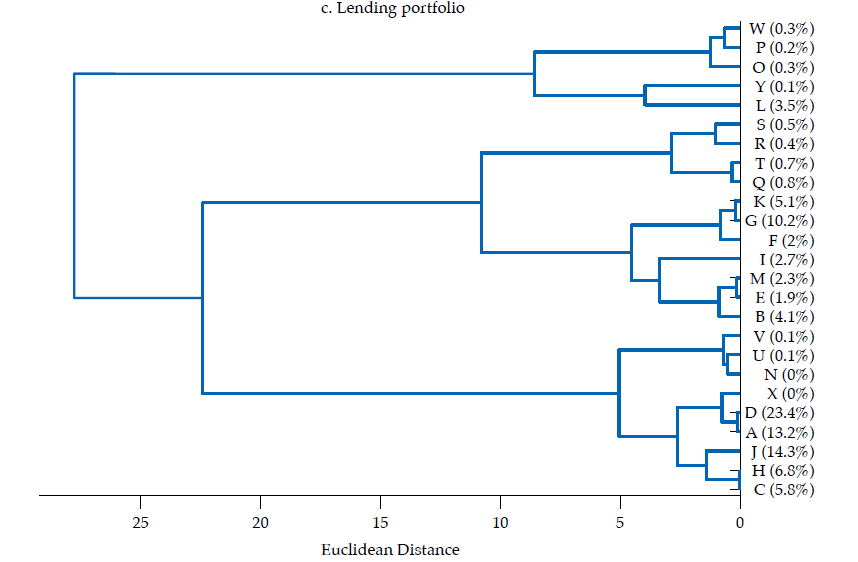
The third panel in figure6 exhibits the dendrogram corresponding to the similarity of lending portfolios. Two main clusters are evident: one with five banks contributing about 5 % of lending portfolios’ total value, the other with 20 banks, the remaining 95 %. There are several pairs of banks that share an almost identical lending portfolio structure, namely H and C, V and U, W and P, E and B, D and A, K and G, and S and R, all exhibiting correlations about .99. Although most of those pairs do not contribute manifestly to the sum of the features in the lending portfolio, the pair corresponding to D and A contribute with about 37 %, whereas K and G contribute with about 15 %. Moreover, the cluster of banks composed by C, H, A, D, X, J, N, U, V exhibits quite similar portfolios, with a mean correlation of .96, with a .86 minimum and .99 maximum. As this cluster contributes with about 64 % of the sum of features of the lending portfolio, it is fair to say that there is a significant overlap in the lending portfolio of banking firms. Also, it is fair to say that the largest banks tend to have an almost identical lending portfolio.
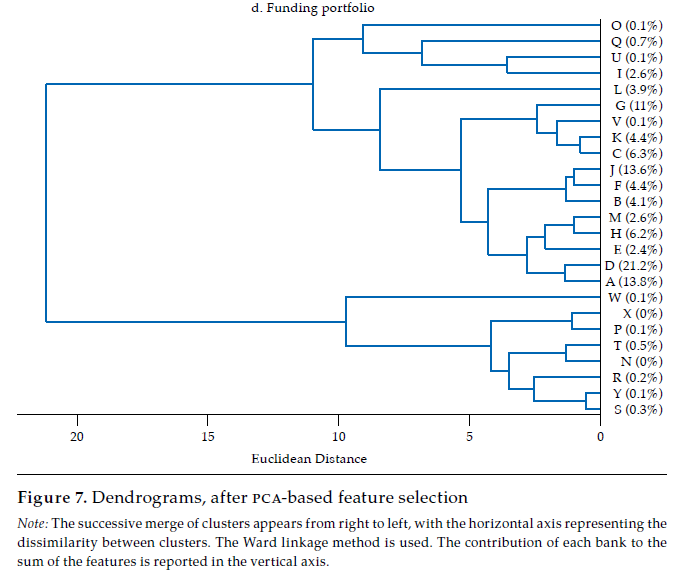
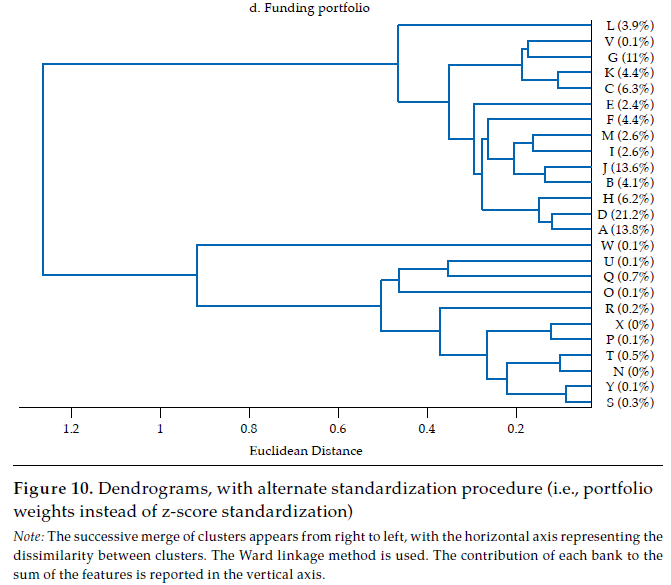
The last panel in figure 6 exhibits the dendrogram corresponding to the similarity of funding portfolios. Two main clusters are evident: one with fourteen banks contributing about 97 % of funding portfolios’ total value, the other with eleven banks, the remaining 3 percent. In the first of these clusters, there are some pairs of banks that share an almost identical funding portfolio structure, namely K and C (rKC= .98), J and B (rJB = .97), and D and A (rDA= .96). Banks in this first cluster (i.e., A, D, H, E, B, J, I, M, F, C, K, V, G, L) exhibit quite similar funding portfolios, with a mean correlation of .87, with a .62 minimum and .98 maximum. Thus, as is the case with the lending portfolio, it is fair to say that there is a significant overlap in the funding portfolio of banking firms as well.
All in all, it is rather evident that Colombian banks’ financial structure displays some degree of similarity, which reveals that they are homogeneous to some extent. The structure of financial statements and of the three portfolios (i.e., lending, investment, and funding) exhibit strong correlations that reveal how similar banks are in cross-section. Furthermore, the clusters attained by means of grouping by similarity show that banks contributing the most to financial statements or to each portfolio tend to cluster together (i.e., to be similar). This exposes that there is an important degree of homogeneity in the Colombian banking sector, in which most contributive banks share a rather common financial structure; this overlaps with findings by Fricke (2016), who reports that in the Japanese case the largest banks have become more similar over time. Under specific circumstances, such homogeneity may become problematic as it corresponds to a state of banks potentially herding together and being exposed to common shocks by the adoption of a similar set of positions. On the other hand, non-contributive banks displaying different financial structures suggest that their size may determine their ability or willingness to follow the prevalent financial structure.
Regarding how similarity diverges between financial statements and the three portfolios here considered, it is remarkable that the lending portfolio and the funding portfolio exhibit the most homogeneous structures, which suggests that the core banking function, namely, the intermediation of funds, tends to follow a common structure; yet, as the datasets are not granular enough to discriminate between the funds’ lenders and borrowers, there are numerous sources of heterogeneity to be accounted. It is also remarkable that a pair of banks, D and A, are consistently among the most similar in the investment, lending and funding portfolios; the average correlation between these two banks in the three portfolios is about .91. As D and A are the two largest banks by asset size (i.e., about 38 % of assets, 23 and 15 %, respectively), their high similarity is not to be overlooked.
Robustness Check by Feature Selection
In our case, the unique granularity of the dataset introduces the well-known dimensionality problem. For instance, when working on financial statements, we are classifying 25 banks, based on 3063 potentially redundant and noisy features. Feature selection is about finding . of . dimensions that give the most information while discarding the other (d − k) dimensions (Alpaydin, 2014). That is, feature selection enables us to construct a new set of variables that hold the latent features that contain most of the information about how banks differ in cross-section.
Principal Component Analysis (pcA) is a customary dimensionality reduction technique introduced by Pearson (1901) that is commonly used as a feature selection method. PCA aims to perform an orthogonal transformation of the data to find high-variance directions while discarding low-variance ones (Mehta et al., 2019). In this vein, PCA is an unsupervised method for feature selection, which finds a mapping from the inputs in the original .-dimensional space into a new (k < d)-dimensional space, with minimum loss of information (Alpaydin, 2014).15
Let X be a (q × d) matrix containing the original q-observation (i.e., banks) and d- dimension (i.e., features) data, and A = XTX the (d × d) covariance matrix of X, PCA is based on the eigenvector or spectral decomposition of the covariance matrix A, which states that any matrix A ∈ ℝd×d can be written as
 [3]
[3]In this setting, Λ is a diagonal (d × d) matrix in which diagonal entries correspond to the eigenvalues of A, Λ = diag(λ1, λ2, … , λd) , such that λ1 ≥ λ2 ≥ … λd, and Γ is a (d × d) matrix containing the eigenvectors as columns paired to the eigenvalues, such that the i-th column contains the i-th eigenvector. By construction, the first principal component, corresponding to the first column in Γ, lies in the direction of maximum variance of the samples, whereas the second column corresponds to the direction of maximum variance in the remaining data (except for the variance represented by the first component), and so on (Ding & Tian, 2016).
When used as a dimensionality reduction technique, the main objective of PCA is to reduce the dimensionality from d to k ≪ d while retaining most variance in the original data (i.e., without losing too much information). The fraction of variance retained when reducing the dimensionality from d to k is given by the cumulative percentage contribution of the first k-th eigenvalues to the sum of eigenvalues,
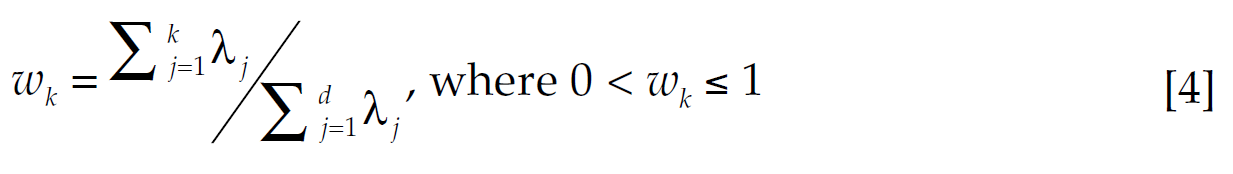 [4]
[4]Reducing dimensions from d to k yields a (d × k) matrix Γ̅ . This matrix contains the top . eigenvectors (in columns) corresponding to the first . eigenvalues from [3], with a retained variance equal to wk . From Γ̅ , a lower dimension projection of the data is attained by calculating Xˆ in [5] (see, Mehta et al., 2019). As Xˆ is a (q × k) projection matrix that retains most variance from (q × d) original matrix X, Xˆ serves as a low-dimension representation of the original dataset, suitable for feature selection purposes.
 [5]
[5]In our case, we choose a minimum retained variance target of 90 %. That is, we performed the PCA technique and chose the minimum number of . eigenvectors that correspond to that variance target. Under this choice, for the financial statements, the number of features is reduced from 3063 to 9, with wk= .95; for the investment portfolio the number of features is reduced from 55 to 10, with wk = .97; for the lending portfolio the number of features is reduced from 82 to 3, with wk= .97; and for the funding portfolio from 67 to 6 features, with wk= .96.16Figure 7 exhibits the dendrograms corresponding to the similarity of banks’ financial statements, investment portfolios, lending portfolios, and funding portfolios, based on the projection matrix that results from the feature selection procedure.
The inspection of figure7 and 6 shows that the main analytical insights remain after reducing the dimensionality of the dataset. In both figures, the homogeneity among banks contributing the most to financial statements or to each portfolio is unmistakable. Again, banks D and A, the two largest banks by size in Colombia, are among the most similar in the three portfolios. Likewise, the main hierarchical structure of the dendrograms is preserved after feature selection. Consequently, it is fair to say that results are robust to a feature selection procedure.
Note: The successive merge of clusters appears from right to left, with the horizontal axis representing the dissimilarity between clusters. The Ward linkage method is used. The contribution of each bank to the sum of the features is reported in the vertical axis.
Note: The successive merge of clusters appears from right to left, with the horizontal axis representing the dissimilarity between clusters. The Ward linkage method is used. The contribution of each bank to the sum of the features is reported in the vertical axis.
Note: The successive merge of clusters appears from right to left, with the horizontal axis representing the dissimilarity between clusters. The Ward linkage method is used. The contribution of each bank to the sum of the features is reported in the vertical axis.
Note: The successive merge of clusters appears from right to left, with the horizontal axis representing the dissimilarity between clusters. The Ward linkage method is used. The contribution of each bank to the sum of the features is reported in the vertical axis.
Final Remarks
The literature agrees on the perils arising from financial institutions’ homogeneity (see, Wagner, 2008; Haldane, 2009; Haldane & May, 2011; Beale et al., 2011; Allen et al., 2012; Goodhart & Wagner, 2012; Caccioli et al., 2014). Homogeneity, in the form of overlapping portfolios or similar financial positions, by providing a vector of contagion, has the potential of making a complex financial system vulnerable to joint failures (i.e., systemic risk) and prone to financial instability.
Accordingly, there is an ongoing discussion regarding how financial authorities should counter financial institutions’ homogeneity (i.e., encouraging diversity, increasing capital requirements, restricting activities), namely, for preserving financial stability and overall welfare (see, Wagner, 2008; Ibragimov et al, 2011; Beale et al., 2011). It appears that the aim of financial authorities’ intervention should be to weaken the connectedness of financial systems by making financial institutions less similar (i.e., more independent); this, in turn, should contribute to a lower incidence of systemic risk and financial instability. Nevertheless, due to the evidence of a non-linear and context-dependent relation between homogeneity and financial stability (see, Elliot et al., 2014; Caccioli et al., 2014; Roncoroni et al., 2019), how financial authorities should counter homogeneity is an intricate issue to be further studied. This adds to other challenges related to homogeneity, such as enhancing information, developing suitable measurements, and designing the corresponding set of policies.
Our work contributes to related literature by measuring homogeneity based on an unusually granular decomposition of Colombian banks’ financial statements. Not only empirical works that measure homogeneity are scarce, but techniques to identify groups of banks that are similar by their financial structure are absent from related literature, to the best of our knowledge. In this vein, our work presents a novel application of unsupervised machine learning techniques to the examination of otherwise unexploited large and granular financial datasets. Also, our work adds to traditional approaches that pursue cross-section examination of banks with the convenience of mitigating selection bias, by working on raw data instead of using a set of arbitrarily selected financial ratios that may discard useful information.
Results suggest that the Colombian banking sector displays some degree of homogeneity. Overall, size is a key determinant in the hierarchical structure of the banking sector. The distance among the largest banks tends to be rather low; the lending, investment, and funding portfolios of the two largest banks by asset size are particularly homogeneous. That is, akin to results reported by Fricke (2016), evidence suggests that the largest banks tend to be more similar to each other. Also, it is apparent that banks of similar size tend to cluster together. It is notable that homogeneity varies depending on the portfolio under examination: somewhat surprising, the investment portfolio is the less homogeneous, whereas the lending and funding are the most homogeneous. Results are robust to a Principal Component Analysis feature selection procedure that reduces the dimensionality of the dataset.
The empirical outcomes here reported should shed some light on the homogeneity of the Colombian banking sector. However, as homogeneity is one among many factors contributing to systemic risk, inferences are to be made with caution. The contribution of homogeneity to systemic risk and financial instability in the Colombian case is conditional on unexplored factors, such as the banking sector’s complexity and soundness, along with higher dimensions of diversity that are unavailable in financial statements. This is particularly important as, again, the relation between homogeneity and financial stability is non-linear and context-dependent (see, Elliot et al., 2014; Caccioli et al., 2014; Roncoroni et al., 2019).
Some paths of future work are worth stating. First, as datasets are available since 2015 only, a proper dynamic examination of homogeneity is pending, as in Fricke (2016). Second, as financial statements do not allow for further exploring, say, the identity, industry, or geographical location of lenders, borrowers or issuers, it is obvious that there are some other dimensions of similarity awaiting to be considered; using other types of detailed reports gathered by financial authorities or financial market infrastructures is a promising avenue of research. Third, taking into account the relevance of non-banking financial institutions (i.e., pension funds, broker-dealers), it may be convenient not to limit the examination of homogeneity to banking institutions. Fourth, as homogeneity is an additional contagion channel to counterparty and liquidity risk, aggregating them into a comprehensive measure of contagion risk is a pending challenge. Fifth, despite literature focuses on the perils arising from similarity, monitoring and examining why some banks diverge manifestly from others may be valuable for financial authorities, too. Sixth, other clustering methods may be used to contrast the empirical outcomes here reported. Finally, an explanatory model for the determinants of similarity among banks, with traditional (i.e., leverage, nonperforming loans, profitability, size, credit risk rating) and non-traditional variables (i.e., belonging to a conglomerate, relationships) is outside the scope of this article but may reveal some interesting features of the banking sector.
References
Allen, F., Babus, A., & Carletti, E. (2012). Asset commonality, debt maturity and systemic risk. Journal of Financial Economics, 104, 519-534. https://doi.org/10.1016/j.jfineco.2011.07.003
Alpaydin, E. (2014). Introduction to Machine Learning. The MIt Press: Cambridge.
Anderson, P. (1999). Complexity theory and organization science. OrganizationScience, 10(3), 216-232.
Arthur, W. B. (1999). Complexity and the economy. Science, 284, 107-109.
Aymanns, C., & Georg, C-P. (2015). Contagious synchronization and endogenous network formation in financial networks. Journal of Banking & Finance, 50, 273-285. https://doi.org/10.1016/j.jbankfin.2014.06.030
Beale, N., Rand, D., Battey, H., Croxson, K., May, R., & Nowak, M. (2011). Individual versus systemic risk and the regulator’s dilemma. Proceedings of the National Academy of Scinces of the United States of America (pnas), 108(31), 12647-12652. https://doi.org/10.1073/pnas.1105882108
Borgatti, S. (2012). Euclidean distance and correlation. Retrieved from http://www.analytictech.com/mb876/handouts/distance_and_correlation.htm
Brown, S.J., Kacperczyk, M., Ljungqvist, A., Lynch, A.W., Pedersen, L.H., & Richardson, M. (2009). Hedge funds in the aftermath of the financial crisis, In Acharya, V.V. & Richardson, M. (Eds.), Restoring financial stability. Hoboken: Wiley Finance.
Caccioli, F., Shrestha, M., Moore, C., & Farmer, J.D. (2014). Stability analysis of financial contagion due to overlapping portfolios. Journal of Banking & Finance, 46, 233-245. https://doi.org/10.1016/j.jbankfin.2014.05.021
Cai, J., Eidam, F., Saunders, A., & Steffen, S. (2017). Syndication, interconnectedness, and systemic risk. ssrn. Retrieved from: http://ssrn.com/abstract=1508642
Calinski, T., Harabasz, J. (1974). A dendrite method for cluster analysis. Communications in Statistics, 3 (1), 1-27. https://doi. org/10.1080/03610927408827101
Ding, M., & Tian, H. (2016). pcA-based network traffic anomaly detection. Tsinghua Science and Technology, 21(5), 500-509.
Elliot, M., Golub, B., & Jackson, M.O. (2014). Financial networks and contagion. The American Economic Review, 104(10), 3115-3153.
Everitt, B.S., Landau, S., Leese, M., & Stahl, D. (2011). Cluster Analysis. Chichester: Wiley.
Farmer, J.D., Gallegati, M., Hommes, C., Kirman, A., Ormerod, P., Cincotti, S., Sánchez, A., & Helbing, D. (2012). A complex systems approach to constructing better models for managing financial markets and the economy. The European Physical Journal, 214, 295-324. https://doi.org/10.1140/epjst/e2012-01696-9
Ferreira, L., & Hitchcock, D.B. (2009). A comparison of hierarchical methods for clustering functional data. Communications in Statistics – Simulation and Computation, 38 (9), 1925-1949. https://doi.org/10.1080/03610910903168603
Fricke, D. (2016). Has the banking system become more homogeneous? Evidence from banks’ loan portfolios. Economic Letters, 142, 45-48. https://doi.org/10.1016/j.econlet.2016.02.024
Gai, P., Haldane, A., & Kapadia, S. (2011). Complexity, concentration and contagion. Journal of Monetary Economics, 58, 453-470. https://doi.org/10.1016/j. jmoneco.2011.05.005
Goodhart, C. & Wagner, W. (2012). Regulators should encourage more diversity in the financial system. VoxEU. Retrieved from http://voxeu.org/article/regulators-shouldencourage-more-diversity-financial-system
Haldane, A., & May, R. (2011). Systemic risk in banking ecosystems. Nature, 469, 351-355. https://doi.org/10.1038/nature09659
Haldane, A. (June 8, 2009). Rethinking the financial network. Speech delivered at the Financial Student Association, Amsterdam.
Halkidi, M., Batistakis, Y., & Vazirgiannis, M. (2001). On clustering validation techniques. Journal of Intelligent Information Systems, 17, 107-145.
Han, J., & Kamber, M. (2006). Data mining: Concepts and techniques. San Francisco: Elsevier-Morgan Kaufman Publishers.
Hossen, B., Siraj-Ud-Doulah, & Hoque, A. (2015). Methods for evaluating agglomerative hierarchical clustering for gene expression data: a comparative study. Computational Biology and Bioinformatics, 3(6), 88-94. https://doi.org/10.11648/j.cbb.20150306.12
Huang, X., Vodenskea, I., Havlin, S., & Stanley, H.E. (2013). Cascading failures in bi-partite graphs: model for systemic risk propagation. Scientific Reports, 3, 1219. https://doi.org/10.1038/srep01219
Hüser, A-C. (2016). Too interconnected to fail: A survey of the interbank networks’ literature. safe Working Paper, 91, Goethe University Frankfurt-sAfe.
Ibragimov, R., Jaffe, D., & Walden, J. (2011). Diversification disasters. Journal of Financial Economics, 99, 333-348. https://doi.org/10.1016/j.jfineco.2010.08.015
International Monetary Fund – IMf (October, 2007). Do market risk management techniques amplify Systemic risks? Global financial stability report.
Landau, J.-P. (June 8, 2009). Complexity and the financial crisis. Introductory remarks at the Conference on The Macroeconomy and Financial Systems in Normal Times and in Times of Stress, Banque de France and Bundesbank.
León, C., Kim, G.-Y., Martínez, C., & Lee, D. (2017). Equity markets’ clustering and the global financial crisis. Quantitative Finance, 17(12), 1905-1922.
León, C., Machado, C., Cepeda, F., & Sarmiento, M. (2012). Systemic risk in large-value payment systems in Colombia: a network topology and payments simulation approach. In M. Hellqvist, & T. Laine (Eds.), Diagnostics for the financial markets – computational studies of payment system, E:45. Helsinki: Bank of Finland.
Lo, A.W. (2011). Complexity, concentration and contagion: A comment. Journal of Monetary Economics, 58, 471-479. https://doi.org/10.1016/j.jmoneco.2011.06.001
Martínez, W. L., & Martínez, A.R. (2008). Computational Statistics Handbook with Matlab. Boca Ratón: Chapman & Hall/crc.
Martínez, W.L., Martínez, A.R., & Solka, J.L. (2011). Exploratory Data Analysis with Matlab. Boca Ratón: Chapman & Hall/crc.
May, R. & Arinaminpathy, N. (2010). Systemic risk: the dynamics of model banking systems. The Journal of the Royal Society. 7, 823-838. https://doi.org/10.1098/rsif.2009.0359
May, R., Levin, S., & Sugihara, G. (2008). Ecology for bankers. Nature, 451, 893-895.
Mehta, P., Bukov, M., Wang, C-H., Day, A.G.R., Richardson, C., Fisher, C.K., & Schwab, D.J. (2019). A high-bias, low-variance introduction to machine learning for physicists. Physics Reports, 810, 1-124.
Miller, J. H., & Page, S. E. (2007). Complex adaptive systems. Princeton: Princeton University Press.
Milligan, G. W., & Cooper, M. C. (1987). Methodology review: Clustering methods. Applied Psychological Measurement, 11(4), 329-354. https://doi. org/10.1177/014662168701100401
Mitchell, M. (2011). Complexity: A guided tour. New York: Oxford University Press.
Pearson, K. (1901). On lines and planes of closest fit to systems of points in space. Philosophical Magazine, 2, 559-572.
Pool, V.K., Stoffman, N., & Yonker, S.E. (2015). The people in your neighborhood: social intercations and mutual fund portfolios. The Journal of Finance, 70(6), 2679-2731. https://doi.org/10.1111/jofi.12208
Rebonato, R. (2007). Plight of the fortune tellers. Princeton: Princeton University Press.
Roncoroni, A., Battiston, S., D’Errico, M., Halaj, G., & Kok, C. (2019). Interconnected banks and systemically important exposures. Bank of Canada Staff Working Paper, 2019-44.
Simon, H. (1962). The architecture of complexity. Proceedings of the American Philosophical Society, 106(6), 467-482.
Sornette, D. (2003). Why stock markets crash. Princeton: Princeton University Press.
Strogatz, S. (2003). sync: How order emerges from chaos in the universe, nature and daily life. New York: Hyperion Books.
Sumathi, S., & Sivanandam, S.N. (2006). Introduction to data mining and its applications. Berlin Heidelberg: Springer.
Wagner, W. (2008). The homogenization of the financial system and financial crises. Journal of Financial Intermediation, 17, 330-356. https://doi.org/10.1016/j.jfi.2008.01.001
Wagner, W. (2010). Diversification at financial institutions and systemic crises. Journal of Financial Intermediation, 19, 373-386. Doi: 10.1016/j.jfi.2009.07.002
Ward, J. H. (1963). Hierarchical grouping to optimize an objective function. Journal of the American Statistical Association, 58(301), 236-244.
Witten, I. H., Frank, E., & Hall M. A. (2011). Data mining: Practical machine learning tools and techniques. Burlington: Morgan Kaufmann.
Zhao, Z., Zhang, W., & Shi, S. (2013) Common asset holdings and systemic risk of financial network. Procedia Computer Science, 17, 1010-1014. https://doi.org/10.1016/j.procs.2013.05.128
Apendix
Note: Distances are calculated as in [2]. The contribution of each bank to the sum of the features is reported in the vertical axis, and it is used to rank the banks in the sample –in decreasing order.
Note: Distances are calculated as in [2]. The contribution of each bank to the sum of the features is reported in the vertical axis, and it is used to rank the banks in the sample –in decreasing order.
Note: Distances are calculated as in [2]. The contribution of each bank to the sum of the features is reported in the vertical axis, and it is used to rank the banks in the sample –in decreasing order.
Note: Distances are calculated as in [2]. The contribution of each bank to the sum of the features is reported in the vertical axis, and it is used to rank the banks in the sample –in decreasing order.
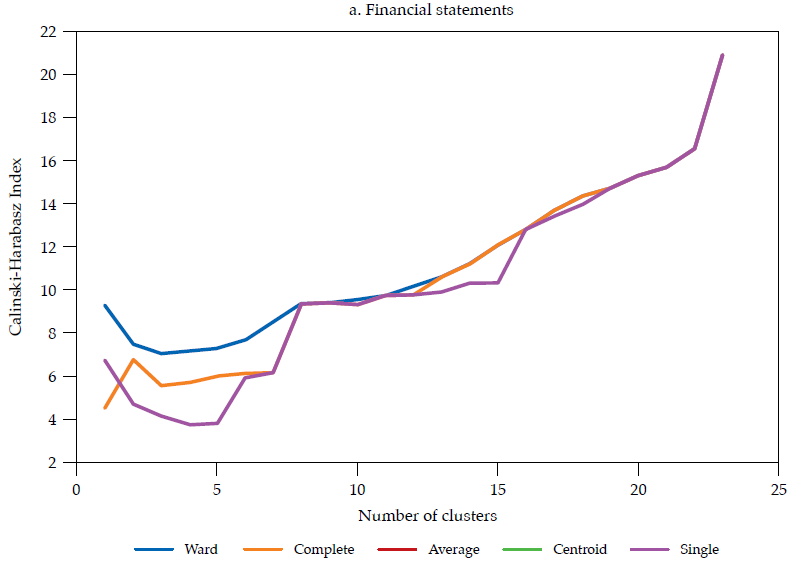
Note: Calculated as the ratio of the betweencluster distance sum of squares (i.e., separateness) to the withincluster distance sum of squares (i.e., compactness); the larger the index the better the clustering solution. Source: (Calinski & Harabasz, 1974)
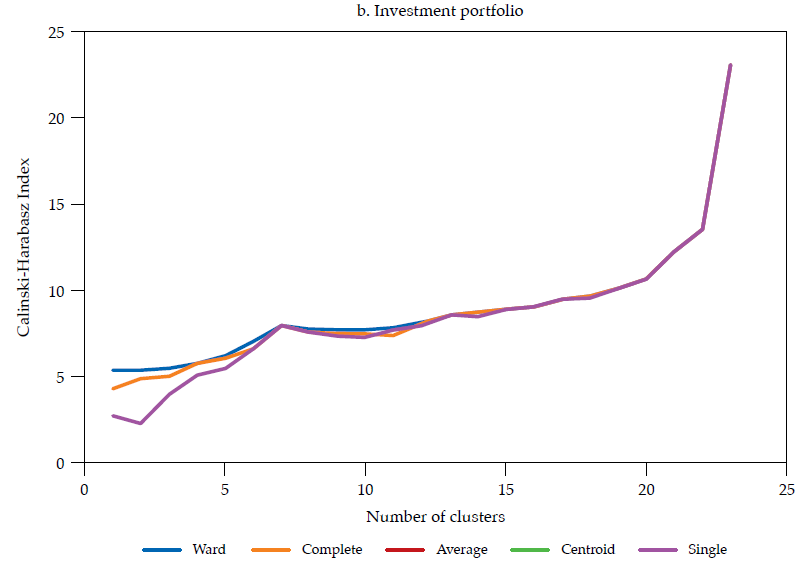
Note: Calculated as the ratio of the betweencluster distance sum of squares (i.e., separateness) to the withincluster distance sum of squares (i.e., compactness); the larger the index the better the clustering solution. Source: (Calinski & Harabasz, 1974)
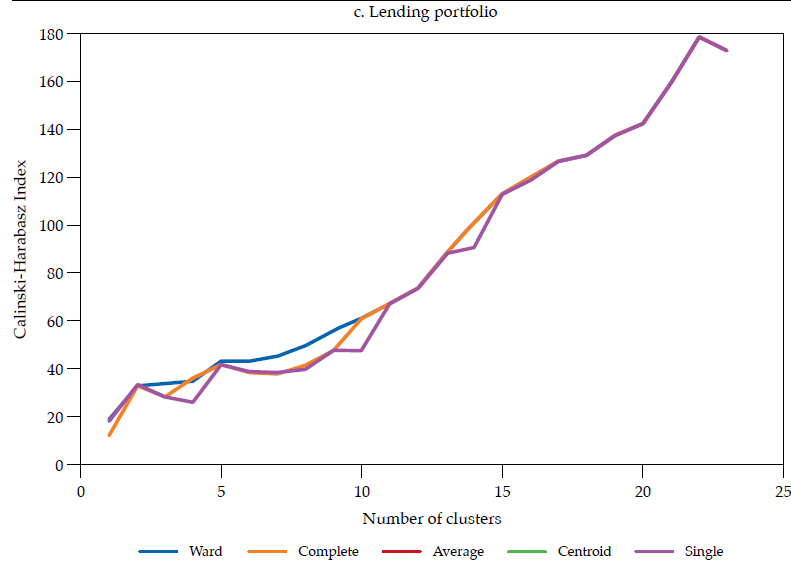
Note: Calculated as the ratio of the betweencluster distance sum of squares (i.e., separateness) to the withincluster distance sum of squares (i.e., compactness); the larger the index the better the clustering solution. Source: (Calinski & Harabasz, 1974)
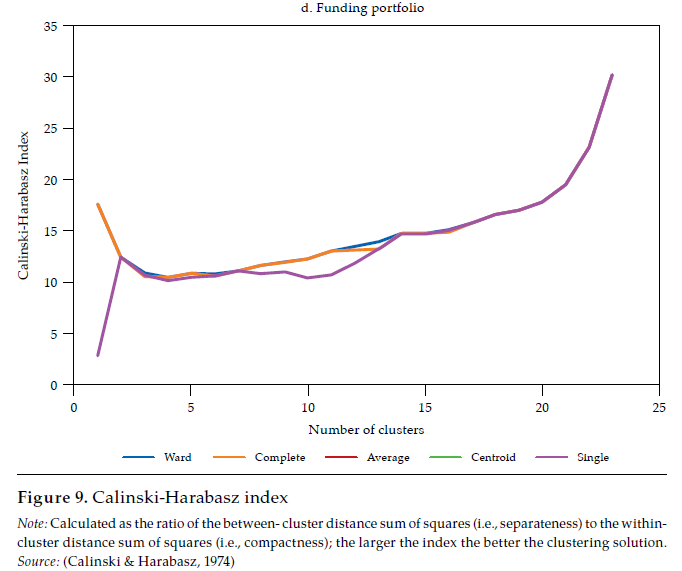
Note: Calculated as the ratio of the betweencluster distance sum of squares (i.e., separateness) to the withincluster distance sum of squares (i.e., compactness); the larger the index the better the clustering solution. Source: (Calinski & Harabasz, 1974)
Note: The successive merge of clusters appears from right to left, with the horizontal axis representing the dissimilarity between clusters. The Ward linkage method is used. The contribution of each bank to the sum of the features is reported in the vertical axis.
Note: The successive merge of clusters appears from right to left, with the horizontal axis representing the dissimilarity between clusters. The Ward linkage method is used. The contribution of each bank to the sum of the features is reported in the vertical axis.
Note: The successive merge of clusters appears from right to left, with the horizontal axis representing the dissimilarity between clusters. The Ward linkage method is used. The contribution of each bank to the sum of the features is reported in the vertical axis.
Note: The successive merge of clusters appears from right to left, with the horizontal axis representing the dissimilarity between clusters. The Ward linkage method is used. The contribution of each bank to the sum of the features is reported in the vertical axis.
Notes
1 Our definition of systemic risk follows that of several authors (i.e., Ibragimov et al., 2011; Allen et al., 2012), meaning the negative externalities of joint failures of financial institutions as a result of a common shock or a contagion process.
2 Datasets are available since 2015 (after the adoption of International Financial Reporting Standards). Thus, examining the dynamics of homogeneity for a small number of months is —in our view— inadequate at the moment.
3 Yet, there are many definitions and measures of complexity, intended for different purposes. The interested reader is referred to consult Anderson (1999) and Mitchell (2011).
4 The assumption of no links among banks and among assets may be relaxed as well. This may be convenient as banks are linked to each other because of interbank lending and asset price dynamics tend to display dependence (i.e., correlation). None of these intra-group effects are considered here but are crucial for a comprehensive portrait of risk propagation.
5 As small shocks tend to be common but mild, whereas large tend to be rare but catastrophic, the findings of Caccioli et al. (2014) and Roncoroni et al. (2019) concur with the “robust-yet-fragile” behavior of financial networks (see Haldane, 2009; Hüser, 2016). Furthermore, this concurs with complex adaptive systems literature, which points out that systems’ connective structure grants everyday stability and efficiency, but exposes them to rare massive transformations (see Miller & Page, 2007).
6 This section is based on León et al. (2017).
7 Agglomerative clustering belongs to hierarchical clustering methods —along with the less common divisive clustering method—. Other clustering methods are available such as partitioning (i.e., .-means), densitybased, spectral, and model-based (see, Han & Kamber, 2006; Martínez et al., 2011; Everitt et al., 2011). Hierarchical methods are preferred for this case as they form the backbone of cluster analysis in practice (Everitt et al., 2011), they are one of the most common approaches to clustering (Martínez et al., 2011), easy to implement as they are based on distances that may be transformed into correlations and to interpret; further, they enable displaying the entire hierarchy (i.e., the dendrogram) for analytical purposes and do not require an arbitrary selection of the number of clusters (as in .-means).
8 Euclidean distance is the most often used for continuous data because of its simplicity and interpretability as a physical distance. Other measures of distance exist as well (see, Martínez & Martínez, 2008; Everitt et al. 2011). Cai et al. (2017) chose Euclidean distance to measure the similarity between banks’ syndicated loan portfolios in the United States. When examining the homogeneity in Japanese banks’ loan portfolios, Fricke (2016) used several measures of distance, including the Euclidean distance; all measures reported to be strongly correlated, and results, robust to the choice of measure.
9 For a comprehensive explanation of the different linkage methods, their shortcomings and advantages see Everitt et al. (2011) and Martínez et al. (2011).
10 Before transforming the features, we removed those in which all banks reported figures equal to zero; this has no impact on the results (i.e., all banking firms are strictly equal with respect to those features) but may reduce computational burden and allow for clearer visualization. After removing those blank features, their number decreased from 3063 to 1327 in financial statements from 145 to 55 in the investment portfolio, from 111 to 82 in the lending portfolio, and from 139 to 67 in the funding portfolio.
11 An alternative to the chosen z-score standardization procedure is to calculate the contribution of each account to the sum of all accounts, as weights in a portfolio. However, this would make the transformation of distances into correlations (see Borgatti, 2012) impossible. As displayed in Fi gu re 10 (in Appendix), interpretation of attained hierarchical classification in the dendrograms is robust to changing the standardization procedure.
12 As in Borgatti (2012), the Euclidean distance is a sum of squared differences, whereas correlation is an average product. If series are standardized as in a z-score (i.e., mean is zero, the standard deviation is one), the correlation between two variables can be written in terms of the distance between them: rij = 1 − (dij )2 ⁄2n. As the correlation is easily interpreted and compared, this standardization method is preferred to other alternatives.
13 The inter-point distance matrices are displayed in fi gu re 8 (Appendix). As expected, they conform to an inverse mapping of the correlation matrices in figure 4.
14 Several unrelated empirical studies tend to favor Ward’s linkage method (see, Milligan & Cooper, 1987; Ferreira & Hitchcock, 2009; Everitt et al., 2011; Hossen et al., 2015).
15 A natural alternative to pcA-based feature selection is to arbitrarily select a set of features or financial ratios (from features), say earnings, return on assets, non-performing loans, leverage, etc. Nevertheless, this would entail the existence of causal theoretical models regarding the relevance of the arbitrarily selected set of features to capture crosssectional differences among banks. In our case, to avoid any sort of selection bias arising from such arbitrary selection of features, we preferred to maximize the informational content of data by employing a pcA-based feature selection method.
16 In all cases, for the minimum retained variance target of 90 %, the ratio of projection to original dimensions (k ⁄d) is low, with a maximum of about 18 % for the investment portfolio case, which points out that the feature selection procedure is able to avoid the dimensionality problem while retaining most of the data variance. This also suggests that, as expected, the data is not random.
* The opinions and statements in this article are the sole responsibility of the author and neither represent those of Banco de la República nor of its Board of Directors. Results alone may not be interpreted as conclusive or comprehensive about the systemic risk or financial stability. Any remaining errors are the author’s own. I am grateful to Jorge Cely for his work on data extraction and processing, and to Pamela Cardozo, Freddy Cepeda, Clara Machado, Hernando Vargas, and the Financial Stability Department staff for their comments. I am particularly grateful to an anonymous reviewer for his comments and suggestions.