

Pronóstico del precio de la energía en Colombia utilizando modelos ARIMA con IGARCH
Forecast of Energy Prices in Colombia Using ARIMA-IGARCH Models
Prognóstico do preço da energia na Colômbia utilizando modelos ARIMA com IGARCH
Pronóstico del precio de la energía en Colombia utilizando modelos ARIMA con IGARCH
Revista de Economía del Rosario, vol. 20, núm. 1, 2017
Universidad del Rosario
Recibido: 31 Octubre 2016
Aceptado: Junio 12, 2017
Información adicional
Para
citar este artículo: Muñoz-Santiago, A., Urquijo-Vanstrahlengs,
J., Castro-Otero, A., & Lombana, J. (2017).
Pronóstico del precio de la energía en Colombia utilizando modelos ARIMA con IGARCH. Revista de Economía del Rosario, 20(1),
127-161. Doi: https://doi.org/10.12804/revistas.urosario.edu.co/economia/a.6152
Resumen:
El precio de la energía en bolsa es uno de los commodities con más volatilidad en mercados mundiales, lo que convierte su estimación en un reto, debido a los diferentes factores intervinientes: composición del parque generador, clima, precios del petróleo, correlación entre demanda de energía y el PIB, entre otros, lo que provoca una volatilidad del precio en bolsa. El objetivo de este artículo es mostrar el modelo ARIMA con IGARCH que mejor pronostique el precio de la energía en Colombia. Se concluye que si las variables estudiadas presentan estas características: comportamientos bruscos en periodos cortos, asimetría en distribución y no cumple con supuestos de estacionariedad, es preferible aplicar los modelos ARCH, GARCH y sus diferentes derivaciones por cubrir mejor la heterocedasticidad.
Clasificación JEL: C22, Q41
Palabras clave: ARIMA, ARCH, GARCH, IGARCH, precios de la energía en bolsa.
Abstract:
The price of energy in the stock market is one of the most volatile commodities in world markets, making its estimate a challenge for the different factors involved: composition of the generating capacity, climate, oil prices, correlation between energy demand and GDP, among others, provoking price volatility in the stock market. The objective is to show the ARIMA model with IGARCH that better predicts the price of energy in Colombia. It is concluded that if the studied variables have characteristics such as: abrupt behavior in short periods of time, asymmetry in distribution and does not meet with assumptions of stationarity, it is preferable to apply ARCH, GARCH and its different derivations to better cover heteroskedasticity.
JEL Classification: C22, Q41
Keywords: ARIMA, ARCH, GARCH, IGARCH, energy stock market prices, Colombia.
Resumo:
O preço da energia em bolsa é um dos commodities com mais volatilidade em mercados mundiais, convertendo a sua estimação em um desafio pelos diferentes fatores intervenientes: composição do parque gerador, clima, preços do petróleo, correlação entre demanda de energia e PIB, entre outros, provocando volatilidade do preço em bolsa. O objetivo é mostrar o modelo ARIMA com IGARCH que melhor prognostique o preço da energia na Colômbia. Conclui-se que se as variáveis estudadas apresentam características: comportamentos bruscos em períodos curtos, assimetria em distribuição e não cumpre com supostos de estacionariedade, é preferível aplicar os modelos ARCH, GARCH e suas diferentes derivações por cobrir melhor a heterocedasticidade.
Classificação JEL: C22, Q41
Palavras-chave: ARIMA, ARCH, GARCH, IGARCH, preços da energia em bolsa.
Introducción
La predicción del precio en bolsa de energía en Colombia es un proceso que en sí mismo se convierte en un verdadero reto por los diferentes factores que intervienen en su formación, la composición del parque generador hidráulico y térmico (relación de 70:30), los eventos climáticos que tienen ocurrencias irregulares entre 2 y 7 años como El Niño (sequía) o La Niña (lluvias intensas), los precios internacionales del petróleo, la alta correlación entre la demanda de energía y el PIB (figura 1a) provocan que el precio de bolsa presente alta volatilidad (figura 1b).
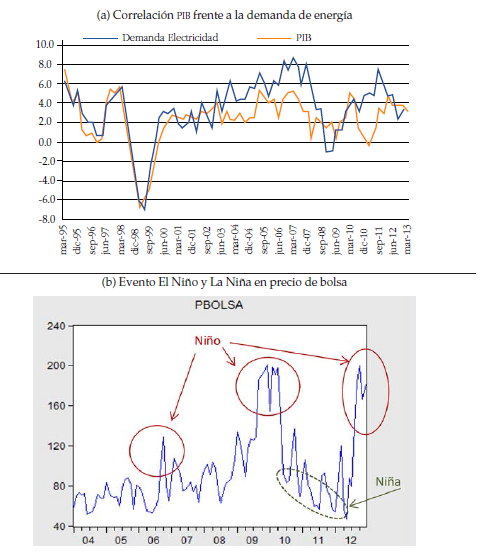
El objetivo central de este artículo es encontrar el modelo que mejor pronostique el precio de la energía en Colombia, utilizando modelos autoregresivos.
El precio de la energía eléctrica es uno de los commodities con más volatilidad en los mercados mundiales. El cambio diario o mensual del precio spot de energía puede ser de hasta el 50 %, mientras que, al mismo tiempo, para otras materias primas es de solo el 5 %. La planeación de los ingresos para los agentes o actores del sector eléctrico en Colombia, tales como generadores, comercializadores, grandes usuarios o clientes finales (grandes industriales), dependen en gran medida de la evolución del precio spot de la energía. De acá surge la importancia para estos agentes económicos de prever o desarrollar modelos de pronósticos de precios de la energía en el corto y mediano plazo.
Los Modelos Autorregresivos Integrados de Media Móvil (ARIMA) han sido utilizados en el pronóstico de precios de energía como lo muestra la publicación del Electricity Price Forecasting - ARIMA Model Approach presentado en 2011 en la conferencia Internacional del Mercado Europeo de Energía en Zagreb, Croacia (Jakaša et al. 2011). Esta publicación utiliza la serie del precio spot de energía diario en Alemania para los años 2000 a 2011. La configuración de datos se dividió en dos series. La primera de ellas corresponde a los días hábiles y la segunda a los días feriados. El modelo encontrado arroja un error cuadrático medio de 3,55 %, y como mejora al modelo sugieren considerar el efecto calendario.
Otros estudios realizados sobre la volatilidad de los precios de energía eléctrica como los de García et al. (2005), Contreras et al. (2003), Lucia y Schwartz (2002), Benini et al. (2002) y Pilipovic (1997) mencionan, entre otras recomendaciones, que la inclusión de efectos calendario, variables exógenas como la demanda, hábitos de la población, el clima y la alta dependencia de las condiciones temporales de oferta, debido a la imposibilidad de almacenamiento y a las restricciones de transporte, afectan el precio spot de la energía eléctrica.
Varios autores han propuesto diferentes modelos de pronóstico del precio de la electricidad en el corto plazo (el día siguiente). Nogales et al. (2002) y Contreras et al. (2003) utilizan, respectivamente, modelos de series de tiempo y modelos autorregresivos e integrados de promedios móviles (ARIMA) para pronosticar el precio de la electricidad del día siguiente. Su aplicación a los mercados de California y de España mostró errores medios inferiores al 10 %
En el caso que plantean Nogales et al. (2002), se realiza una regresión dinámica para predicción de precios. En este caso, los precios de una hora están relacionados con los valores pasados del precio y se utiliza un modelo de función de transferencia donde se asume que el precio y la demanda son estacionarios. Por su parte, Conejo et al. (2005) utilizan la Transformada de Wavelet y el modelo ARIMA para la predicción de precios en el corto plazo. En este caso, la serie histórica de precios se descompone al usar la Transformada de Wavelet, luego se pronostican los valores de la serie utilizando el modelo ARIMA. Las predicciones con ARIMA permiten, por medio de la Transformada inversa de Wavelet, reconstruir el comportamiento de las series de los precios. Otros autores como Botero y Cano (2008) han realizado predicción de precios por medio de series de tiempo con modelos de regresión con base en series históricas de precios. Asimismo, Weron y Misiorek (2005) estudian modelos con series de tiempo ARMA y ARMAX con entradas exógenas que se han utilizado en modelos con redes neuronales autorregresivas en el mercado eléctrico brasileño, como el reportado en Velásquez et al. (2008). En el modelo de red neuronal difusa, propuesto por Amjady (2006), se predicen los precios horarios, con un día de antelación, mediante una combinación de lógica difusa y un algoritmo de aprendizaje. Zhang (2003) ofrece una metodología híbrida que combina el modelo ARIMA con redes neuronales artificiales (ANN) para la predicción de precios de electricidad a corto plazo. Los resultados indicaron que un modelo híbrido ARIMA-ANN puede mejorar la precisión de las previsiones de precio. Por su parte, Catalão et al. (2011) presentan un enfoque híbrido que utiliza la Transformada de Wavelet, redes neuronales y lógica difusa para la predicción de precios en el corto plazo en un mercado eléctrico competitivo.
Según Franses (1999), los modelos GARCH (Generalized Autoregressive Conditional Heteroscedasticity) son de gran aceptación, debido a que permiten ajustar las dos principales características o hechos estilizados de los retornos financieros. A pesar de su versatilidad, los modelos GARCH parten del supuesto de que choques o noticias negativas afectan de la misma manera al retorno que choques o noticias positivas. Es decir, para estos modelos, el signo del choque es irrelevante, otro hecho empírico de gran peso en los retornos financieros asociados con la volatilidad.
García et al. (2005) describen un modelo generalizado condicional autoregresivo heterocedástico (GARCH) que permite analizar datos de series de tiempo en general, el cual es aplicado a la predicción de precios en el mercado español y californiano. Un estudio que utiliza una variedad de modelos estadísticos, univariados y multivariados, para la predicción de la volatilidad condicional de varios contratos de futuros sobre energía que cotizan en la Bolsa Mercantil de Nueva York, es el de Sadorsky (2006). De acuerdo con los resultados de la prueba estadística de predicción óptima, el modelo TGARCH presenta un desempeño superior para predecir la volatilidad condicional en los futuros sobre gas natural y aceite de calefacción. Por su parte, el modelo GARCH estándar tiene capacidad predictiva superior para estimar la volatilidad cambiante en el tiempo en los mercados de futuros sobre petróleo crudo WTI y gasolina, en comparación con el desempeño de los modelos de cambio de régimen, VAR y GARCH bivariados
En Colombia, los estudios y trabajos realizados como los de Velásquez et al. (2007); Grajales, (2009); Bello-Rodríguez y Beltrán-Ahumada (2010); Sierra y Castaño, (2010); González y Meza, (2011); Barrientos et al. (2012); García et al. (2013); Hurtado et al. (2014); Duarte y García, (2015) y Botero et al. (2016) presentan resultados bastante diversos. De pertinencia para este estudio, se toma el de Gil y Maya (2008), quienes propusieron un modelo EGARCH para modelar la volatilidad del precio diario de la energía en Colombia. En su trabajo, incorporaron factores como la estacionalidad de la serie, la demanda y el efecto del fenómeno de El Niño. Sin embargo, en el análisis realizado no se tuvo en cuenta la composición horaria de la serie, el comportamiento interno de esta, ni el cambio en el comportamiento de la volatilidad ante la presencia o no del fenómeno de El Niño. Asimismo, Arroyo (2010) propone un modelo GARCH para cada una de las horas de los precios de la energía en el mercado colombiano. Villada et al. (2011) y Agudelo et al. (2015), por su parte, realizan la predicción de precios de energía eléctrica en Colombia mediante el uso de redes neurodifusas. En este caso, se utilizaron dos estructuras de red; una tomó como entrada la serie de precios diarios y la segunda, la serie de precios diarios y el nivel medio de los embalses, con lo que se obtuvieron mejores resultados en el pronóstico con la última alternativa.
Barrientos et al. (2012) predicen el precio de la energía en Colombia a largo plazo con modelos de redes neuronales, considerando como variables de entrada la demanda y oferta de la electricidad y el nivel de los embalses. Anbazhagan y Kumarappan (2013) presentan un modelo de red neuronal recurrente para la predicción a corto plazo usando el modelo de red de Elman. Según los autores, este modelo puede obtener resultados similares a otros modelos de predicción como el ARIMA y redes neurodifusas en menor tiempo computacional.
Para el desarrollo del presente trabajo se contó con información disponible de precios de bolsa desde enero de 2004 hasta diciembre de 2016, publicados por la Compañía Expertos en Mercados (XM) en su página web, entidad encargada de la operación del Sistema Interconectado Nacional (SIN) y la administración del Mercado de Energía Mayorista Colombiano (MEM).
Después de esta introducción, la primera parte corresponde a la metodología donde se presentan los conceptos básicos de series de tiempo estacionarias, econometría de series de tiempo. La segunda parte corresponde al análisis y resultados del modelo para la predicción del precio de bolsa de la energía en Colombia, con el que, después de cumplir con las pruebas de rigor, se obtiene el modelo ARIMA con IGARCH. El artículo termina con las conclusiones.
1. Metodología
El uso de modelos para pronosticar es amplio y diverso, como en la planeación y control de operaciones, en la mercadotecnia, la economía, el sector financiero, estudios de capacidades, presupuestos, demografía, entre otros.
La variedad de casos de pronósticos evidencia la profundidad y amplitud de su campo. Antes de pronosticar una variable, se debe construir un modelo estimando parámetros y usando valores históricos observados. El modelo previsto arroja una caracterización estadística de los vínculos del presente y del pasado. En forma sencilla, de acuerdo con el pasado, se construye un modelo de pronóstico para lo que se espera, y se predice de forma calculada el futuro. Los datos observados y ordenados de manera secuencial, que muestran la tendencia en un gráfico son, por lo general, el primer paso para analizar una serie de tiempo. En este análisis se verifica la tendencia como la variación de los datos en el tiempo (Diebold, 2001), revisando sus patrones periódicos de comportamiento o estacionalidad (Montenegro, 2010); el comportamiento alrededor de la tendencia caracterizando los ciclos (Hanke & Wichern, 2003), que no necesariamente se comporta de manera regular y requiere modelos más complicados que los que incluyen tendencia o estacionalidad. Las técnicas que se utilizan cuando se pronostican series cíclicas consideran modelos de descomposición clásica, de indicadores económicos, econométricos, de regresión múltiple y ARIMA (métodos Box-Jenkins). Este efecto cíclico será el desarrollado en las siguientes secciones utilizando modelos de pronósticos ARIMA.
Las observaciones ordenadas en el tiempo son llamadas serie de tiempo; para pronosticar series de tiempo cíclicas la estructura probabilística básica de la serie no debe cambiar en el tiempo, debido a que las leyes que rigieron en el pasado serán diferentes a las del futuro. Luego, para pronosticar una serie, lo mínimo que debería cumplir es que su media y su covarianza sea estable en el tiempo.
Así, se tendrá que definir que para el análisis de serie de tiempo el proceso —sea estocástico estacionario (media y varianza constante en el tiempo), no estacionario (comportamientos aleatorios), de raíz unitaria (test alterno para identificar estacionariedad o integrados)— cuando una serie de tiempo no estacionaria debe diferenciarse d veces para convertirla en estacionaria, se dice que es integrada de orden d, en economía normalmente son estacionarias de orden 1. Una vez hecha la prueba gráfica para observar tendencias e identificar si es o no estacionaria, se procede a hacer pruebas más formales como la de función de autocorrelación (ACF) donde coeficientes de correlación altos identifican la no estacionariedad de la serie de tiempo. Elegir la longitud de rezago es un asunto empírico. Una regla consiste en obtener la ACF hasta una tercera o cuarta parte de los valores de la serie de tiempo. Es decir, si se tienen 100 observaciones, se tomarán solo 33 observaciones (Enders, 1995; Gujarati, 2003). Las pruebas de Raiz Unitaria y de Dickey-Fuller confirmarán o rechazarán las hipótesis de estacionariedad de las series de tiempo.
Para la escogencia del modelo, Gujarati (2003) postula cinco enfoques para la predicción basados en series de tiempo: (i) métodos de alisamiento exponencial, (ii) los modelos de regresión uniecuacionales, (iii) los modelos de regresión de ecuaciones simultáneas, (iv) los modelos autorregresivos integrados de media móvil (ARIMA) y (v) los modelos de vectores autorregresivos (VAR).
Box y Jenkins (1976) publican Time Series Analysis: Forecasting and Control imponiendo una nueva herramienta de pronóstico, esta herramienta, conocida como metodología de Box-Jenkins (BJ), hoy es identificada como metodología ARIMA. El acrónimo del inglés autoregressive integrated moving average procede de los siguientes elementos:
AR Proceso autorregresivo: proceso aleatorio para casos generales de variabilidad en el tiempo.
I Integrado: una serie de tiempo es integrada de orden 1 (es decir, I(1)) si sus primeras diferencias son estacionarias. En forma similar, si una serie de tiempo es I(2), su segunda diferencia es estacionaria. Por consiguiente, si se debe diferenciar una serie de tiempo d veces para hacerla estacionaria y luego aplicar un modelo ARMA (p, q), se dice que la serie es ARIMA (p, d, q), es decir, una serie de tiempo autorregresivo integrada de media móvil. Donde p son los términos autorregresivos, q los términos de media móvil y d, el número de veces que la serie de tiempo debe ser diferenciada para hacerla estacionaria.
MA (moving average) media móvil: que se calcula para suavizar la volatilidad de una serie de datos mediante el promedio de subconjuntos de la serie completa.
ARIMA tiene el énfasis en el análisis de las propiedades probabilísticas, o estocásticas de las series de tiempo. A diferencia de otros modelos de regresión, en que los Yt está pronosticada por la k regresoras X1, X2, X3,… Xk, en los modelos de Box-Jenkins Yt puede ser explicada por datos pasados o reza gada de sí misma, y por los coeficientes o términos estocásticos de error. La mayoría de series de tiempo son estacionarias en el sentido en que la media y la varianza son constantes y la covarianza es invariante en el tiempo. La mayoría de las series económicas no son estacionarias, por ello se requiere diferenciarlas.
Este documento estudiará los modelos ARIMA por tres razones principales: (i) fácil metodología, en donde se incluyen procesos matemáticos y estadísticos, (ii) la aplicación empírica que tienen estos modelos para inferir a partir de situaciones muéstrales y (iii) estos modelos han demostrado una eficiencia en la predicción de las series en el corto plazo.
Los modelos ARIMA no consideran a las variables independientes en su construcción, emplean información que se encuentra en la misma serie para generar los pronósticos. Los modelos ARIMA dependen de los patrones de autocorrelación que existen en los datos (Hanke & Wichern, 2003).
El objetivo de la metodología de Box Jenkins (BJ) es identificar y estimar un modelo estadístico que pueda ser interpretado como generador de la información muestra. Si el modelo estimado se utilizará para predicción, debe suponerse que sus características son constantes en el tiempo y en particular en el futuro (Gujarati, 2003).
El método Box-Jenkins utiliza una estrategia iterativa para construir los modelos, que consiste en seleccionar un modelo inicial mediante la estimación de los coeficientes del modelo y el análisis de los residuales. Si es necesario, el modelo inicial se modifica y el proceso se repite hasta que los residuales indiquen que no es necesario seguir modificando. Finalmente, el modelo ajustado se utiliza para el pronóstico. El método considera cuatro pasos, como se muestra en la figura 1.
Para seleccionar un modelo ARIMA, se parte de un modelo de pocos parámetros, la necesidad de parámetros adicionales será evidente con un análisis de las autocorrelaciones residuales y de autocorrelaciones parciales. Por otra parte, si los parámetros de un modelo ARIMA no son significativos, será necesario ir anulando parámetro por parámetro a la vez y ajustando el modelo.
Si dos modelos iniciales pueden ser coherentes y los dos contienen el mismo número de parámetros, se escogerá el modelo con el menor error cuadrático medio. Si los modelos tienen diferente cantidad de parámetros por el principio de parsimonia 1 (Hanke & Wichern, 2003), se seleccionará el más sencillo, aunque es probable que el modelo con más parámetros tenga un error cuadrado medio más pequeño.
Las series de tiempo a menudo presentan el fenómeno de acumulación de la volatilidad; es decir, presentan lapsos en los que sus valores muestran grandes variaciones durante prolongados periodos y luego se dan intervalos en los que hay una calma relativa (Gujarati, 2003). Conocer la volatilidad resulta crucial en los pronósticos. En las primeras diferencias aún continúa presentándose la volatilidad, lo que sugiere que la varianza de las series de tiempo se modifica con el tiempo o, más aun, es cuando se podrían aplicar los modelos de heterocedasticidad condicional autorregresivo (ARCH) desarrollado por Robert Engle en 1982.
El modelo ARCH puede ser una aproximación a un sistema más complejo con referencia a modelos donde la varianza es constante. Casi siempre los modelos estructurales admiten una especificación tipo ARCH que se halla con variables cambiantes, lo que la resalta como principal característica de estos modelos porque son capaces de contrastar la hipótesis de permanencia estructural que suponen los modelos econométricos tradicionales.
En conclusión, el factor clave de los modelos ARCH es que consideran los datos de información históricos de la variable y su volatilidad como la clave altamente probable de la explicación de su comportamiento presente y su futuro.
Se define un proceso estocástico estacionario como aquella sucesión ordenada de variables aleatorias cuya función de distribución no varía en una serie de valores igualmente espaciados.
En cuanto al modelo GARCH, del inglés Generalized Autorregresive Conditional Heterocedasticity, no es más que el reflejo del trabajo de Bolleslev (1986) para la ampliación del modelo ARCH en los órdenes (p, q) y de Taylor (1986) para los órdenes (1,1).
La modelación del GARCH se enfoca en el análisis que trata el exceso de curtosis y la volatilidad. Estas características proporcionan una adecuada predicción de las varianzas y las covarianzas del retorno de los activos por medio de su facilidad para modelar la variación en el tiempo de las varianzas condicionales.
El proceso GARCH (heterocedasticidad condicional autorregresiva generalizado) es un modelo simétrico que actúa como un mecanismo adaptativo que tiene en cuenta la varianza condicionada en cada etapa de una serie.
La modelación IGARCH estima la varianza teniendo en cuenta que esta es integrada por medio de una estimación de máxima verosimilitud que se distribuye como una t-student con grados de libertad.
2. Análisis y resultados
Para el modelo seleccionado se presenta el diagrama de flujo (figura 2) para encontrar el modelo que mejor se ajuste a las condiciones requeridas del trabajo de predicción de precios de bolsa.
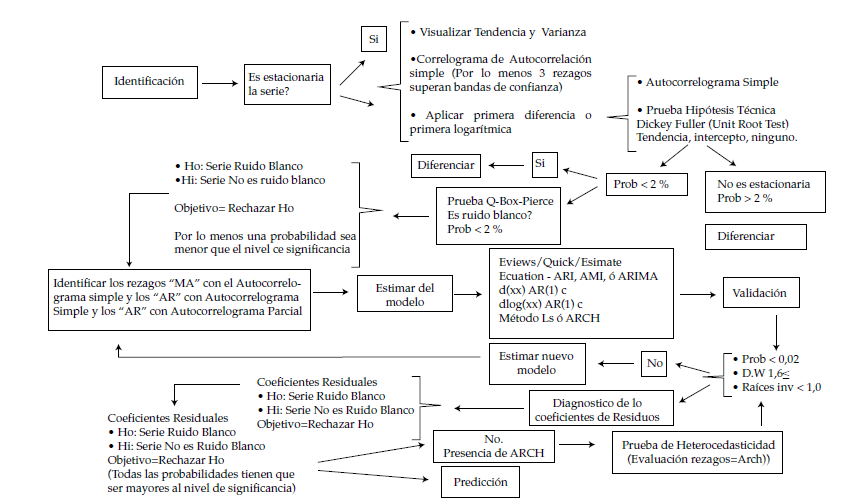
La serie que se trabajó para crear este modelo se obtuvo de la página web de la compañía colombiana Expertos en Mercados (XM) (s.f.) filial del grupo ISA, la cual se encarga de la operación del Sistema Interconectado Nacional (SIN) y la administración del Mercado de Energía Mayorista (MEM). La serie está creada con base en el valor promedio de los treinta días de cada mes desde el mes de enero de 2004 hasta diciembre de 2016. En la figura 4 se ilustra la serie de precios de energía colocando en el eje vertical el precio mensual de energía en $/kWh y en el eje horizontal los años.
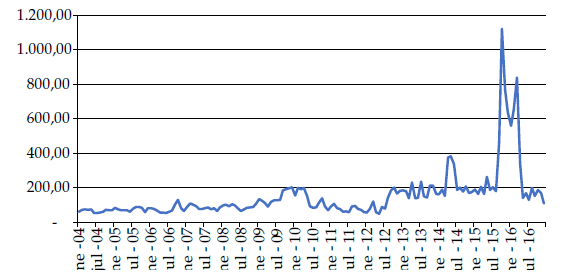
Gráficamente, se puede observar que la serie original no es estacionaria y que tiene tendencia y variabilidad, por lo que se tiene que descartar cualquier posibilidad de constituir un modelo de pronóstico tipo ARMA. Por lo anterior, es necesario transformar la serie de tiempo original a diferencia regular o logarítmica, lo que implica la necesidad de un proceso de integración y posibilita la constitución de un modelo ARIMA o, por ejemplo, ARI o IMA.
Las transformaciones de datos tratan de estabilizar la media y la varianza de la serie. Las series económicas muestran una variabilidad que depende de la media, siendo en ese caso la transformación logarítmica la más adecuada. La transformación logarítmica tiene distintas ventajas estadísticas ya que:
Independiza la varianza de la media.
Induce normalidad en los datos, y linealiza las relaciones.
Al prever una variable a partir de su logaritmo, las previsiones serán positivas.
Al ser una serie de precios, se opta por la diferencia logarítmica del precio de bolsa de energía mensual, con lo que se obtiene la serie de tiempo transformada (figura 5), utilizando el programa E-Views:
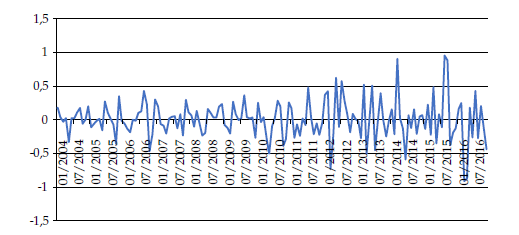
A simple vista, parece que se eliminaron los problemas de tendencia y variabilidad de la serie. Sin embargo, como es bien conocido, es necesario comprobar que la serie es idónea para pronóstico, al verificar, primero, que sea estacionaria, mediante la prueba de Dickey-Fuller y, segundo, que no sea ruido blanco, por medio de la prueba Q-Box-Pierce. El hecho de que la serie no presente ruido blanco quiere decir que las observaciones pasadas influyen sobre el comportamiento en los siguientes periodos, en pocas palabras, que la serie tiene memoria y, por ende, garantiza que se puedan encontrar los patrones de comportamiento para la construcción del respectivo modelo de pronóstico.
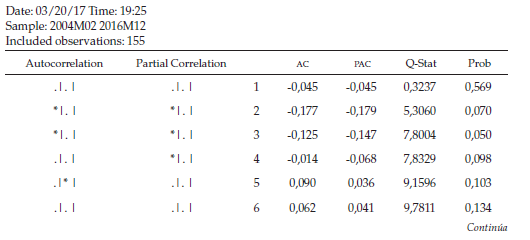
En seguida, se realiza el correlograma simple para comprobar adicionalmente si la serie es o no estacionaria. Se aprecia por medio del correlograma de autocorrelación simple (tabla 1) que la serie es estacionaria. Ahora, se procede de manera técnica por medio de la prueba Dickey-Fuller Aumentada, que corresponde a una prueba de hipótesis la cual permite validar si la serie es estacionaria y con ello reconfirmar lo evidenciado en el Correlograma de Autocorrelación Simple.
La prueba de hipótesis para comprobar la estacionariedad es la siguiente:
Donde, t-1 es el orden del rezago, μt es el Ruido Blanco, Ho es la Hipótesis Nula que dice que la serie no es estacionaria dado que tiene raíz unitaria, ρ = 1 y Hi es ρ ≠ 1. La serie es estacionaria; el objetivo es rechazar la Hipótesis Nula.
El tao debe ser negativo y para rechazar la hipótesis nula de no estacionariedad se necesita que ôτc ô ≻ τ* . La manera alternativa para observar si el estadístico de prueba es significativo es identificar la probabilidad desde -∞ hasta el valor tao y compararlo con el nivel de significancia definido por el investigador, que para este caso será definido al 2 %. La regla de decisión será, por lo tanto, que la probabilidad de este valor sea menor o igual al 2 % con el fin de rechazar la hipótesis nula y garantizar que la serie sea estacionaria.
Para verificar tal hipótesis, se corre la prueba de raíz unitaria ADF en Eviews (ver tabla 2).
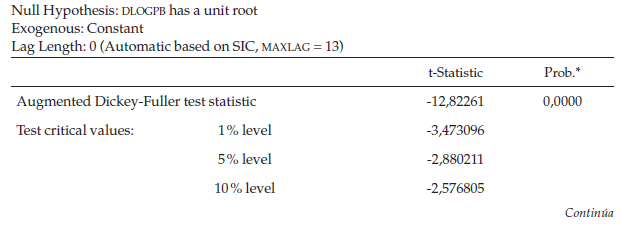
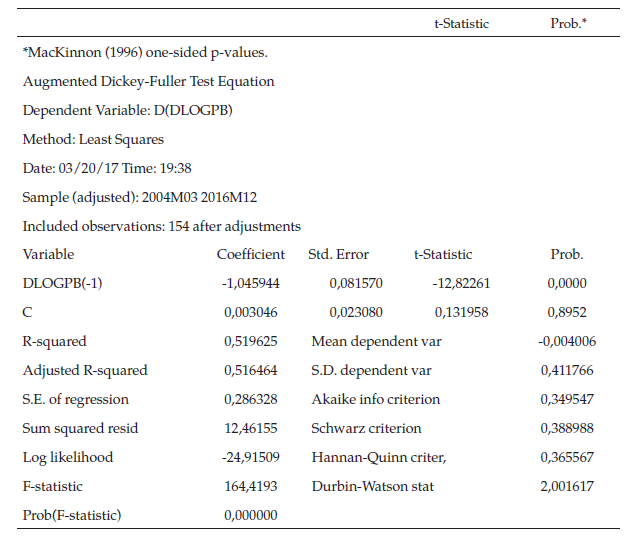
Al realizar la prueba Dickey-Fuller ampliada, sin tendencia e intercepto, cuya ecuación es la mejor que se adapta a la primera diferencia logarítmica, se observa que la serie es estacionaria con un Tao calculado de -10,72147, que es menor al valor crítico de -2,58 y que establece el nivel del 2 %. Una forma alternativa para tomar la decisión es observar el p-value frente al nivel de significancia, en este caso se aprecia que la probabilidad o p-value del estadístico de prueba es menor al nivel de significancia y por tal motivo se rechaza la hipótesis nula y se garantiza la estacionariedad de la serie.
El siguiente paso es determinar que la serie estacionaria no sea ruido blanco, es decir, que no tenga memoria (en caso de tener memoria su mejor pronóstico es el dato más reciente), y se realiza por medio de la prueba Q de Box-Pierce. Donde se plantea la prueba de Hipótesis Nula que establece que la serie es ruido blanco frente a la Hipótesis Alterna que los datos no son ruido blanco:
H 0 = p 1 = p 2 = , …, p 2 = 0 ;
Hi = p 1 ≠ p 2 ≠ , …, p 2 ≠ 0 ;
El objetivo es rechazar la Hipótesis Nula.
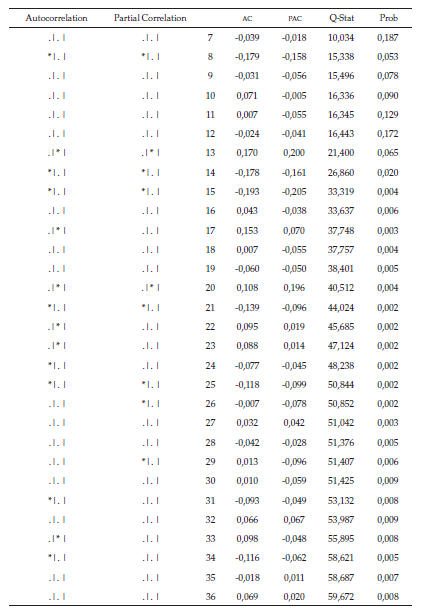
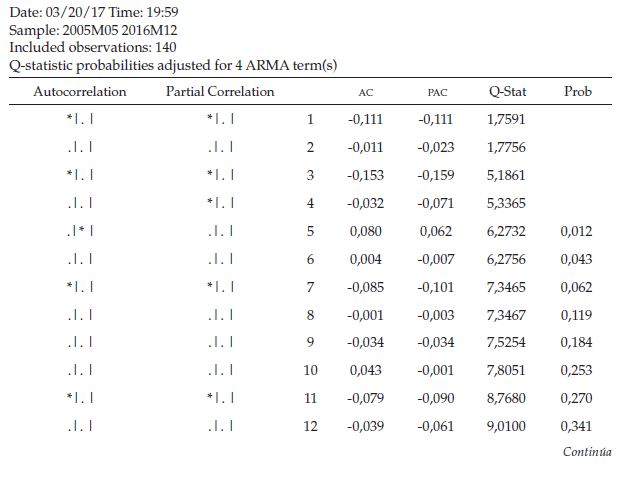
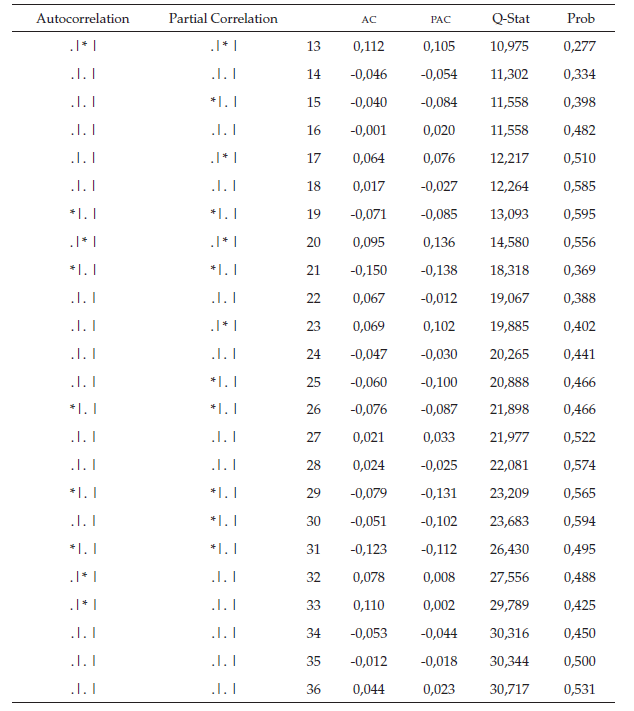
Esto se logra cuando al menos una probabilidad debe ser menor al nivel de significancia del 2 %. Lo anterior se valida con el correlograma de la serie de tiempo transformada (tabla 3), en la primera diferencia logarítmica donde en las dos últimas columnas se muestra el estadístico Q de Box-Pierce junto con su respectivo p-value para cada uno de los rezagos respectivos.

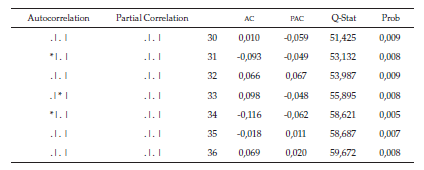
La parte correspondiente a los valores probabilísticos (prob), resaltada en color gris, ratifica que se rechaza la hipótesis nula y que la serie no es ruido blanco, ya que al menos una probabilidad debe ser menor al nivel de significancia, por tal motivo se confirma que la serie estacionaria no es ruido blanco.
El siguiente proceso es determinar cuáles son los procesos autorregresivos y los procesos de media móvil que genera el patrón de comportamiento de la serie. Los procesos autorregresivos (AR) se identifican con el correlograma de autocorrelación parcial (Partial correlation), y los procesos de media móvil (MA) se identifican con el correlograma de autocorrelación simple (autocorrelation).
Como se observa en la tabla 3 de la serie de diferencias logarítmicas, la serie no es ruido blanco y tiene procesos autorregresivos de orden 2 y de media móvil fuertes en los rezagos 2, 8, 13, 14 y 15.
Después de haber establecido los patrones de comportamiento, ahora se iniciaría la construcción de un modelo de pronóstico, considerando que el correlograma indicó que se tienen procesos autorregresivos y de media móvil en los rezagos respectivos. Después de varias pruebas, se presenta en la tabla 4 el modelo MA (8) AR (8) MA (15) MA (14), sin intercepto y con orden IGARCH (1,1) evaluado en la aplicación de Eviews.
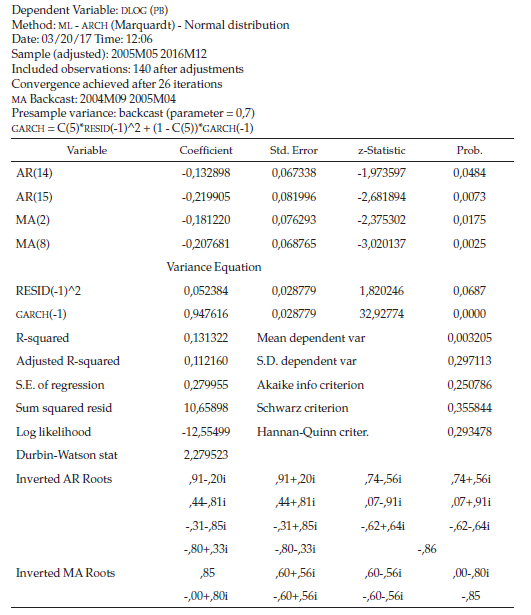
Seguidamente, se presentan todas las hipótesis individuales a implementar con un nivel de significancia del 7 %, donde se ratifica la significancia tanto de los parámetros que acompañan el modelo ARIMA y el modelo IGARCH, a medida que se avance en la validación del modelo.
De manera general, se presenta la respectiva prueba que se realiza para cada uno de los parámetros.
Hi = ϕi ≠ 0
H 0 = ϕi =0
De acuerdo con lo apreciado en la tabla 4, se observa que las probabilidades resaltadas en gris son menores al nivel de significancia establecido del 7 %. Por tal motivo, se garantiza que los parámetros son significativos. Todas las raíces invertidas son menores a uno en valor absoluto, por lo que no hay sobrestimación de parámetros y se garantiza la convergencia de la serie a su media de largo plazo, además, el valor del estadístico de Durbin-Watson es de 2,27, muy cercano a 2, lo que garantiza la no autocorrelación entre los errores de periodo “t” y los errores del periodo “t-1”.
Es necesario, después de validar los coeficientes, determinar si los errores del modelo establecido son ruido blanco con el fin de garantizar que no existen otros procesos de media móvil que puedan afectar las interacciones realizadas en el modelo identificado anteriormente. El estadístico Q de Box Pierce permite establecer si los errores son o no ruido blanco y se plantea la Hipótesis Nula que establece que los errores son ruido blanco frente a la Alterna que corresponde a la negación de la Hipótesis Nula de que los errores no son ruido blanco:
H 0 = p 1 = p 2 = , …, p 2 = 0 ;
Hi = p 1 ≠ p 2 ≠ , …, ; p 2 ↑ 0
El objetivo corresponde a no rechazar la Hipótesis Nula.
Esto se logra cuando todas las probabilidades son mayores al nivel de significancia del 2 %.
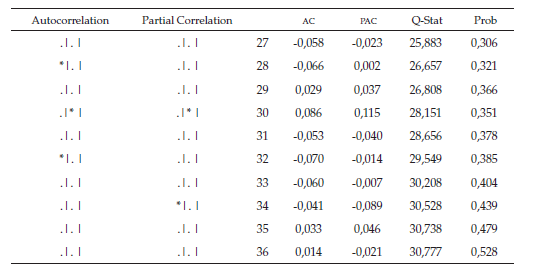
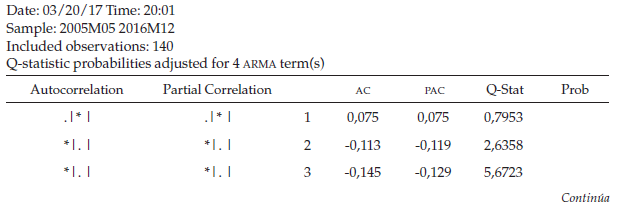
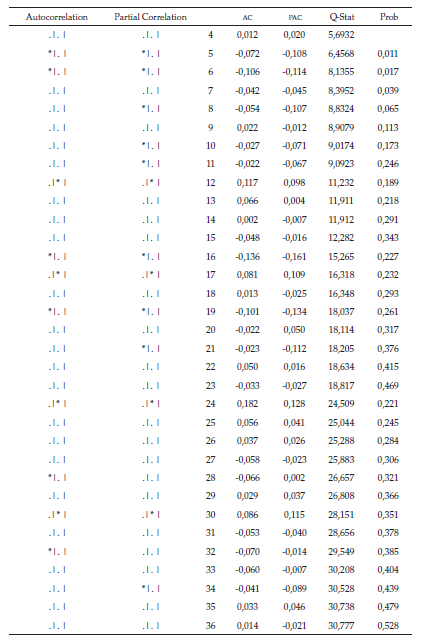
Al observar el correlograma de los residuos (tabla 5), se puede determinar que el error es ruido blanco, ya que todos los rezagos se ubican dentro de la banda y las probabilidades son superiores al nivel de significancia en todos los rezagos.
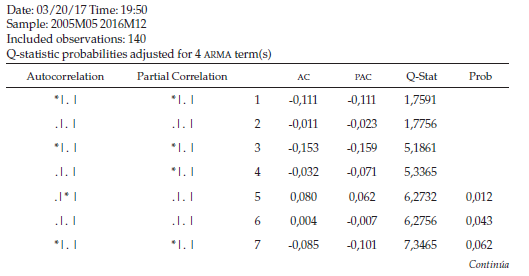
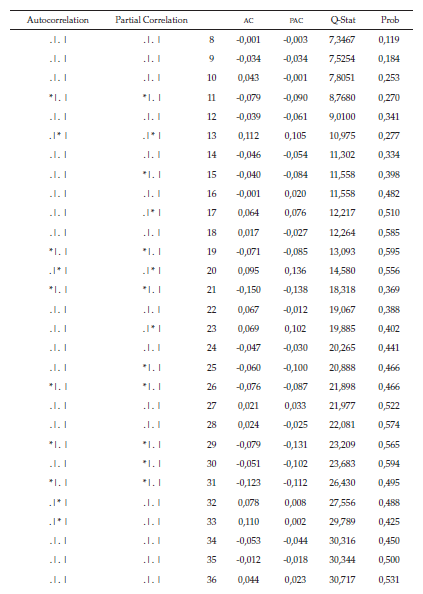
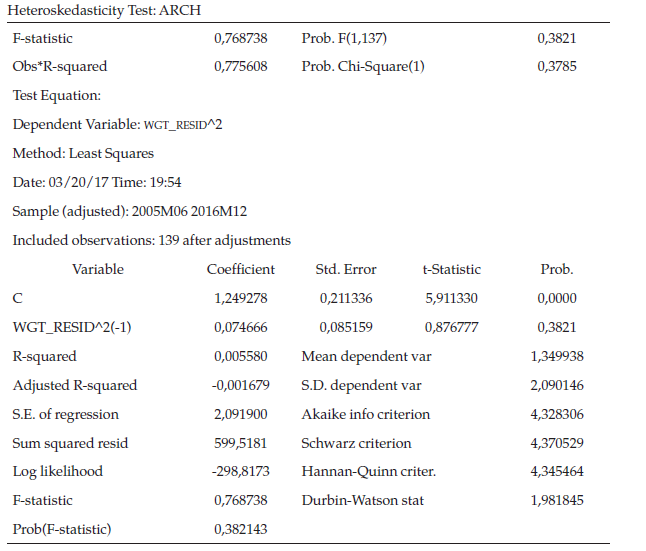
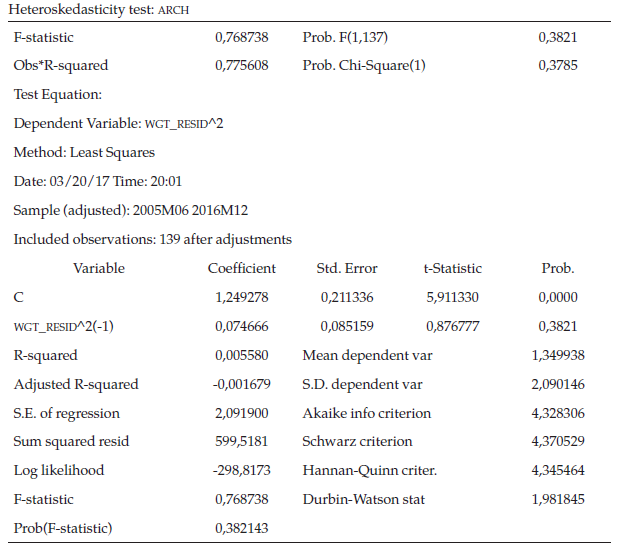
De acuerdo con el correlograma de los residuos al cuadrado (tabla 6), se determina que los errores al cuadrado no son ruido blanco debido a que no todas las probabilidades son mayores al nivel de significancia, para garantizar si existe presencia del efecto ARCH se procede a realizar la respectiva prueba de hipótesis donde el estadístico de prueba R2 se distribuye con una JI-Cuadrado con k grados de libertad.

La regresión auxiliar que permite generar el estadístico de prueba descrito anteriormente es:
Donde, Vt es ruido blanco.
La hipótesis Nula plantea que todos los coeficientes son simultáneamente iguales a cero, es decir, no hay presencia del efecto ARCH frente a una Hipótesis Alterna de que al menos un coeficiente es diferente de cero, o sea que existe la presencia del efecto ARCH.
Después de realizar distintas estimaciones, los efectos de heterocedasticidad condicional ARCH, GARCH y sus derivaciones (tabla 7), se presenta en la tabla 8 el respectivo modelo definitivo donde se aprecia que los coeficientes de media móvil y los coeficientes del modelo de volatilidad de la energía son significativos. Adicionalmente, se muestran las salidas en Eviews garantizando que los residuos y los residuos al cuadrado de este modelo iterativo son ruido blanco y además se realiza la prueba ARCH y esta ratifica que no hay presencia del efecto ARCH. Con base en estos resultados se establecerá el pronóstico para el mes de enero de 2017 de la serie objeto de estudio.
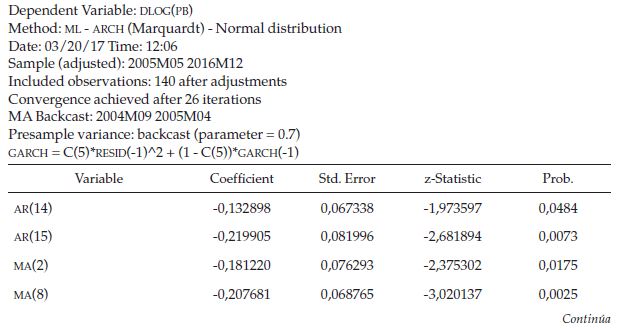
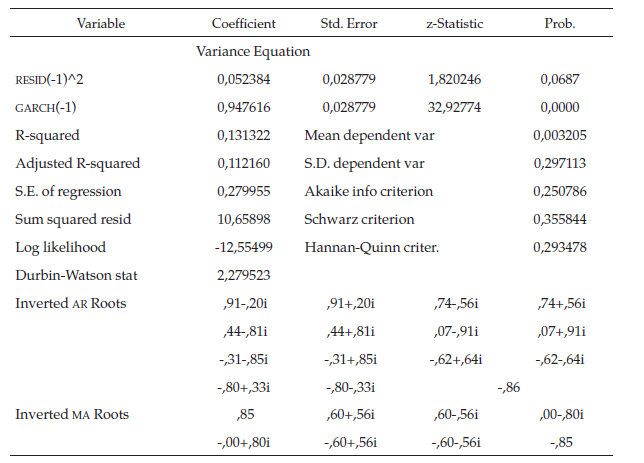
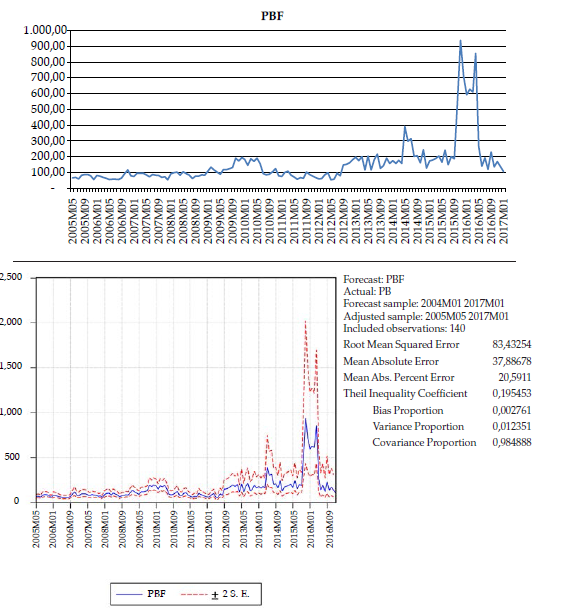
Con base en el modelo encontrado, se procede a realizar el respectivo pronóstico del precio de la energía para el mes de enero de 2017 y el valor arrojado es de 106,40 $/kWh. El precio promedio de bolsa real de energía en ese mes correspondió a 111 $/kWh, lo que conlleva a que el desfase del modelo con el valor real es de $4,6 y en términos porcentuales de un 4 %, aproximadamente.
El Theil Inequality Coefficient (figura 6) es un indicador que garantiza si el modelo establecido está estructurado para generar un buen pronóstico y se encuentra dentro de un rango de 0 a 1. De acuerdo con los resultados obtenidos, el coeficiente fue 0,19; muy cercano a cero, lo cual garantiza que el cálculo del pronóstico se realiza bajo la construcción de un modelo robusto.
3. Conclusiones
A mediados de la década de los noventa, la liberación y desregulación de los mercados de energía eléctrica en Colombia, dados en las Leyes 142 y 143 de 1994 (Ley de Servicios Públicos y Ley Eléctrica), eliminaron el monopolio estatal en el sector eléctrico e introdujeron la competencia en el sector, esto se organizó por actividades: generación, transmisión, distribución y comercialización de energía. Se estableció el sistema de Bolsa de Energía, el cual centralizó las operaciones de compra y venta de energía para abastecer la demanda y en el cual participan activamente agentes generadores y comercializadores del país.
Los agentes generadores que representan a la oferta de energía hacen su oferta en bolsa, la cual consiste en declarar diariamente la disponibilidad y el precio de la energía. De acuerdo con la normatividad, los precios de los agentes generadores en Colombia deben ser el resultado de la estimación de los costos variables de generación, que para las plantas hidráulicas están dados por el costo de oportunidad del agua, y para las plantas termoeléctricas los costos de combustibles más los costos de administración operación y mantenimiento.
En las plantas hidroeléctricas, el costo de oportunidad del agua está definido principalmente por la hidrología del país y es el resultado de la decisión de utilizar o no el agua para generar energía. Este dilema es parte del riesgo que deben asumir estos generadores, pues causan volatilidad en dichas ofertas lo que termina afectando de manera directa la formación de precio de bolsa, ya que los generadores hidroeléctricos superan a los termoeléctricos en una relación de 70:30.
El pronóstico de una serie de precios de energía es una tarea difícil y compleja por estar presente diferentes niveles de estacionalidad y la presencia de variables exógenas, especialmente las relacionadas con el clima. Al ser el precio de la energía una variable afectada por otras de tipo cuantitativo y cualitativo (regulaciones CREG, tecnología y hábitos en la población) serían estos últimos aspectos los más complejos para involucrarlos en un modelo regresivo de pronóstico. Es así como se ha considerado utilizar los modelos univariantes llamados ARIMA; es decir, que los propios datos temporales históricos de la variable estudiada indican la estructura probabilística y el patrón teórico de comportamiento.
La ventaja de un modelo ARIMA radica en que no requiere otras series de datos referidas al mismo periodo, y ahorra la identificación y especificación del modelo aplicando econometría tradicional. El modelo desarrollado para pronosticar el precio de energía del mes de enero de 2017 dio como resultado un MA (8) AR (8) MA (15) MA (14) sin intercepto con un IGARCH (1,1).
Un modelo ARIMA es dinámico y de corto plazo, toda vez que para pronosticar el valor de febrero de 2017 debe alimentarse la serie con el valor hallado por el modelo de enero de 2017. Este valor pronosticado de enero se convierte en un valor histórico, con el que se genera medias, varianzas, correlogramas y coeficientes diferentes antes de su ingreso a la serie original mensual de enero de 2004 a diciembre de 2016, siendo necesario iterar para identificar, estimar, verificar y así encontrar un nuevo modelo autorregresivo integrado de media móvil con IGARCH y predecir el periodo de febrero de 2017. Para los siguientes meses del año 2017 se repite el procedimiento anterior convirtiendo sucesivamente el valor pronosticado del mest-1 en un dato histórico, para generar finalmente el pronóstico de todos los meses del año 2017 y sus respectivos modelos ARIMA con su respectivo modelo de volatilidad condicional.
El modelo encontrado establece que si en las variables de estudios presentan ciertas características como comportamientos bruscos en periodos cortos de tiempo (alta volatilidad ocasionada por El Niño y La Niña), asimetría en su distribución y no cumple con los supuestos de estacionariedad, entre otros hechos, es preferible aplicar los modelos ARCH, GARCH y sus derivaciones por cubrir mejor la heterocedasticidad (varianza no constante).
Cabe agregar que la intervención del mercado eléctrico impuesta en octubre de 2015 por la Comisión de Regulación de Energía y Gas (CREG) (Min-Minas, 2015) le introdujo variables a la señal de precio, ya que se creó un techo artificial que no obedeció a ninguna variable de mercado y que sería imposible de predecir con cualquier modelo. Esto le agrega un mayor grado de complejidad a cualquier estudio que se haga sobre los precios de la energía en bolsa en Colombia.
Referencias
Agudelo, A., Lopez-Lezama, J., & Velilla, E. (2015). Predicción del Precio de la Electricidad en la Bolsa mediante un Modelo Neuronal No-Lineal Autorregresivo con Entradas Exógenas. Información Tecnológica, 26(6), 99-108.
Amjady, N. (2006). Day-Ahead Price Forecasting of Electricity Markets by a New Fuzzy Neural Network. IEEE Transactions on Power Systems, 21(2), 87-896.
Anbazhagan, S., & Kumarappan, N. (2013). Day-Ahead Deregulated Electricity Market Price Forecasting Using Recurrent Neural Network. IEEE Systems Journal, 7(4), 866-872.
Arroyo-Madera, Y. (2010). Modelos de análisis de series de tiempo (ARIMA y GARCH) aplicado a los precios de la bolsa de energía. Bogotá: Universidad de los Andes.
Barrientos, J., Rodas, E., Velilla, E., Lopera, M., & Villada, F. (2012). Modelo para el pronóstico del precio de la energía eléctrica en Colombia. Lecturas de Economía, 77, 91-127.
Bello-Rodríguez, S., & Beltrán-Ahumada R. (2010). Caracterización y pronóstico del precio spot de la energía eléctrica en Colombia. Revista Maestría en Derecho Económico, 6(6), 293-316.
Benini M., Marracci M., Pelachi P., & Venturini, A. (2002). Day-ahead Market Price Volatility Analysis in Deregulated Electricity Markets. IEEE Power Engineering Society Summer Meeting, 3, 1354-1359.
Bollerslev, T. (1986). Generalized Autoregressive Conditional Heteroskedasticity. Journal of Econometrics, 31, 307-327.
Botero, J., García, J., & Velásquez H. (2016). Efectos del cargo por confiabilidad sobre el precio spot de la energía eléctrica en Colombia. Cuadernos de Economía, 68, 491-519.
Botero, S., & Cano, J. A. (2008). Análisis de series de tiempo para la predicción de los precios de la energía en la bolsa de Colombia. Cuadernos de Economía, 48, 174-208.
Box, G., & Jenkins G. (1976). Time Series Analysis: Forecasting and Control Second Edition. San Francisco, C.A.: Holden Day.
Catalão, J., Pousinho, H., & Mendes, V. (2011). Short-term electricity prices forecasting in a competitive market by a hybrid intelligent approach. Energy Conversion and Management, 52, 1061-1065.
Compañía Expertos en Mercados (s.f.) Indicadores Energéticos. Disponible en http://www.xm.com.co/Pages/Home.aspx
Conejo, A., Plazas, M., Espínola, R., & Molina A. (2005). Day-Ahead Electricity Price Forecasting Using the Wavelet Transform and ARIMA Models. IEEE Transactions on Power Systems, 20(2), 1035-1042.
Contreras J., Espínola, R., Nogales, F., & Conejo, A. (2003). ARIMA Models to Predict Next-Day Electricity Prices. IEEE Transactions on Power Systems, 18(3), 1014-1020.
Diebold, F. (2001). Elementos de pronósticos. México: International Thomson Editores.
Duarte, O., & García, J. (2015). Estimación del precio marginal del sistema eléctrico colombiano: una mirada desde la organización industrial. Ecos de Economía, 19(41), 1-23.
Enders W. (2014). Applied Econometric Time Series, 4th Edition. New York: Wiley.
Engle, R. (1982). Autoregressive Conditional Heteroskedasticity with Estimates of the Variance of U.K. Inflation. Econometrica, 50(4), 987-1008.
Franses, P. (1999). Nonlinear time series models in empirical finance. Cambridge: Cambridge University Press.
García, J., Bohórquez, S., López, G., & Marín, F. (2013). Poder de mercado en mercados spot de generación eléctrica: metodología para su análisis. Documentos de trabajo. Economía y Finanzas, 13-05.
García, R., Contreras, J., & Van Akkeren, M. (2005). A GARCH forecasting model to predict day-ahead electricity prices. IEEE Transactions on Power Systems, 20(2), 867-874.
Gil, M., & Maya C. (2008). Volatility modeling of electric power prices in Colombia. Revista Ingeniería Universidad de Medellín, 7(12), 87-114.
González, L., & Meza, M. (2011). Análisis del Comportamiento del Precio Spot de la Energía en Colombia. (Tesis de Grado, Universidad Industrial de Santander, Colombia).
Grajales, D. (2009). Modelación del precio de la energía en Colombia usando un modelo de inferencia neurodifuso (anfis). Revista Soluciones de Postgrado EIA, 3, 25-38.
Gujarati, D. (2003). Econometría. México: Mc Graw-Hill International. Hanke, J., & Wichern, D. (2003). Pronósticos en los Negocios. 8.° edición. México: Pearson Prentice Hall.
Hurtado, L., Quintero O., & García, J. (2014). Estimación del precio de oferta de la energía eléctrica en Colombia mediante inteligencia artificial. Revista de Métodos Cuantitativos para la Economía y la Empresa, 18, 54-87.
Jakaša T., Andročec I., & Sprčić, P. (2011). Electricity price forecasting - ARIMA model approach. 8th International Conference on the European Energy Market (EEM). 25-27 May 2011. Zagreb, Croatia.
Lucia, J., & Schwartz E. (2002) Electricity Prices and Power Derivatives: Evidence from the Nordic Power Exchange. Review of Derivatives Research, 5, 5-50.
Ministerio de Minas y Energía (MinMinas) (2015). Comisión de Regulación de Energía y Gas Resolución No. 180 de 2015. Disponible en: http://apolo.creg.gov.co/Publicac.nsf/1c09d18d2d5ffb5b05256eee00709c02/1fefba75d3441a8305257f1b0077a8d1?OpenDocument
Montenegro, A. (2010). Análisis de series de tiempo. Bogotá: Pontificia Universidad Javeriana.
Nogales, F., Contreras, J., Conejo A., & Espínola, R. (2002). Forecasting nextday electricity prices by time series models. IEEE Transactions on Power Systems, 17(2), 342-348.
Pilipovic, D. (1997). Valuing and Managing Energy Derivatives. New York: McGraw-Hill.
Sadorsky, P. (2006). Modeling and forecasting petroleum futures volatility. Energy Economics, 28, 467-488.
Sierra, J., & Castaño, E. (2010). Pronóstico de precios spot del mercado eléctrico colombiano con modelos de parámetros variantes en el tiempo y variables fundamentales. VII Coloquio Regional de Estadística: Estadística Aplicada: “Didáctica de la Estadística y Métodos Estadísticos en Problemas Socioeconómicos” Universidad Nacional de Colombia.
Taylor, S. (1986). Modelling Financial Time Series. New York: Wiley.
Velásquez J., Dyner I., & Castro R. (2007). ¿Por qué es tan difícil obtener pronósticos de los precios de la electricidad en los mercados competitivos? Cuadernos de Administración, 259-282.
Velásquez, J., Dyner, I., & Souza, R. (2008). Modelado del precio spot de la electricidad en Brasil usando una red neuronal autorregresiva. Revista Chilena de Ingeniería, 16(3), 394-403.
Villada, F., García, E., & Molina, J. (2011). Pronóstico del Precio de la Energía Eléctrica usando Redes Neuro-Difusas. Información Tecnológica, 22(6), 111-120.
Weron, R., & Misiorek, A. (2005). Forecasting spot electricity prices with time series models. The European Electricity Market EEM, 05, 133-141.
Zhang, P. (2003). Time Series Forecasting Using a Hybrid ARIMA and Neural Network Model. Neurocomputing, 50, 159-175.
Notas
1 Este precepto se refiere a la preferencia de modelos más simples sobre los complejos.
Notas de autor
* Docente/Investigador, Escuela de Negocios, Universidad del Norte. Magíster en Economía Empresarial, INCAE. Especialista en Finanzas y Administrador de Empresas, Universidad del Norte. Correspondencia: Km 5 antigua vía a Puerto Colombia - Atlántico, Colombia. Teléfono: 350 9509 Ext. 4022. Correo electrónico: amunoz@uninorte.edu.co
† Magíster en Finanzas, Universidad del Norte. Especialista en Finanzas, Universidad del Norte. Ingeniero Electricista, Universidad del Norte. Correo electrónico: jurquijo@yahoo.com
‡ Magíster en Administración de Empresas, Universidad del Norte. Magíster en Finanzas, Universidad del Norte. Especialista en Finanzas, Universidad del Norte. Ingeniero Electricista, Universidad del Norte. Correo electrónico: anibalcot@gmail.com
§ Docente/Investigador, Escuela de Negocios, Universidad del Norte. Ph. D. en Economía, Universidad de Goettingen. Magíster en Estudios Internacionales, Universidad de Chile. Economista, Universidad del Rosario. Correo electrónico: lombanaj@uninorte.edu.co