
ISSN:0123-5362 | eISSN:2145-454X



A Widening Gap? A Gender-Based Analysis of Performance on the Colombian High School Exit Examination*
¿Una brecha que se amplía? Un análisis de la brecha de género en las pruebas desalida del colegio en Colombia
Uma brecha que se amplia? Uma ánalise da brechade gêneronas provas do ensino médio na Colômbia
Luz Karime Abadía, Gloria Bernal
A Widening Gap? A Gender-Based Analysis of Performance on the Colombian High School Exit Examination*
Revista de Economía del Rosario, vol. 20, no. 1, 2017
Universidad del Rosario
Luz Karime Abadía labadia@javeriana.edu.co
Pontificia Universidad Javeriana, Colombia
Gloria Bernal † gbernal@javeriana.edu.co
Pontificia Universidad Javeriana, Colombia
Received: September 27, 2016
Accepted: June 12, 2017
Additional information
Citethis article: Abadía, L K., & Bernal, G. (2016). A Widening Gap? A Gender-Based Analysis of Performance on the Colombian High School Exit Examination. Revista de Economía del Rosario, 20(1), 5-31. Doi: https://doi.org/10.12804/revistas.urosario.edu.co/economia/a.6144
Abstract:
In this article, we provide evidence that girls under perform boys with similar characteristics on the Colombian high school exit examination. Using the quantile regression technique, we find a significant gender gap favoring boys, which widens along the distribution. The Juhn-Murphy-Pierce decomposition shows that personal, family, and school characteristics explain a small part of the gap where as differences in returns play an important role. In addition, we show that the observed gap differs significantly by administrative regions, suggesting that specific characteristics of each region could be influencing girls’ performance.
JEL Classification: A14, A21, C21
Keywords: Gender gap, exit examination, Juhn-Murphy-Pierce descomposition.
Resumen:
En este artículo proveemos información sobre el menor desempeño de las niñas comparado con niños de similares características en las pruebas de salida del bachillerato colombianas, que son requeridas para el acceso a la Universidad. Usando la técnica de regresión cuantílica se encuentra que hay una brecha significativa a favor de los niños, que se incrementa a lo largo de la distribución. La descomposición de Juhn-Murphy-Pierce, muestra que las características personales, familiares y escolares explican una porción pequeña de las brechas, mientras que diferencias en los retornos juegan un papel importante. Adicionalmente, se muestra que la brecha observada difiere significativamente de acuerdo con la región; sugiriendo que características específicas de cada región como por ejemplo diferencias en la cultura relacionadas con el rol de la mujer pueden estar influenciando el desempeño de las niñas.
Clasificación JEL: A14, A21, C21
Palabras clave: brecha de género, exámenes estandarizados, descomposición Juhn-Murphy-Pierce.
Resumo:
Neste artigo provemos informação sobre o menor desempenho das meninas comparado com os meninos de similares característica nas provas colombianas de saída do ensino secundário, que são requeridas para o acesso à Universidade. Usando a técnica de regressão quantílica encontra-se que há uma brecha significativa a favor dos meninos, que se incrementa ao longo da distribuição. A decomposição de Juhn-Murphy-Pierce, mostra que as características pessoais, familiares e escolares explicam uma porção pequena das brechas, enquanto que diferenças nos retornos jogam um papel importante. Adicionalmente, se mostra que a brecha observada difere significativamente de acordo à região; sugerindo que características específicas de cada região como por exemplo diferenças na cultura relacionadas com o rol da mulher podem estar influenciando o desempenho das meninas.
Classificação JEL: A14, A21, C21
Palavras-chave: brecha de gênero, exames de saída, decomposição Juhn-Murphy-Pierce.
Introduction
In 2005, and in keeping with the United Nations Millennium Goals, Colombia determined to eliminate gender inequality at every level of instruction by December 2015 (PNUD, 2005). Colombia has achieved this objective for educational coverage in primary and secondary school (Delgado, 2014), but whether this goal has been achieved in terms of girls’ versus boys’ performance in the eleventh grade (i.e., before university-level education) remains in question. Thus, the equality of access to opportunities for higher education in Colombia also remains in question.
Gender inequalities in academic performance have important consequences for women´s careers and their role in society. When women lack skills and knowledge in math and reading, they have lesser opportunities to attend college in areas such as science, technology, engineering, and math (STEM). Thus, women are likely to have fewer opportunities in the future and earn lower incomes when compared to men with similar characteristics (Schrøter & Nielsen, 2013). The under-representation of women in STEM fields is in turn correlated with shortfalls in innovation, creativity, and competitiveness in business, limitations on their empowerment and leadership, limited access to positions of power, and reductions in the possibility of higher returns (Schrøter & Nielsen, 2013; Castillo et al., 2014; Morales & Sifontes, 2014). Moreover, lower educational achievement of girls for reasons other than personal capacity can, in general, cause negative cycles because girls perform worse in societies that are less egalitarian in terms of gender (Baker & Jones, 1993; Guiso et al., 2008; Monte et al., 2008; Gonzales & De la Rica, 2012). This inequality may also lead to economic losses to modern societies (Pollitzer & Schrauder, 2015).
Colombia is perceived to have high gender inequality compared to other developed and developing countries. According to the Global Gender Gap Index 2014, Colombia scored 53rd among the 144 countries analyzed. Moreover, despite the evident gender gap on the labor market and in salaries (Hoyos et al., 1994; Abadía & De la Rica, 2011), little attention has been paid to the disparities that precede these inequalities, such as the educational gap. This research hopes to contribute to the understanding of the observed and adjusted academic gender gap – where the observed gap refers to the calculation of girls’ scores minus boys’ scores, while the adjusted gap also considers this difference, but is controlled for individual, family, school, and regional factors. Using the database of the Saber 11 exams, this research aims to address the following questions: How does the observed and adjusted gender gap change along the score distribution? In what Colombian regions is the observed gap greatest? What proportion of the adjusted gap is explained by differences in students’ personal, family and school characteristics?
The rest of this paper is organized as follows: Section 2 reviews the relevant literature for the development of this research document. Section 3 describes the Saber 11 database. Section 4 presents the descriptive statistics. Section 5 describes the methodologies used to measure and decompose the gap, and section 6 presents the results. Section 7 is a conclusion.
1. Literature Review
The literature regarding the existence of gender-based gaps in school performance, their causes, and their relation to the well-being of societies is diverse. There are two main schools of thought that explain why girls tend to obtain lower scores than boys in math and higher scores than boys in reading. One school of thought suggests that the difference in performance between genders is rooted in biology. Works such as those by Lawton and Hatcher (2005), Temple and Cornish (1993), (2002), Halpern (2004), Kucian et al. (2005), and Gallagher and Kaufman (2005), for example, suggest that these differences exist because males and females differ in terms of their visual-spatial abilities, cognitive patterns, and brain functioning. These theories do not fully explain gender differences, however, and they do not account for the absence of gender gaps in some countries and cultures.
The second school of thought has been developed mainly within sociology and economics. This literature theorizes that gender gaps stem from differences in students’ social or cultural characteristics. Authors such as Baker and Jones (1993), Riegle-Crumb (2005), Guiso et al. (2008), Hyde and Mertz (2009), Fryer and Levitt (2004), and Gonzáles et al. (2012) claim that the performance of girls versus boys on school tests predicts better opportunities for women in more egalitarian societies. In less egalitarian societies, girls do not find it useful to put effort into achieving success in some areas of study because they do not expect to be able to participate in related work or public activities. These findings suggest that contextual factors in addition to biological aspects contribute significantly to the reasons for academic gender gaps.
Because geographical regions are subject to different cultural factors, estimating the academic gender gap in different countries has received special attention in the literature. Guiso et al. (2008) reported that the gender gap on the math portion of the Program for International Student Assessment (PISA) testing instrument does not show up in countries with greater gender equality as measured by women´s emancipation, rates of activity, and political empowerment. Also using PISA data, Gonzáles et al. (2012) found that differences in the cultural and social rules among different regions of Spain are crucial determinants of gender-based test differences in test results. They found that girls perform better in math and reading in those regions where gender equality is encouraged, thus suggesting that cultural aspects are at least correlated with girls’ performance.
Similarly, the work of Dickerson et al. (2015) suggests that sociodemographic aspects of different geographical areas can affect the gender gap in school performance. The authors studied 19 countries in Africa and determined that boys scored higher in math on standardized tests to a significantly variable extent in different regions. The gender gap was greater in regions with a higher proportion of women with low education, higher fertility rates, and larger populations of practicing Muslims. The adjusted gap decreased significantly when taking these characteristics into account. They concluded that regional differences are more predictive of gender gaps than other characteristics such as parents’ education or other variables such as school type.
Some studies have focused on math tests to examine the size of the gap in relation to test score distributions. The results are mixed for the lower tail of the distribution but consistent for the upper tail of the distribution. The observed gap in math is greater in the upper tail of the distribution than in the average range (Hedges & Nowell, 1995; Guimares & Sampaio, 2008). In addition, other studies (Xie & Shauman, 2003; Penner & Paret, 2008; Ellison & Swanson, 2010) have found that, at least in the United States, there is a notable underrepresentation of girls in higher distribution percentiles, and girls with exceptional performance tend to attend elite schools.
In Colombia, two studies have assessed the gender gap in academic performance. Icfes (2013) performed a descriptive analysis of the average observed gap on national tests (Saber 3, 5, 9, and 11) and international tests (Trends in International Mathematics and Science Study, hereafter TIMSS and PISA), and found that some motivational, cognitive, attitudinal, and school factors could be correlated to performance. In tests for all the different grades, girls consistently exhibit a disadvantage relative to boys in math, and in high school the difference is greater. Abadía (2017) estimated the academic gender gap of Colombian students using the PISA test, finding that the gap favored boys in math and girls in reading after adjusting for personal, family, and school characteristics. However, these two papers provide only estimates for the mean of the distribution.
This paper augments the literature in several aspects. First, we contribute to the search for new and better methods to estimate the academic gender gap across the score distribution in a Latin American context. Second, unlike previous efforts to measure the relationship between the academic gender gap and its determinants, we quantify the gap using the Juhn, Murphy, and Pierce method to decompose the gap along the score distribution and determine the extent to which it is explained by personal, family, and school characteristics. Third, we use reliable data from almost the entire population of high school students in 2014, all of whom took the same exam on the same day. This provides reliable and generalizable estimates. Finally, this is the first study in Colombia to measure the academic gender gap using the state exit exam (Saber 11) and to perform a regional analysis.
2. Data
The Saber 11 test is a mandatory instrument designed to measure students’ competencies in five subject areas. It is administered two months before students graduate from high school and it is used as a selection mechanism for higher education admissions and scholarships. We used cross-sectional data from the Saber test administered in 2014 by the Colombian Institute for the Promotion of Higher Education (Icfes). In addition to the scores, the database contains information about the socioeconomic characteristics of all students and their family, school, and regional characteristics. Unlike other tests such as PISA and TIMMS, Saber 11 is administrated to the entire population of high school students. It contains regional information and is arguably more valued by students than the other tests, given its importance for gaining access to higher education. Other important studies such as Angrist et al. (2004), have also used data from the Colombian exit exam in their research.
The Saber 11 test covers five areas: math, critical reading, social studies, natural sciences, and English as a foreign language. A global score is calculated on the basis of the individual test scores, although foreign language is given lesser weight. The scores for each of the five areas follow a scale from 0 to 100, with an average of 50 and a standard deviation of 10. The global score ranges from 0 to 500, with an average of 250 and a standard deviation of 50.
The original dataset comprises information on approximately 541,874 students. In order to analyze a more homogeneous sample, however, 35,581 students were excluded, comprising those under the age of 14 and those over the age of 21 Additionally, 923 other students with particular characteristics (usually related to issues of impairment), were excluded, as were 1,285 students who did not report any information for the variables of interest. The final sample was restricted to 504,085 students (93 % of the original observations), unevenly distributed within the 32 regions and Bogotá, the national capital.
This research used four scores as dependent variables in estimating the gap: the global score and the scores in math, sciences, and critical reading. The global score was used because it is the main criterion used by universities and other organizations for access to degree programs and scholarships such as Ser Pilo Paga, which granted scholarships to 10,000 students in 2014. Students with global scores over 310 were selected. Math, sciences, and critical reading were used because they are typically the areas of interest in the literature and are thought to represent the important skills students must have in order to succeed in various professional careers.
3. Descriptive Statistics
Table S1 presents the descriptive statistics of all variables used in estimating the gap, taken together and separated by gender. Column 1 shows that the mean of the global score was 252, and the standard deviation was 42, whereas the means of the math, science, and reading scores were approximately 50.6, and standard deviations were approximately 10. The average of the scores was slightly above the Icfes’ standardized parameters (250 points for the global score and 50 points for the areas) because the scores of the people left out of the sample were slightly lower than the rest.
Colombian students in the eleventh grade generally live in unfavorable socioeconomic conditions and are concentrated in certain regions of the country. 1 Column 1 of table S1 shows that most students have few economic resources (41 % and 35 % belong to social strata 1 and 2, respectively), 2 their parents have limited educational achievement (53 % of parents and 50 % of mothers completed elementary school or less), they study in public schools (75 %), and go to morning school (53 %) or all-day school (20 %). In addition, most students live in urban areas (80 %) in regions such as Cundinamarca (24 %), Antioquia (13 %), Valle del Cauca (7.5 %) and Atlántico (5.3 %).
Approximately half the students’ mothers do not work outside the home (52 %), whereas almost all the fathers have an occupation outside the home (96 %). The average age of the students is 16.8 years, and only 2 % report having repeated a school year. Moreover, the test takers were disproportionately female (54.5 %; 274,685 girls versus 229,400 boys). This disproportion will be significant as we further analyze the proportion of girls versus boys in the upper tail of the distribution.

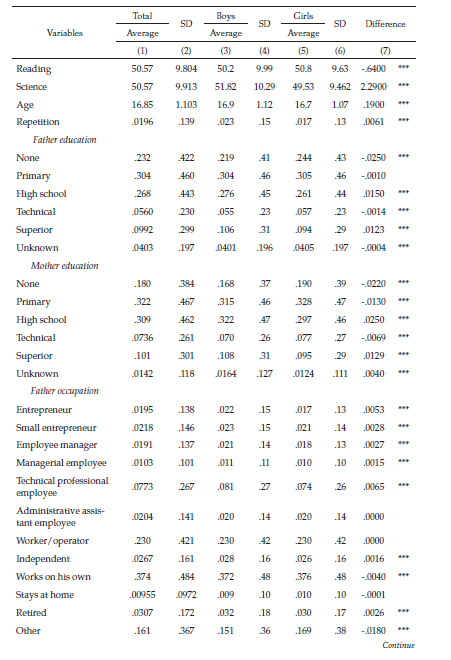
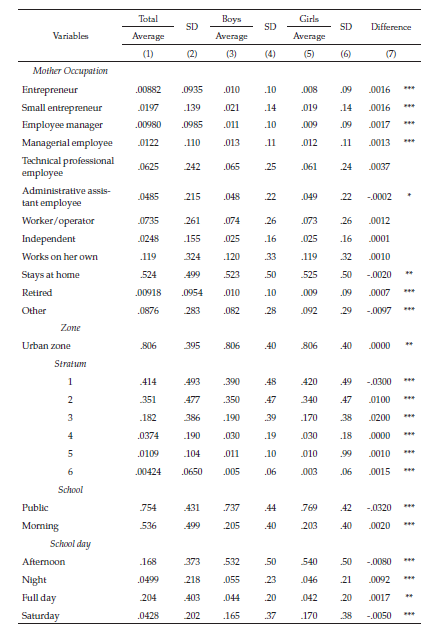
Columns 3 and 5 of table S1 show the statistics for the variables, classified by gender. The three scores report differences between boys and girls (column 7). For the math, science, and global scores, the average observed gap favors boys by 2.2, 2.3, and 5.8 points, respectively (equivalent to .22, .23 and .12 of a standard deviation). In reading, the gap favors girls, but only by .64 points (.064 standard deviation). All differences are statistically significant (column 7).
The gender-based differences in most family, school, and regional variables are subtle yet significant. In general, however, more girls than boys are exposed to more variables that are unfavorable to academic performance. In particular, a higher proportion of girls (3 %) report being in the lowest socioeconomic stratum (1), whereas a higher proportion of boys than girls report belonging to the rest of the strata. On average, a higher percentage of girls have fathers and mothers with zero years of education (24.4 % and 19 %, respectively) compared to boys (21.9 % and 16.8 %), and a lower percentage of girls have fathers and mothers with higher education (9.4 % and 9.5 %, respectively) compared to boys (10.6 % and 10.8 %). Likewise, girls have a higher probability of being enrolled in public schools, where performances tend to be lower, than in private schools, where performances tend to be higher. Regarding the regional distribution, the proportions between girls and boys are relatively close to the average.
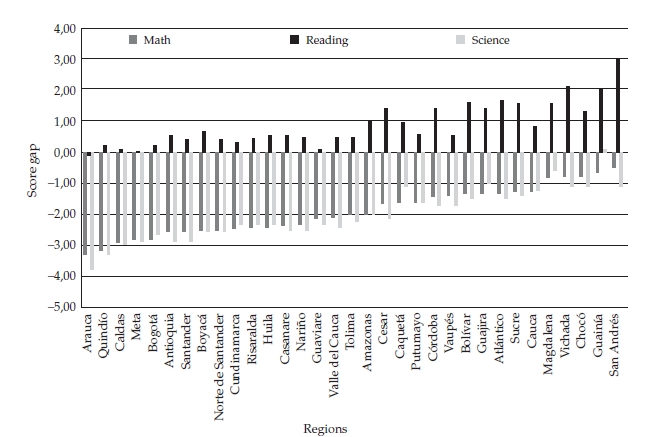
The observed gaps for different regions are heterogeneous, and the magnitude of the gap varies by region. In Arauca, for example, the gaps in math and science are -3.2 and -3.8 points, respectively, whereas in San Andrés, they are only -.5 and -1.1. Likewise, the gap in reading tends towards zero in Arauca but is 3 in San Andrés. The correlation between the observed gaps in math and reading by region is approximately .88. This means that regions with greater math gaps disfavoring girls have smaller disparities favoring girls in reading, and vice versa. The correlation and interpretation of the relation between science and reading is also equivalent. These results are consistent with the literature (Guiso et al., 2008).
Figure 2 shows the gap in global scores for the 32 regions and Bogotá. Among them, 22 regions exhibit negative and statistically significant gaps. Arauca, Quindío, Caldas, Meta, and Bogotá have the largest observed gaps disfavoring girls in math and science, and the smallest gaps or no difference at all in favor of girls in reading. The heterogeneity of the gap among regions with similar distributions of boys and girls permits the hypothesis that social, cultural, and/or regional aspects may be related to girls’ performance. Nonetheless, this revealing correlation must be further analyzed in additional studies to support the hypothesis.
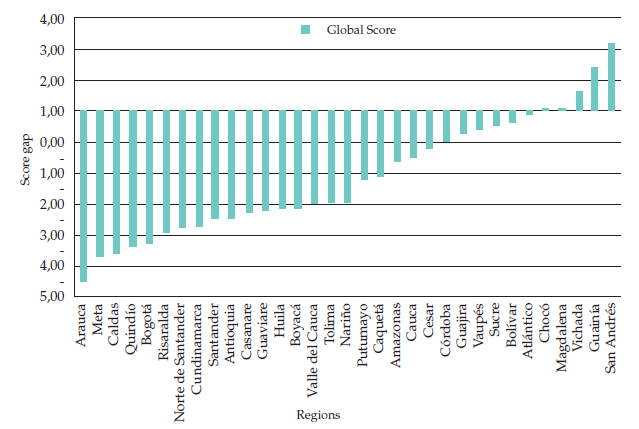
Figure3 shows the kernels of the distributions for the global, math, science, andreading scores of boys and girls. The score distribution for girls is lowerthan that for boys at the middle and upper parts of the distribution of global,science, and math scores, suggesting that the gender score gap widens as thesescores increase. We performed a Wald test and found that these gaps weresignificantly different from zero in all cases.

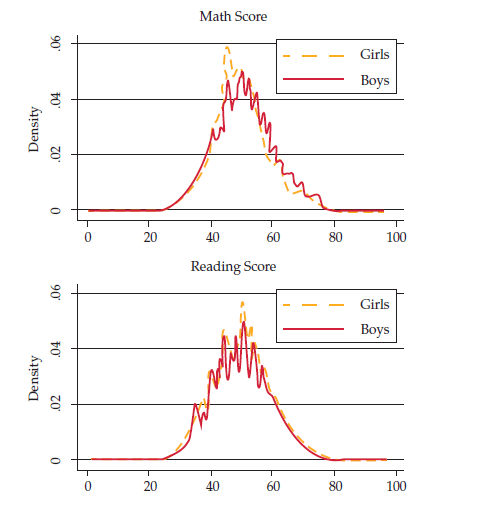
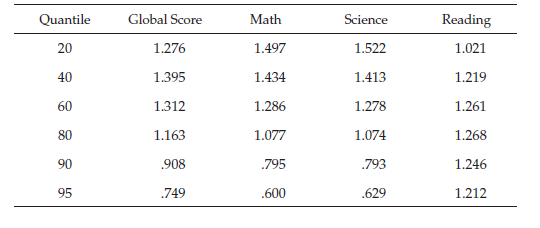
Additionally, the girl-to-boy ratio alongthe distribution is uneven. Table S2 reports the boy-to-girl ratios for eachquantile of the distribution. The proportion for the complete sample is 1.2(274,685 girls versus 229,400 boys). If boys and girls were equally distributedamong the scores, this proportion could be expected to replicate in allquantiles of the distribution. However, girls are underrepresented in the uppertail of the math, science, and global score distributions. In quantile 95, theproportions are .75, .60 and .63, respectively. In other words, the number ofgirls eligible for admission to highly ranked universities or for governmentscholarships is disproportionately lower than the number of eligible boys, eventhough there are more girls in the educational system.
4. Methodology
We calculate the adjusted gender gap in school performance (the gap between girls and boys is similar in terms of observed characteristics) at the mean and by quantiles using ordinary least squares (OLS) and quantile regression (QR). Both methodologies are supported based on the Education Production Function proposed by Hanushek (1979), where the inputs are student attributes, family characteristics, and school resources, and the output is student performance.
Equation 1 represents the function to be estimated by OLS.
where Y i is the student score (global score, math, science, or reading); ͞Pι+ ͞Fι+ ͞Sι are vectors of the personal, family, and school characteristics for each student; G is a dummy that equals 1 if the student i is a girl and 0 if the student is a boy; and εi corresponds to an error term that gathers random disturbances. Thus, the main parameter of interest for this research is ß1. If is negative ß1, there is a gap that disadvantages girls.
Moreover, QR (Koenker & Basset, 1978) allows for estimating the impact of gender on scores at different points of the conditional distribution. The model to be estimated may be represented as follows:
where q is anumber between zero and one and Qq (Yi |Gi ,͞P 1, ͞F 1, ͞S 1) isthe quantile of the conditional score to the set of regressors of the student .The quantile estimator ˆβq is minimized in the following targetfunction:
In this manner, if q = .90, for example, the function gives greater importance to the prediction of observations y < x' ß than to the observations .
Additionally, the Juhn et al. (1993) methodology is used to decompose the observed gender gap in school performance, applicable to differences in the distribution of observable characteristics (quantities effect), the distribution of returns of the described characteristics (price effect) and changes in the distribution of the residuals (quantities and price effects of unobservable skills).
The distribution of scores may be expressed as follows:
where G = m,f indicates boys and girls, respectively; X i a vector of observed characteristics; and the last term of the equation (4), ε i G = F G-1 (θi G | Xi G) is the inverse of the accumulated residual function, which is composed of two parts: the quantile of an individual i in the residuals distribution of θi G and the residuals distribution function, Fi .
The difference in the scores of boys and girls in a determined quantile (Ym -Yf ) may be decomposed as follows:
where equations (5), (6), and (7) represent the differences in the distribution of observable characteristics (quantities effect), the differences in the distribution of the returns of those characteristics (price effect), and the changes in the residual distribution (residuals effect), respectively.
These methodologies are expected to capture the magnitude of the gender gap and its relationship with different student characteristics. The measurements may be far from causal, because variables that bias the coefficients in some way may be omitted. Nevertheless, this methodology can help us identify how much of the gap could be a response to important aspects such as parents’ education, socioeconomic strata, or meeting time at school, and how much of the gap is not related to those aspects. This helps us identify aspects that could be driving the gap. This bias might be counteracted with the use of a longitudinal database, but none was available at the time of this study.
5. Results
Adjusted gender gap
The results of the estimate of the adjusted gender gap in relation to test scores are presented in table S3. The first column shows the estimated gap in the mean (OLS estimate), whereas the rest of the columns in each table show the estimated gap in quantiles 20, 40, 60, 80, and 95 (quantile regression).
The dependent variable is the score (global, math, science, and reading), and the variable of interest is the coefficient of the gender dummy. In addition, all estimates include the following as controls: i. personal variables such as gender, age, age squared, and a dummy that indicates if the student has taken the test more than once; ii. family variables such as parents’ education level and occupation, socioeconomic stratum, and region; and iii. school variables such as hours of school attendance, where the school is located, and whether the school is public or private.
The results of the estimate reveal that girls’ math, and science, and global scores are lower than those of boys with similar observable characteristics. Moreover, we confirm that girls obtain higher scores in reading, but the differences are small.
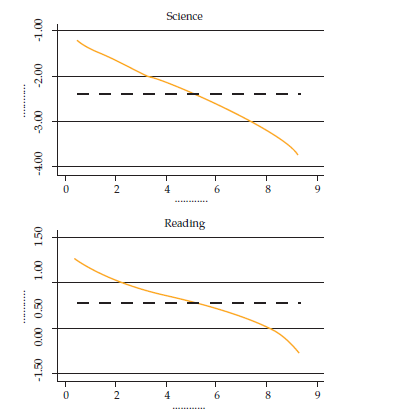
Figure4 illustrates the behavior of the adjusted gap along the score distributions. 3

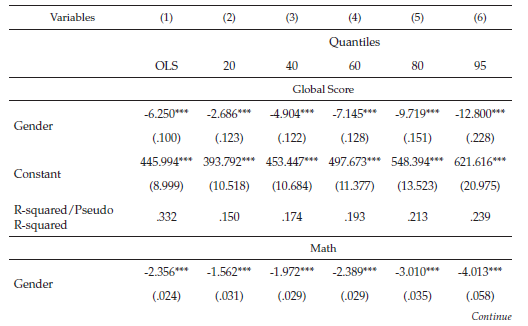
The first panel of table S3 shows the estimated gap in the global score. Gender-based differentials are negative and statistically significant on average in the five analyzed quantiles. This result indicates that girls do not perform as well as boys with similar characteristics along the distribution. On average, the magnitude of the gap reaches -6.25 points (.15 of a standard deviation) to the detriment of girls, which is slightly higher than the average observed gap of -5.8 points (.14 of a standard deviation).
This gap increases steadily along the global score distribution, emphasizing the gender differential on the upper tail of the distribution. At the low end of the distribution (in the lowest 20 % of scores), the gap has a magnitude of -2.7 points (.05 of a standard deviation), whereas the gender difference is almost -13 points (.26 of a standard deviation) among the highest 5 % of scores.
The results regarding the estimated gap in math and science are similar to those of the global score, although of smaller magnitude. In the case of math, the gender dummy is negative and statistically significant. On average, the difference is approximately -2.4 points (.23 of a standard deviation) to the detriment of girls. However, the gap increases as the scores increase. In quantile 20, the gender difference in the math score is -1.6 points (.16 of a standard deviation), and it increases to a -4 point difference (.4 of a standard deviation) in quantile 95 (Figure 4).
In science, the average adjusted score gap is -2.4 points (.24 standard deviation) to the detriment of girls, and it increases with higher scores. The first quantile analyzed exhibits a gap of -1.7 points (.17 of a standard deviation), and the last quantile reaches a gap of -3.7 (.37 of a standard deviation).
Finally, the last panel of table S3 shows the estimated gender gap in the reading score. The results confirm that girls have a slight advantage in reading. The gender dummy is positive and statistically significant along the score distribution, except for quantile 95, where girls scored approximately .6 of a point (.06 of a standard deviation) higher than boys. The gap is smaller at the lower end of the distribution than at the higher end. In quantile 20, the difference is .9 points (.09 of a standard deviation), and it steadily decreases and becomes negative (-.127 points and .013 of a standard deviation) when comparing the students who obtained the highest 5 % of scores. 4 The gender gap in reading throughout the score distribution is the only one that favors girls in almost the entire distribution.

Theresults obtained are consistent with the findings of previous studies aroundthe world researching international standardized tests such as PISA and TIMSS, which concludethat boys outperform girls in math and science, but underperform them inreading (Guiso et al., 2008; Marks, 2008; Gonzales & De la Rica, 2012;Dickerson et al., 2015).
JMP decomposition
The previous section confirmed the existence of consistently gendered score gaps, even when controlling for observable attributes of students. However, we are still unable to identify how these observable factors contribute to explaining the differences in girls’ and boys’ academic performance. Thus, we use JMP decomposition to quantify the extent to which observable and non-observable factors contribute to explaining gender gaps (table S4) and to determine the extent to which personal, family, and school characteristics explain the quantities effect (table S5).
Table S4 shows that the average gap in the global score is approximately -5.8 points (.12 of a standard deviation). The component “Quantity Effect” is negative, although small. Thus, it can be said that if girls had same set of observable characteristics as boys, the gap would be slightly higher in all quantiles except for some upper ones (quantiles 90 and 95), where boys are advantaged. Observed personal and school characteristics favor girls, but family factors counteract most of the effect. The impact of personal characteristics on scores is similar through the quantiles whereas school factors favor girls except in the highest quantiles. The greatest part of the gap is explained by differences in the returns of observed characteristics (price effect), which favor boys. The magnitude of these differences increases with the scores. When girls had the same returns as boys, the gap was lower; it would disappear on average and would be reduced by half in the highest quantile. Moreover, the differences in residuals (the component of non-observable variables) play almost no role in the explanation of the gap on average. They do, however, explain almost 50 % of the gap on the right tail of the score distribution.
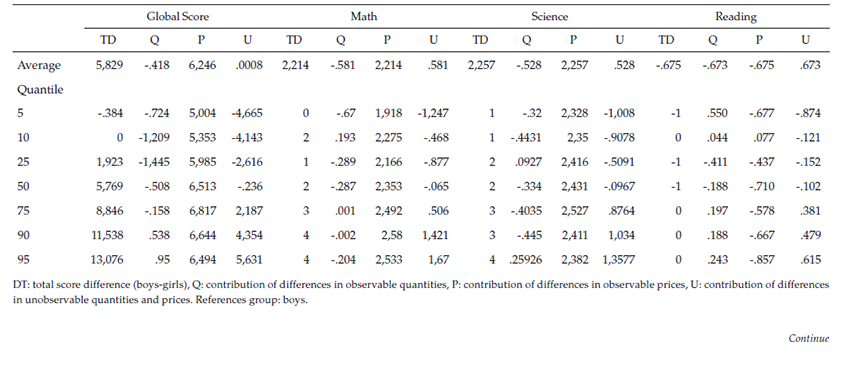
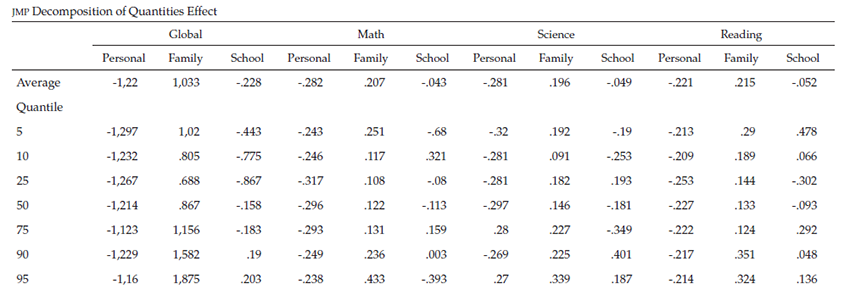
The results of JMP decomposition in the math and science scores are similar to those of the global score. The observed gap favors boys on average and in all quantiles, except in quantile 5 for math. Observable personal and school factors favor girls, but family factors do not. The set of family characteristics almost fully counteracts the effect of observable personal and school factors at the mean. In addition, family characteristics have a greater magnitude compared to other factors at the high point of the distribution. Again, the greatest part of the gap is explained by boys’ higher returns for the observable characteristics (price effect), increasing at the right end of the distribution. In the 95th quantile, this component explains 63 % and 60 % of the gap in math and science, respectively. That is, the production function of education is more pronounced for male students than for female students, especially those with higher scores. Likewise, differences in the non-observables (residuals effect) are positively correlated with the gap observed in higher scores.
Finally, the results of the JMP estimate for reading differ from those observed in the other areas. As mentioned above, the gendered gap in reading scores favors girls, but it is small (on average .675 points, .068 of a standard deviation), and the advantage for girls only appears at the lowest scores. On average, differences in observable personal and school factors and in the returns of the whole set of characteristics favor girls, whereas residuals do not greatly help to explain the gender gap. However, the effects are mixed throughout the score distribution. On the lower tail of the distribution, returns and residuals favor girls but observable characteristics do not. On the right tail of the distribution, on the other hand, the effect of returns is stronger and still favors girls, but the effect of residuals is opposite to that observed at lower scores, reversing the gap and favoring boys.
6. Discussion and Conclusions
There are significant gender differences in school performance in Colombia. Boys score better on standardized global, math, and science tests, as do girls on reading tests. Using information derived from the national test known as Saber 11, the results of this study reveal that after adjusting for observable personal, family, and school characteristics, there are persistent academic gaps between boys and girls. There is a statistically significant gap that favors boys’ global, math, and science scores, which is accentuated among students with higher scores. Girls score slightly higher than boys in reading, but the difference is reduced along the distribution and actually favors boys in the uppermost quantile. The widening of the gaps along the distribution and the underrepresentation of girls among outstanding scores aggravate girls’ unfavorable performance compared to boys.
A performance analysis by gender among regions finds that gaps differ significantly among the different regions of Colombia. Girls have lower global scores in every region analyzed, and Arauca, Quindío, Caldas, Meta, and Bogotá are the 5 regions with the largest gaps. Likewise, in regions where girls have less advantages in reading compared with boys, girls also have greater disadvantages in math and science. This evidence favors the arguments that highlight social, cultural, and regional determinants over biological factors in determining gender differences in performance (Guiso et al., 2008).
We also find that a small part of the gap is explained by the differences in personal, family, and school characteristics. Using JMP methodology, we rule out observable factors that are determinants of overall performance as determinants of the gender gap. To a great extent, the gap is attributed to unobserved factors, which become more significant on the upper tail of the distribution. This finding suggests that broader factors such as attitudes (Tinklin, 2003), academic environment (Zimmerman, 2003), and differences in the roles played by men and women in Colombian society could contribute to explaining some part of the gap. Future research might explore this hypothesis.
Due to the non-experimental nature of the study, it is not possible to infer causal relationships between the determinants of the gap. That being said, we believe that our study presents solid evidence of the existence of an achievement gap between boys and girls, that based on the current literature, represents a problem with undesirable consequences for society. This is especially so because the underperformance of girls contributes to the perpetuation of social inequality. The lower academic performance of girls as measured by the national test Saber 11 and in subjects such as science and math predicts that a significant number of girls will continue having restricted access to higher education, and particularly to STEM careers.
Girls’ underperformance reduces their access to available opportunities for higher education. For example, women were underrepresented in the national scholarship program Ser Pilo Paga, which in 2015 awarded 10,141 students with access to higher education. Although 54 % of students taking the qualifying exam were female, only 43 % of females were eligible for the scholarship. By way of a counterfactual exercise, if there had not been a gender gap, around 4,000 more females would have been eligible for Ser Pilo Paga scholarships.
Moreover, in 2015 almost the same percentage of women and men enrolled in their first semester of higher education (49.6 % female). However, only 32 % of female students enrolled in STEM programs. These programs demand a higher Saber 11 score in areas such as math and science, where females underperform males. Correspondingly, the underrepresentation of women in STEM activities implies a continued waste of available intellectual resources and a lost opportunity for society (Pollitzer & Schrauder, 2015).
This study highlights the need to identify effective policies to promote the performance of girls, particularly in math and science, which may incrementally increase the representation of women among scientists and engineers, thus boosting research and innovation and therefore economic growth (OECD, 2011). Particularly, awareness campaigns can be conducted to lessen gender stereotypes in homes and schools (such as “math is just for boys” or “boys should think about engineering and girls about the kitchen”), by promoting talks that involve female role models in important positions in society and in STEM fields. Combating sexism and gender stereotyping would help motivate girls work harder and improve their academic results. Laws and policies to eliminate sexism from the classroom were passed several years ago in some developed countries such as the U.S.A. and Canada (Coulter, 1996; Ramsey, 1998), but this topic is rarely discussed in Colombia and some other Latin American countries.
Independent of the specific strategies that are embraced to address these issues, this research suggests that any steps taken to address the academic gender gap must be adjusted to the context in which girls live, and must go beyond the typical reinforcement in the areas in which girls are disadvantaged. Given the size of the gaps found along the distribution and in the regions, interventions must be differentiated according to the sociocultural characteristics of the regions in which girls grow up, and to low, medium, and high student performance. In other words, a strategy for average girls in a particular region cannot be expected to work for high-performing girls in other regions, or even in the same region. Likewise, given the high correlations between math, science, and reading, specific reinforcement in math will most likely help improve the results in areas not directly targeted, such as reading or science. Improved practices along these lines can provide girls with greater access to the best opportunities for higher education and hopefully help us move toward a more equitable society.
References
Abadía, L. (2017). Gender score gaps of Colombia in PISA test. Vniversitas Económicas, 17(8), 1-24.
Abadía, L., & De la Rica, S. (2011). Changes in the gender wage gap and the role of education and other job characteristics Colombia: 1994- 2010. Vniversitas Económicas, 11(8), x-x.
Angrist, J., Bettinger, E., & Kremer, M. (2004). Long-term consequences of secondary school vouchers: Evidence from administrative records in Colombia. National Bureau of Economic Research, w10713.
Baker, D. P., & Jones, D. P. (1993). Creating gender equality: Cross-national gender stratification and mathematical performance. Sociology of Education, 66(2), 91-103.
Castillo, R. Grazzi, M., & Tacsir, E. (2014). Women in sience and technology. Ciudad: Interamerican Development Bank. Recuperado de https://publications.iadb.org/bitstream/handle/11319/6047/CTI%20TN%20Women%20in%20Science%20and%20Technology.pdf?sequence=1
Coulter, R. P. (1996). Gender equity and schooling: Linking research and policy. Canadian Journal of Education/Revue, 21(4), 433-452.
Delgado, M. (2014). La educación básica y media en Colombia: retos en equidad y calidad. (Fedesarrollo). Recuperado de http://www.fedesarrollo.org.co/wp-content/uploads/2011/08/La-educaci%C3%B3n-b%C3%A1sica-ymedia-en-Colombia-retos-en-equidad-y-calidad-KAS.pdf
Dickerson, A., McIntosh, S., & Valente, C. (2015). Do the maths: an analysis of the gender gap in mathematics in Africa. Economics of Education Review, 46, 1-22.
Ellison, G., & Swanson, A (2010). The gender gap in secondary school mathematics at high achievement levels: evidence from the American mathematics competitions. Journal of Economic Perspectives, 24(2), 109-128.
Fryer Jr, R.G., & Levitt, S. D. (2004). Understanding the black-white test score gap in the first two years of school. Review of Economics and Statistics, 86(2), 447-464.
Gallagher, A. M., & Kaufman, J.C. (2005). Gender differences in mathematics: an integrative psychological approach. Cambridge: Cambridge University Press.
Gallagher, A., Levin, J., & Cahalan, C. (2002). Cognitive patterns of gender differences on mathematics admissions tests. ETS Research Report Series, 2, 1-30.
Gonzales, A., & De la Rica, S. (2012). Gender gaps in pisa test scores: the impact of social norms and the mother’s transmission of role attitudes. IZA DP No. 6338. Recuperado de http://ftp.iza.org/dp6338.pdf
Guimarães, J. C., & Sampaio, B. (2008). Mind the gap: evidences from gender differences in scores in Brazil. Niteroi, Rio de Janeiro: ANPEC - Associação Nacional dos Centros de Pósgraduação em Economia [Brazilian Association of Graduate Programs in Economics].
Guiso, L., Monte, F., Sapienza, P., & Zingales, L. (2008). Culture, gender, and math. Science, 320(5880), 1164-1165.
Halpern, D. F. (2004). A cognitive-process taxonomy for sex differences in cognitive abilities. Current Directions in Psychological Science, 13(4), 135-139.
Hanushek, E. A. (1979). Conceptual and empirical issues in the estimation of educational production functions. Journal of Human Resources, 14(3), 351-388.
Hedges, L. V., & Nowell, A. (1995). Sex differences in mental test scores, variability, and numbers of high-scoring individuals. Science, 269(5220), 41-45.
Hoyos, A., Ñopo, H., & Pena, X. (1994). The persistent gender earnings gap in Colombia. 1994-2006 (May 2010). IDB Working Paper No. 54.
Hyde, J. S., & Mertz, J. E. (2009). Gender, culture, and mathematics performance. Ciudad: University of Wisconsin, Department of Psychology.
Icfes (2013). Análisis de las diferencias de género en el desempeño de estudiantes colombianos en matemáticas y lenguaje. Bogotá: Icfes SABER INVESTIGAR.
Juhn, C., Murphy, K. M., & Pierce, B. (1993). Wage inequality and the rise in returns to skills. The Journal of Political Economy, 101(3), 410-442.
Koenker, R., & Bassett Jr, G. (1978). Regression quantiles. Econometrica: Journal of the Econometric Society, 6(1), 33-50.
Kucian, K., Loenneker, T., Dietrich, T., Martin, E., & Von Aster, M. (2005). Gender differences in brain activation patterns during mental rotation and number related cognitive tasks. Psychology Science, 47(1), 112-131.
Lawton, C. A., & Hatcher, D. W. (2005). Gender differences in integration of images in visuospatial memory. Sex Roles, 53(9), 717-725.
Marks, G.N. (2008). Accounting for the gender gaps in student performance in reading and mathematics: evidence from 31 countries. Oxford Review of Education, 34(1), 89-109.
Morales, R., & Sifontes, D. (2014). Desigualdad de género en ciencia y tecnología: Un estudio para América Latina. Observatorio Laboral Revista Venezolana, 7(13), 95-110.
Organization for Economic Cooperation and Development (OECD). (2011). Report on the gender initiative: Gender equality in education, employment and entrepreneurism. Paris: OECD publishing. Recuperado de http://www.oecd.org/social/48111145.pdf
Penner, A. M., & Paret, M. (2008). Gender differences in mathematics achievement: Exploring the early grades and the extremes. Social Science Research, 37(1), 239-253.
PNUD (2005). Hacia una Colombia equitativa e incluyente. Informe de Colombia. Objetivos de desarrollo del milenio. Bogotá: DNP.
Pollitzer, E., & Schraudner, M. (2015). Integrating gender dynamics into innovation ecosystems. Sociology and Anthropology, 3(11), 617-626.
Ramsey, C. B. (1998). Subtracting sexism from the classroom: Law and policy in the debate over all-female math and science classes in public schools. Texas Journal of Women & the Law, 8(1), 1.
Riegle-Crumb, C. (2005). The cross-national context of the gender gap in math and science. In L. V. Hedges & B. Schneider (Eds.) The social organization of schooling (pp. 227-243). New York: Russell Sage Foundation.
Schrøter, J. J., & Nielsen, H. S. (2013). Math and gender: Is math a route to a high-powered career? IZA DP No. 7164. Recuperado de http://ftp.iza.org/dp7164.pdf
Temple, C. M., & Cornish, K. M. (1993). Recognition memory for words and faces in schoolchildren: A female advantage for words. British Journal of Developmental Psychology, 11(4), 421-426.
Tinklin, T. (2003). Gender Differences and High Attainment. British Educational Research Journal, 29(3), 307-325. Recuperado de http://www.jstor.org/stable/1502255
Xie, Y., & Shauman, K.A. (2003). Women in science: Career processes and outcomes. Boston, MA: Harvard University Press.
Zimmerman, D. J. (2003). Peer effects in academic outcomes: Evidence from a natural experiment. Review of Economics and Statistics, 85(1), 9-23.
Notes
*
This research received the support of the Instituto colombiano para la evaluación de la educación (Icfes) and the Pontificia Universidad Javeriana (PUJ). The project was designated Brechas de Género en el Rendimiento Escolar a lo Largo de la Distribución de Puntajes: Evidencia Pruebas Saber 11.°, IDPPTA 6377. The opinions, thesis and arguments expressed are the authors’ and do not represent these institutes’ points of view. The authors especially thank Juan Manuel García Ospina for his cooperation as a research assistant.
1
This sample includes a total of 32 regions plus the capital, Bogotá.
2
A socio-economic stratification system in Colombia classifies urban housing into different strata based on its economic characteristics. The system classifies urban areas on a scale from 1 to 6, with 1 being assigned to areas where the poorest people live and 6 to areas where the wealthiest people live.
3
The Wald test allows for a rejection of the null hypothesis, which means that the estimated coefficients of the gender dummy are statistically different at a significance level of 99 % in each estimate.
4
As a robustness check of our result, we conducted similar analyses using 2009 and 2012 Saber 11 cohorts. Even though for years before 2014, the Saber 11 database had a different structure, the estimates of the gap and control variables hold. Results are available upon request.
Author notes
† Correspondencia: Carrera 7 # 40B-98, Edificio Jorge Hoyos, Pontificia Universidad Javeriana, Bogotá, Colombia. Tel. 320 8320, Ext.5125.



