
ISSN:0123-5362 | eISSN:2145-454X



La estructura a plazos del riesgo interbancario*
Term Structure of Interbank Risk
A estrutura a prazos do risco interbancário
Guillermo Andrés Cangrejo Jiménez
La estructura a plazos del riesgo interbancario*
Revista de Economía del Rosario, vol. 19, no. 2, 2016
Universidad del Rosario
Guillermo Andrés Cangrejo Jiménez guillocangrejo@hotmail.com
Acciones & Valores S.A., Colombia
Recepción: 15 Agosto 2014
Aprobación: 24 Septiembre 2016
Resumen:
Este documento propone un modelo para la estructura a plazos del riesgo interbancario a partir del spread entre los Interest Rate Swap (IRS) y los Overnight Indexed Swaps (OIS) en dólares durante la crisis financiera 2007-2008 y la crisis del euro en 2010. Adicionalmente, hace la descomposición del riesgo interbancario entre riesgo de default y no-default (liquidez). Los resultados sugieren que la crisis financiera tuvo importantes repercusiones en la estructura a plazos del riesgo interbancario y sus componentes: en los años previos a la crisis, el riesgo de no-default explicaba la mayor parte del riesgo interbancario; durante la crisis y posterior a ella, el riesgo de default conducía el comportamiento del riesgo interbancario. Además, se encuentra que, a partir de la estructura a plazos de cada componente del riesgo interbancario, la crisis financiera se caracterizó por ser un problema más de corto que de largo plazo, en contraste con la crisis del euro de 2010. Estos resultados siguen lo propuesto por Filipovic y Trolle (2012) y dejan importantes implicaciones sobre el riesgo interbancario durante los periodos de stress financiero.
Clasificación JEL: C32 G24
Palabras clave riesgo interbancario, estructura a plazos, riesgo de default y de liquidez.
Abstract:
This paper proposes a model for the term structure of interbank risk measured by the spread between the Interest Rate Swaps (IRS) and the Overnight Indexed Swaps (OIS) in dollars during the 2007-2008 financial crises and the crisis of the euro in 2010. Additionally, the model makes a decomposition of interbank risk between default and non-default risk (liquidity). Results suggest that the financial crisis had a significant impact on the term structure of interbank risk and its components, years before the crisis; the non-default risk was bigger than default risk; after the crisis default risk driving the behavior of interbank risk. Additionally, the results suggest that, from the term structure of each component of interbank risk, the financial crisis was characterized as a short-term problem that, in contrast to the euro crisis 2010. These results are consistent with Filipovic y Trolle (2012) and propound significant implications on the interbank risk during periods of financial stress.
JEL Classification: C32 G24
Keywords: Interbank risk, Term structure, default risk, Kalman filter, Swaps.
Resumo:
Este documento propõe um modelo para a estrutura a prazos do risco interbancário a partir do spread entre os Interest Rate Swap (IRS) e os Overnight Indexed Swaps (OIS) em dólares durante a crise financeira 2007-2008 e crise do euro em 2010. Adicionalmente, faz a decomposição do risco interbancário entre risco de default e não-default (liquidez). Os resultados sugerem que a crise financeira teve importantes repercussões na estrutura a prazos do risco interbancário e os seus componentes: nos anos prévios à crise, o risco não-default explicava a maior parte do risco interbancário; durante a crise e posterior a ela, o risco de default conduzia o comportamento do risco interbancário. Além disso, encontra-se que, a partir da estrutura a prazos de cada componente do risco interbancário, a crise financeira de caracterizou por ser um problema mais de curto que de longo prazo, em contraste com a crise do euro de 2010. Estes resultados seguem o proposto por Filipovic e Trolle (2012) e deixam importantes implicações sobre o risco interbancário durante os períodos de stress financeiro.
Clasificación JEL: C32 G24
Palavras-chave: risco interbancário, estrutura a prazos, risco de default e de liquidez.
Introducción
El riesgo interbancario puede ser entendido como la contingencia de incurrir en pérdidas derivadas de operaciones en el mercado interbancario por diversas razones, entre ellas un evento de impago o iliquidez. Este tipo de riesgo puede ser un importante indicador de la percepción de riesgo del mercado financiero en general, debido a que se caracteriza por ser el referente para formar expectativas de tasas de fondeo/colocación en otras operaciones del mercado de capitales.
Durante la última crisis financiera de 2008, los agentes de los mercados financieros estuvieron ampliamente expuestos a este tipo de riesgo y afrontaron grandes pérdidas en operaciones interbancarias. Por un lado, el riesgo de que un banco perteneciente al mercado interbancario hiciera default aumentó considerablemente debido a la insolvencia y a las grandes pérdidas registradas en el sistema financiero en general; posteriormente, este riesgo se materializó con la quiebra de bancos como Bear Stearns, Lehman Brothers y entidades hipotecarias como Freddie Mac y Fannie Mae, entre otros agentes del mercado 1 . Por otro lado, riesgos de mercado y sistémico afectaron la exposición al riesgo de liquidez en el mercado interbancario, lo que hizo que un alto volumen de activos se liquidara a precios inferiores a los de mercado. Sin duda alguna, esta crisis dejó importantes lecciones, tanto para los agentes económicos como para los policy makers, como también evidenció grandes falencias en políticas y mediciones de este tipo de riesgos.
La Libor (London Interbank Offered Rate) es una tasa de referencia diaria de las operaciones interbancarias no aseguradas en los principales mercados monetarios. Este tipo de operaciones se caracterizan por ser, en su mayoría, overnight (cumplimiento con plazo a un día) y es publicada por el British Bankers Association. Resulta del promedio de las posturas de los costos de fondeo no asegurados de los bancos pertenecientes a un panel conocido como Libor panel.
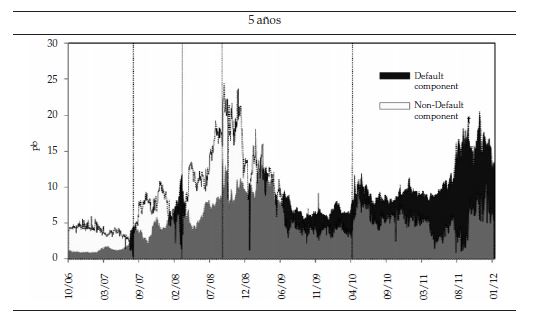
En la literatura, son muy usadas distintas medidas que recogen gran parte del comportamiento del riesgo interbancario; una medida exacta y estandarizada no es ampliamente usada debido a la complejidad de su medición. Filipovic y Trolle (2012) proponen medir el riesgo interbancario como el spread existente entre la Libor a 3 meses y los Overnight Indexed Swaps (OIS) 2 . La Libor a 3 meses es la tasa de referencia de operaciones no colateralizadas, mientras que la tasa de los OIS con vencimiento en 3 meses es una aproximación de una tasa libre de riesgo; el spread resultante (Money Market Spread) es usado como una medida aproximada del riesgo interbancario de corto plazo. Para plazos mayores a 6 meses (para los cuales la Libor no existe), la tasa de referencia de operaciones no colateralizadas son los Interes Rate Swap IRS 3 ; el spread resultante (Swap Spread) son las expectativas de mercado del riesgo interbancario para distintos plazos. Construyendo estos spreads para los plazos disponibles en el mercado, se obtiene una aproximación a la estructura a plazos del riesgo interbancario. El comportamiento de estos spreads, siguiendo lo propuesto por Filipovic y Trolle (2012), se pueden observar en la figura 1. En el panel superior se muestra el Money Market Spread junto con el Swap Spread con plazo a 1 año. En el panel inferior se muestra Money Market Spread junto con el Swap Spread con plazo a 5 años. Las líneas horizontales corresponden al inicio de la crisis financiera en agosto de 2007, la venta de Bear Stearns a J.P. Morgan en marzo de 2008, la quiebra de Lehman Brothers en septiembre de 2008 y, finalmente, la reducción de la calificación crediticia por parte de Standard and Poor’s a la deuda soberana de Grecia en abril de 2010.
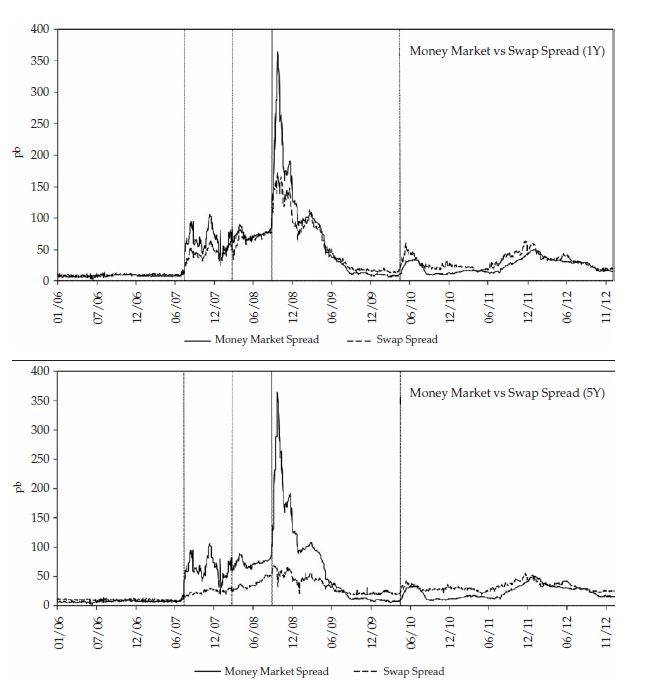
En los periodos previos a la crisis, la estructura a plazos del riesgo interbancario era relativamente plana y su magnitud rondaba los 9 y 10 puntos básicos (pb) para los plazos a uno y cinco años, respectivamente. Posteriormente, desde el inicio de la crisis financiera, en agosto de 2007 hasta la quiebra de Lehman Brothers en septiembre de 2008, el Money Market Spread aumentó considerablemente en mayor proporción que los Swap Spreads hasta estar alrededor de 11 y 50 pb por encima para los vencimientos de uno y cinco años, respectivamente. En octubre de 2008 el Money Market Spread tocó el máximo de 364 pb, mientras los Swap Spreads a 1 y 5 años alcanzaron a tocar 190 y 69 pb, respectivamente; niveles superiores a los registrados en los periodos previos a la crisis. Durante la crisis, el Money Market Spread se encontró por encima de los Swap Spread, lo que evidenció la pronunciada pendiente negativa en la estructura a plazos del riesgo interbancario. Para finales de 2009, los Swap Spreads volvieron a estar por encima del Money Market Spread, pero ambos en niveles superiores a los del periodo precrisis.
La literatura resalta que la existencia de una pendiente negativa en la estructura a plazo de este riesgo denota que los mercados tenían expectativas que existían problemas de liquidez y deterioro crediticio de las entidades bancarias en Estados Unidos, pero que dichos problemas eran más de corto que de largo plazo.
Por otro lado, Filipovic y Trolle (2012) aducen los movimientos de la estructura a plazos a dos factores principalmente: riesgo de default y riesgo de no-default. El primero de ellos, surge debido a que la Libor es construida a partir de las expectativas que tiene un banco del Libor panel de los costos de fondear/colocar los recursos, mientras que los OIS, al no depender de un panel explícito, serían análogo a una tasa Libor construida a partir de un conjunto más amplio de bancos con mejores condiciones crediticias y financieras 4 . Un banco perteneciente al panel de construcción de la Libor está expuesto a sufrir cambios en las condiciones crediticias intrínsecas propias, lo que conllevaría a que dicho banco salga del panel. Por otro lado, el riesgo de no-default está asociado, entre otras razones, con la liquidez. Dado que el Money Market Spread y los Swap Spreads son la diferencia entre una tasa con y sin colateral, dichos spreads también reflejan el costo adicional de vender un activo a un precio menor por falta de liquidez.
Otros autores han usado distintas metodologías y técnicas en el estudio de la estructura a plazos del riesgo interbancario. Inicialmente, Collin-Dufresne y Solnik (2001) obtuvieron una estructura a plazos del riesgo interbancario a partir del spread entre los bonos corporativos de los bancos en el panel de la Libor y los IRS del mercado. Estos autores concluyen que el deterioro crediticio de estos bancos es una de las causas principales de los movimientos en la estructura a plazos. Posteriormente, trabajos de Liu, Longstaff y Mandell (2006), Johannes y Sundaresan (2007) y Feldhutter y Lando (2008) calculan este spread también a partir de bonos corporativos, pero excluyen por completo el hecho del deterioro crediticio. En ambos casos, el resultado no está limpio de problemas de iliquidez en los títulos durante los periodos de crisis. Otras investigaciones como la de McAndrews, Sarkar y Wang (2008), Michaud y Upper (2008), Taylor y Williams (2009), Eisenschmidt y Tapking (2009), Schwartz (2010) y Filipovic y Trolle (2012) descomponen el riesgo interbancario entre riesgo de default y no-default. En general, las investigaciones llevadas a cabo antes de la crisis concluyen que el riesgo de no-default es el que más explica el comportamiento del riesgo interbancario, mientras que los escritos después de la crisis sí describen un cambio después del 2007: el riesgo de default toma más importancia durante y después del stress bancario. Esta investigación, al igual que el trabajo de Filipovic y Trolle (2012), usa los contratos swaps con el fin de refinar la descomposición del riesgo de default y no-default. Independiente de los resultados, se evidencia que el riesgo interbancario y sus hechos estilizados no han sido aun ampliamente documentados para los años posteriores a la crisis.
Este documento tiene como objetivo evidenciar los cambios que se presentaron en la estructura a plazos del riesgo interbancario de Estados Unidos durante la última crisis financiera y también cómo fue el comportamiento de los principales factores de dicha estructura. Algunos autores señalan que este riesgo tiene importantes implicaciones para los agentes del mercado, bancos centrales y policy makers. Por un lado, poder representar este riesgo en la forma de una estructura a plazos brinda una herramienta para entender las expectativas sobre un posible estado de stress en el mercado interbancario. Adicionalmente, brinda herramientas para los policy makers a la hora de evaluar, medir y controlar políticas en pro de controlar y mitigar este riesgo. Por último, sirve para que los administradores de riesgo puedan hacer pricing y hedging en el mercado de derivados de tasa de interés y de crédito.
Los resultados encontrados en esta investigación sugieren que se presentaron importantes cambios en las estructuras a plazos del riesgo interbancario y sus componentes. En los años previos a la crisis financiera de 2007-2008, el riesgo de no-default pertenecía a las dos terceras partes del riesgo interbancario. Con el inicio de la crisis, el riesgo interbancario y sus componentes repuntaron importantemente, pero este repunte se dio en mayor proporción para el riesgo de default. Los años de la crisis y los posteriores a ellos se caracterizan por tener un mayor riesgo de default en relación con el de no-default. Adicionalmente, se encuentra que la crisis financiera de 2007-2008 se caracterizó por ser un problema más de corto que de largo plazo en contraste con la crisis del euro de 2010.
El documento está estructurado de la siguiente forma: después de este apartado introductorio está la sección 1 que describe el modelo usado en la estimación, la sección 2 que presenta la metodología usada, la sección 3 que muestra algunos resultados encontrados, la sección 4 en la que se analizan los componentes del riesgo interbancario y, por último, la sección 5 en la que se concluye.
1. La estructura a plazo del riesgo interbancario
1.1. Instrumentos financieros
En el mercado existen dos tasas de interés instantáneas 5 : una tasa cubierta de riesgo de default rc (t) y otra expuesta a dicho riesgo r(t). La diferencia entre ellas radica en que la tasa cubierta o colateralizada tiene una prima por dicha protección, mientras que la otra no. En esta especificación se asume que dicha prima es constante y, por ende, la relación entre las dos tasas de interés es:
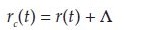 (1)
(1)donde rc (t) es la tasa de interés instantánea colateralizada, r(t) es la tasa no colateralizada y Λ corresponde a la prima de cobertura que mide la probabilidad de que el emisor de un título haga default 6 . En el anexo E se especifican los distintos valores asumidos en esta investigación sobre el valor de esta prima.
Siguiendo lo propuesto por Filipovic y Trolle (2012), para modelar el spread entre la Libor (IRS para los plazos mayores a 6 meses) y los OIS es necesario tener en cuenta el precio de dos títulos: un contrato colateralizado indexado a la tasa colateralizada rc (t) y un bono cero cupón como función de una tasa no colateralizada r(t).
Contrato colateralizado: un contrato colateralizado es aquel que le asegura a una de las partes la posibilidad de un evento de riesgo de default principalmente. En este caso, el contrato retorna una tasa de interés que tiene una prima usada como cobertura, en caso de un evento de impago. El precio de este contrato colateralizado PC (t,T), pactado en t con vencimiento en T y que paga un principal de $1 está expresado como:
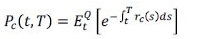 (2)
(2)El valor de este contrato va a depender de la medida martingala que se tome para calcular el valor esperado, en este caso, la medida martingala Q se conoce como la medida neutral al riesgo que asegura la inexistencia de posibilidades de arbitraje en la valoración de dicho instrumento. Adicionalmente, el precio de este contrato dependerá de la distribución de ʃ T t rc (s)ds y, por ende, del proceso que sigue r(t).
Bono cero cupón: un bono cero cupón indexado a una tasa no colateralizada r(t) se encuentra expuesto a la posibilidad de que el emisor haga default antes del vencimiento de la deuda, y, por ende, el pago del principal no sea pagado. Se denota el tiempo en que la compañía de referencia hace default. En caso de que no se presente el evento de default (τ< T), el total del principal será pagado al inversionista; en caso que sí se materialice este riesgo, se pagará un porcentaje Lgd % del pago total de dicho bono. Siguiendo lo propuesto por Filipovic y Trolle (2012), el precio de un bono cero cupón que se encuentra expuesto al riesgo de default está determinado por:
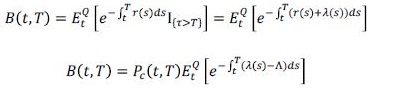 (3)
(3)donde λ(t) corresponde a la intensidad de default 7 del emisor del bono. Adicionalmente, se asume que la correlación entre la intensidad de default y las tasas de interés instantáneas es nula 8 . En este caso, el bono cero cupón dependerá no solo del proceso que se asume de la tasa de interés instantánea r(t) sino también de la distribución de y, más específicamente, del proceso asumido para las intensidades de default.
Las tasas instantáneas no son observables en el mercado. Por lo tanto, en este modelo, es usada como variable observada por la Libor, principal indicador del costo de fondeo de las operaciones interbancarias. Sin fricciones, la Libor correspondería a:
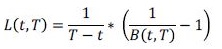 (4)
(4)Sin embargo, en el mercado se evidencias fricciones que se asocian principalmente con iliquidez o problemas de medición 9 , es por ello que es necesario que el modelo incluya un término que recoja dichas imperfecciones. La función Ξ(t, T) busca capturar dichas imperfecciones. De esta forma la Libor está expresada como:
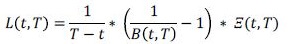 (5)
(5)Cabe notar que es Ξ(t, T) una función decreciente con respecto al vencimiento (T) y que cumple con la siguiente condición final:
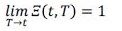 (6)
(6)Adicionalmente, esta función va a depender de una variable ξ(t) que describe el comportamiento del riesgo de no-default 10
Overnight Indexed Swap (OIS): Adicionalmente, se cuenta en el mercado con los contratos OIS. La tasa del OIS corresponde a:
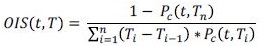 (7)
(7)Donde PC corresponde al precio del contrato colateralizado descrito anteriormente Ti y corresponde a los n plazos en que hay un pago del contrato OIS. Asumiendo que el número de pagos es único y corresponde al pago del principal, la tasa OIS termina siendo en su forma más sencilla:
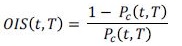 (8)
(8)Este tipo de contratos se caracterizan por tener un riesgo de default inferior a la Libor y los demás tipos de derivados de tasas de interés, por el hecho de que los OIS dependen del promedio de tasas prime, generalmente, la federal fund rates en el caso de Estados Unidos o la Eonia (European Overnigth Indexed Average) para el caso de Europa.
Restando la ecuación (4) y (8) y un poco de algebra, se obtiene el Libor-OIS spread:
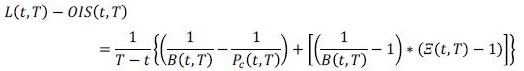 (9)
(9)En la especificación del modelo, y siguiendo lo propuesto por Filipovic y Trolle (2012), esta ecuación describe la estructura a plazos del riesgo interbancario para distintos vencimientos (T). El primer término corresponde al riesgo de default, mientras que el segundo al riesgo de no-default. Esta ecuación permite construir la estructura a plazos tanto del riesgo interbancario como de sus componentes.
Credit Default Swap (CDS): un contrato CDS es aquel que intercambia un flujo de cupones periódicos por un pago fijo que sirve como protección, en caso de que una entidad emisora haga default. Este contrato es firmado entre dos partes, de tal forma que la parte A (comprador) paga a la parte B (vendedora) una serie de cupones periódicos (Premium Leg) en busca de una protección ante un evento de default de la empresa C. En caso de que la empresa C haga default, la parte B pagará a A un porcentaje del valor del principal (Protection Leg).
Siguiendo lo propuesto por Brigo y Mercurio (2006), una forma sencilla de encontrar las intensidades de default implícitas en los spreads de los CDS es asumir que estas intensidades son constantes durante tramos (piecewise constant) de la forma:
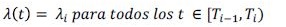 (10)
(10)para todos los i plazos existentes en el mercado. A partir de esta especificación, el pago de un CDS resulta ser la diferencia entre el Premium Leg y el Protection Leg y está expresado por 11 :
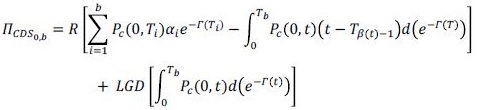 (11)
(11)donde Π es el payoff del CDS, b es el número de periodos en que el contrato de CDS está vigente, a corresponde a la periodicidad con que se hacen los pagos de la cobertura (asumido generalmente como pagos trimestrales, es decir α = 0,25), R es el valor de la prima pagada, Γ es la intensidad de default acumulada explicada en el Anexo A, Tβ(t)–1 corresponde a la fecha previa del pago de la cobertura dentro de la vigencia del CDS, PC es el precio de un contrato colateralizado presentado anteriormente y Q(t) es la función de supervivencia (survival probability) que está representada por:
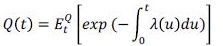 (12)
(12)En la bibliografía y en la práctica existen diversas formas de obtener las intensidades de default implícitas en los spreads de los CDS. Brigo, Mercurio, Guarin et al. (2014), entre otros, exponen distintas metodologías, generalmente, filtros no lineales que logran recuperar dichas intensidades. El objetivo de esta tesis no es filtrar las intensidades de default, sino entender los componentes del riesgo interbancario, entre ellos, el riesgo de default.
1.2. Modelo a partir de una representación affine 12
En el modelo existen tres principales variables, la tasa de interés instantánea r(t), la intensidad de default λ(t) y el parámetro de no-default ξ(t). Siguiendo lo propuesto por Filipovic y Trolle (2012), cada una de ellas sigue un proceso estocástico que define la trayectoria de cada una de estas variables.
La tasa de interés instantánea r(t) sigue un proceso de difusión de un único factor tipo CIR (Cox-Ingersoll-Ross) de la siguiente forma:
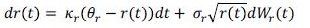 (13)
(13)donde kr corresponde a la velocidad de reversión a la media de largo plazo Ξ r , σ r , es la volatilidad del proceso Wr (t) y es un movimiento browniano estándar. Adicionalmente, esta especificación asume un parámetro adicional ψ que transforma un proceso browniano bajo la medida martingala Q a la medida objetiva P 13 . La representación affine del precio de un contrato colateralizado de la ecuación (2) viene representada por 14 :
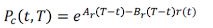 (14)
(14)Por otro lado, el factor de no-default Ξ(t, T) está expresado como:
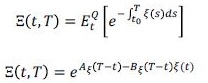 (15)
(15)donde la variable ξ(t) es no observable en el modelo y explica los movimientos del componente residual de la Libor y del riesgo de no-default. Esta variable ξ(t) sigue un proceso CIR de la siguiente manera:
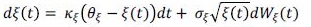 (16)
(16)En este modelo, a intensidad de default λ(t) no sigue un proceso de difusión, ya que su estimación es el resultado de encontrar una intensidad implícita en los spreads de los CDS existentes en el mercado (ver anexo A). Sin embargo, sí es necesario resaltar que la prima Λ de la ecuación (1) se puede entender como un valor de largo plazo de un proceso de difusión de las intensidades de default.
2. Metodología
El modelo presentado anteriormente se caracteriza por depender de variables latentes o no observables en el mercado, las cuales son la tasa de interés instantánea r(t), la intensidad de default λ(t) y la variable de no-default ξ(t). Todas estas variables dependen de un activo que sí es observable y, por ende, es necesario extraer dichas variables no observables, denominadas ‘estado’, de las cotizaciones de activos que sí son observables. Adicionalmente, no se conocen los parámetros del modelo, por lo que es necesario hacer la estimación de dichos parámetros.
El problema de estimación y filtración se resuelve siguiendo lo propuesto por Wan y van der Merwe (2000), donde se filtra la variable estado en cuestión y simultáneamente se estiman los parámetros del proceso de dichas variables. La estimación se hace por medio de máxima verosimilitud. Para la filtración, se usa un filtro no lineal llamado Unscented Kalman Filter 15 . A diferencia del filtro de Kalman estándar (lineal), el unscented permite tener interacciones no lineales entre las variables en la representación estado espacio (ver anexo C). Esta estimación se hace en dos etapas: la primera busca estimar los parámetros relacionados con la tasa de interés instantánea y filtrar dicha variable; en la segunda etapa, se estima y se filtra lo relacionado con la variable de no-default. Entre las dos etapas existe un paso intermedio donde se incluyen las intensidades de default (explicadas de acuerdo con el anexo A), según la especificación de la ecuación (3). La forma como se llevó a cabo la metodología de filtración y estimación está expuesta en el anexo C.
Para la estimación, fueron necesarias las series de la Libor (vencimiento en 3 y 6 meses en dólares), las tasas de los IRS, OIS, CDS para vencimientos a 3 y 6 meses, 1, 2, 3, 4, 5 y 10 años, las tasas de los Federal Funds y los repos overnight de la reserva federal de Estados Unidos. Estos datos fueron extraídos de la plataforma Bloomberg. Todas estas series tuvieron una periodicidad diaria y fueron tenidos en cuenta desde octubre de 2006 hasta diciembre de 2012, contando con un total de 1336 datos que abarcan el periodo anterior a la crisis financiera subprime, hasta después de la crisis de la zona euro de 2010. La importancia de contar con estos periodos se debe a que los objetivos de la presente investigación se centran en analizar los cambios y las interacciones de los distintos riesgos de la estructura a plazos del riesgo interbancario antes y después de las crisis.
Una de las características de la presente investigación es que se centra en el riesgo del mercado interbancario como un agregado de este mercado, en cambio de analizar una partición de bancos pertenecientes a este. Para cuantificar el riesgo de default, es necesario contar con un índice que agrupe el comportamiento de los CDS de cada banco perteneciente al panel de la Libor. Sin embargo, existe la dificultad de contar con este índice y que cumpla con dos condiciones: (i) incluya los periodos previos y posteriores a la crisis, incluidos en esta investigación y (ii) sea de fácil acceso 16 . Para solucionar este problema, fue necesario construir un índice que recoja la evolución de los CDS de los bancos pertenecientes al panel de la Libor pero de la manera más simple. Dicho índice consiste en un promedio simple de CDS de los bancos pertenecientes al panel de la Libor con vencimientos a 1, 2, 3, 4, 5 y 10 años. La estructura de CDS está resumida en el anexo D.
3. Resultados
3.1. Parámetros estimados
Los parámetros encontrados a partir del proceso de estimación expuesto en la sección 2 y el anexo C se presentan en la tabla 1. Adicionalmente, estas estimaciones son comparadas con los resultados de Filipovic y Trolle (2012) en el anexo F 17 .
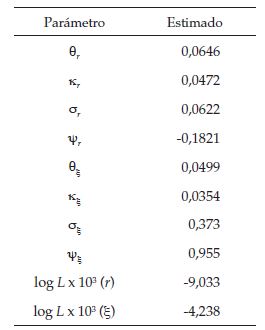
Los resultados encontrados en esta investigación sugieren que la tasa de interés es menos volátil que el parámetro de no-default. La tasa de interés de largo plazo se encuentra cercana al 6,5 % y esta converge más rápido que el parámetro de no-default. Los valores de ψ, entendido como el precio del riesgo en el mercado, son negativos para ambas variables estado, resaltando la existencia de una prima requerida por los agentes del mercado por tener una exposición a movimientos en la tasa de interés.
3.2. Variables estado
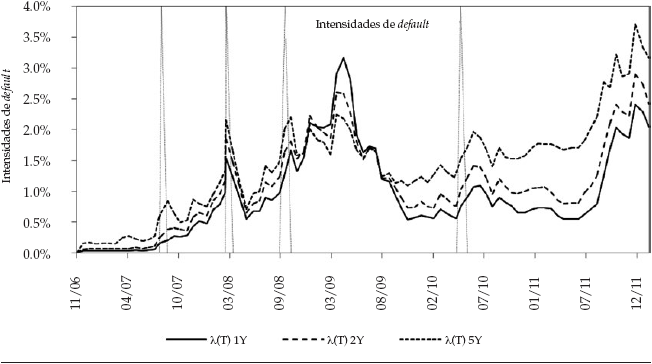
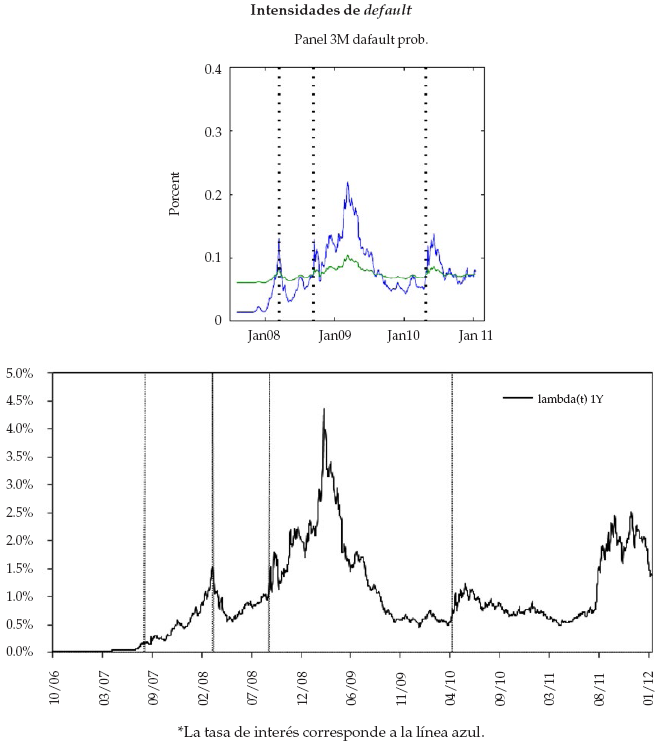
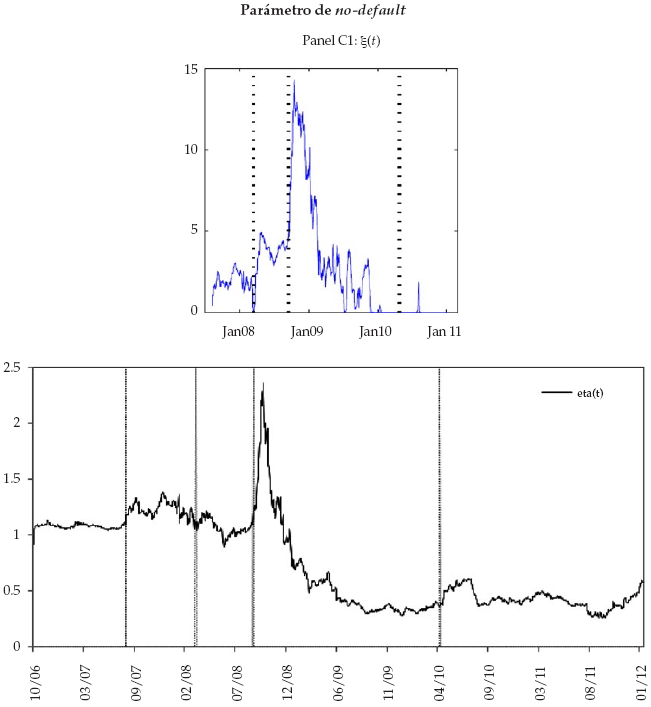
El comportamiento de las tres variables estado (tasa de interés r(t), intensidades de default λ(t) y parámetro de no-default ξ(t)) filtradas y estimadas según la metodología de la sección 2, son mostradas en la figura 2.
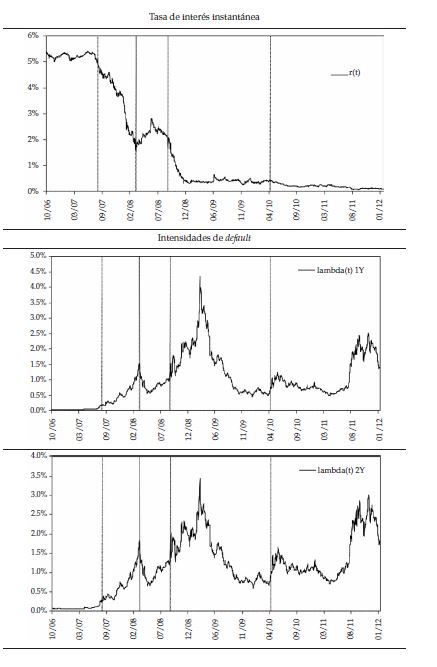
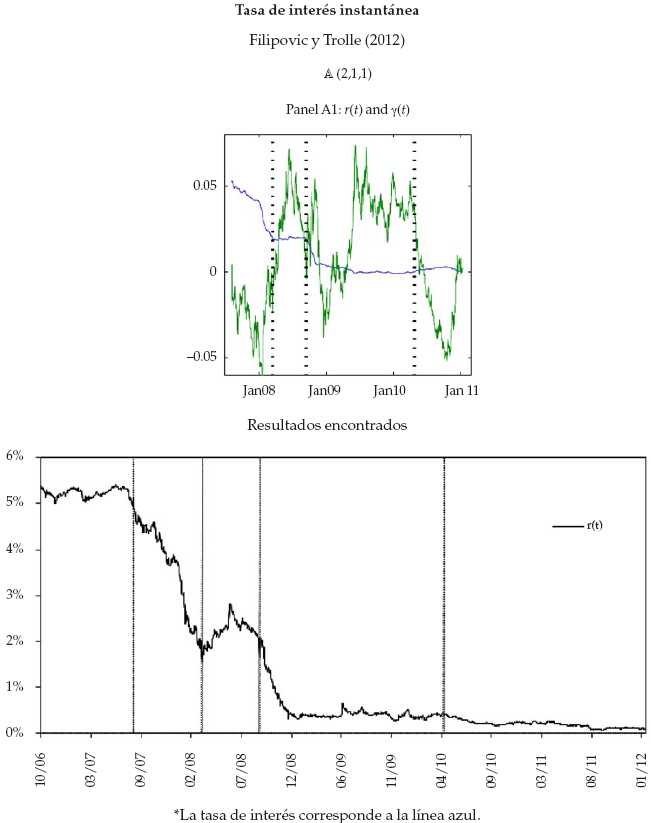
Todas las variables tuvieron un comportamiento distinto durante la crisis financiera y los resultados son similares a los encontrados por Filipovic y Trolle (2012). En el panel superior de la figura 2 se presenta el comportamiento de la tasa de interés instantánea r(t). Esta sigue, principalmente, el comportamiento de la tasa de los OIS y estos, a su vez, la tasa de la política monetaria de la Reserva Federal de Estados Unidos 18 . Del comportamiento de la tasa de interés instantánea se destacan varios hechos: la crisis financiera llegó con una relajación cuantitativa por parte de la autoridad monetaria norteamericana; la Reserva Federal redujo sus tasas prime en 263 pb desde el 8 de agosto de 2007 hasta el 5 de enero de 2008. Como resultado, se presentó una reducción de los costos de fondeo y de las tasas de interés del mercado. En los días donde la crisis se encontraba en su punto más agitado, a mediados de 2008, los costos de fondeo (Libor) no respondieron igual que la tasa de política monetaria de Estados Unidos y se evidencia un aumento considerable en el riesgo interbancario por la vía de un aumento en la tasa de interés desde la venta de Bear Stearns hasta la quiebra de Lehman Brothers; finalmente, la tasa de interés se ha mantenido en niveles históricamente mínimos, lo que coincide con los mínimos históricos de la tasa de política de la Fed.
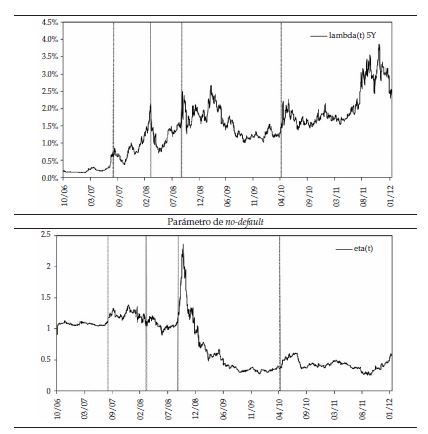
En el panel intermedio se presentan las intensidades de default implícitas en los spreads de los CDS para los plazos a 1, 2 y 5 años 19 . La intensidad de default con plazo a un año tiene un promedio de 0,954 %, con un mínimo de 0,031 % y un máximo de 4,367 % alcanzado en marzo de 2009; la intensidad de default con plazo a dos años tiene un promedio de 1,109 %, alcanzando un mínimo de 0,065 % y el máximo en marzo de 2009 hasta 3,437 %; por último, las intensidades de default implícitas en los CDS con vencimiento a cinco años alcanzaron un máximo de 3,873 % en noviembre de 2011 y un mínimo de 0,141 % con un promedio de 1,428 %. Se puede apreciar que las intensidades de default de los CDS de más corto plazo fueron más sensibles durante la crisis financiera, alcanzaron máximos más altos durante los días más difíciles de la crisis, pero volvieron más rápidamente a niveles bajos después de la crisis financiera 20 . Durante algunos momentos de la crisis financiera, la estructura a plazos de los CDS tomó pendiente negativa, lo que indicó que las expectativas que tenía el mercado de un evento de default por parte de una entidad bancaria eran un problema más de corto que de largo plazo; en contraste, en la crisis europea de 2010, sí se acentuó más como un problema de largo que de corto plazo. Las intensidades de default alcanzaron máximos durante la crisis financiera, con fuertes cambios en las estructuras a plazos del riesgo de default, las intensidades de default y los spreads de los CDS. En los años posteriores a la crisis, ni los CDS ni las intensidades de default han vuelto a registrar los niveles de los años previos a la crisis financiera de 2008, incluso durante la crisis del euro de 2010.
Por último, el comportamiento del parámetro de riesgo de no-default no tuvo importantes cambios hasta la quiebra de Lehman Brothers, donde las condiciones de liquidez de algunos bancos y del mercado interbancario en general tuvieron importantes deterioros. Posterior a la crisis, este indicador estuvo por debajo de los niveles previos a esta, lo que evidenció la pérdida de relevancia del riesgo de no-default en el riesgo interbancario con respecto a los indicadores de riesgo de default que sí presentaron importantes cambios después de 2008.
En línea con lo propuesto por Filipovic y Trolle (2012), la pendiente negativa en la estructura a plazos observada a finales de 2008 está explicada por un aumento considerable en el riesgo de default y la pérdida de relevancia en el riesgo de no-default. Lo anterior está soportado en la estructura a plazos de los CDS que tomaron una pronunciada pendiente negativa y en la estructura de las intensidades de default (ver anexo D).
Sin duda alguna, la estructura a plazos del riesgo interbancario sufrió importantes cambios durante la crisis financiera de 2008. Este hecho surgió debido a que la crisis de 2008 se gestó en el mercado bancario estadounidense y, posteriormente, las expectativas negativas de todos los riesgos (interbancario, default, liquidez, mercado, entre otros) se expandieron a todos los sectores de la economía. Los resultados demuestran que los cambios en los años posteriores a la crisis tuvieron un carácter más estructural que temporal.
4. Componentes del riesgo interbancario
4.1. Descomposición de la estructura a plazos
La estructura a plazos del riesgo interbancario se descompone en dos riesgos principalmente: el riesgo de default y el riesgo de no-default. El riesgo de default hace alusión a las posibles pérdidas que puedan registrar los inversionistas y los bancos, derivadas de eventos de default de la entidad emisora de un título de deuda. Por otro lado, el riesgo de no-default está fuertemente relacionado, como se había mencionado anteriormente, con el riesgo de liquidez. La forma como se hace la separación de este riesgo puede variar y llegar a ser sensible a la especificación que se haga; sin embargo, al no contar con una metodología estándar ni aceptada para dicha partición, se sigue lo propuesto por Filipovic y Trolle (2012) que separa los componentes del riesgo interbancario a partir de las mismas ecuaciones acá presentadas. Partiendo de la ecuación que describe la estructura a plazos del riesgo interbancario (ecuación (9)), el riesgo de default corresponde al primer término y el riesgo de no-default al segundo.
En este orden de ideas, el componente de default se mide mediante un spread teórico que existiría si se materializara únicamente el riesgo de default en la estructura a plazos del riesgo interbancario (este spread corresponde a igualar Ξ(t,T) = 1). La estructura a plazos del riesgo de default está descrita por:
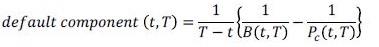 (17)
(17)Este componente va a ser siempre positivo por el hecho de que se cumple con λ > 0 en conjunto con la ecuación (3). Este spread resulta estar fuertemente influenciado por el diferencial entre el bono cero cupón B(t,T) y el precio de un contato colateralizado PC (t,T). Este diferencial, y por ende el default component, va a depender de la distribución de Γ(t) = ʃt 0 λ(u)du Más específicamente, el riesgo de default es una función creciente con las intensidades de default λ(t).
Por otro lado, el riesgo de no-default resulta ser el segundo término de la ecuación (9) y corresponde al valor de la estructura a plazos del riesgo interbancario en el caso de que no exista riesgo de default (λ(t)=0). La estructura a plazos del riesgo de no-default está medida por:
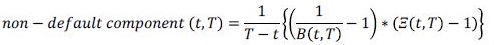 (18)
(18)Al igual que el riesgo de default, el de no-default también será positivo por el hecho Ξ(t,T) > 1 que y con entonces B(t,T) < 1.
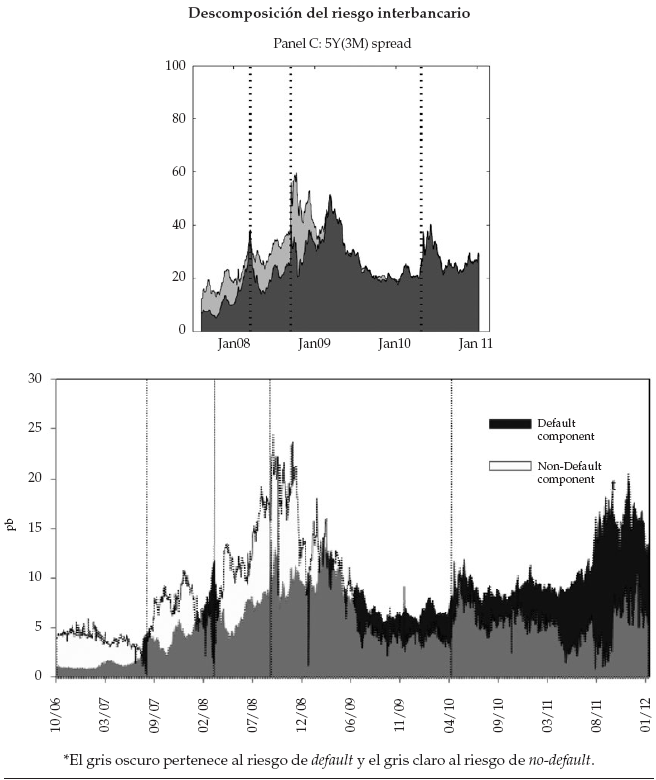
Con el fin de poder analizar los cambios sufridos por cada componente del riesgo interbancario a raíz de la crisis financiera, el periodo de análisis se dividió en tres sub-grupos: el periodo precrisis (antes de la quiebra de la venta de Bear Stearns), el periodo de la crisis (desde la quiebra de Bear Stearns hasta principios de 2010) y el periodo poscrisis. Si se evalúan los riesgos para todo el periodo de la muestra, se puede incurrir en el error de no tener en cuenta que después del inicio de la crisis existió un importante cambio estructural en todas las variables. La magnitud de los componentes del riesgo interbancario a lo largo de cada estructura a plazos se resume en la tabla 2 y en la figura 3.
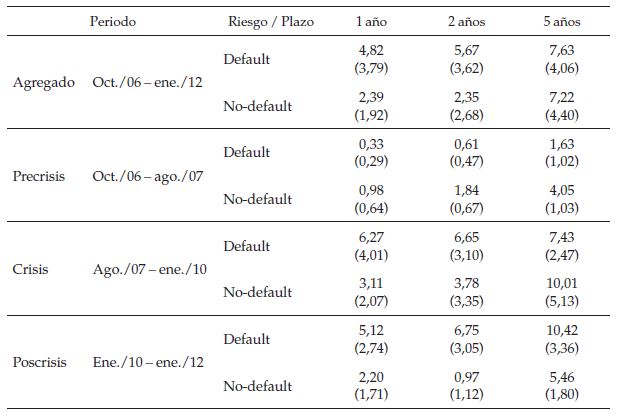
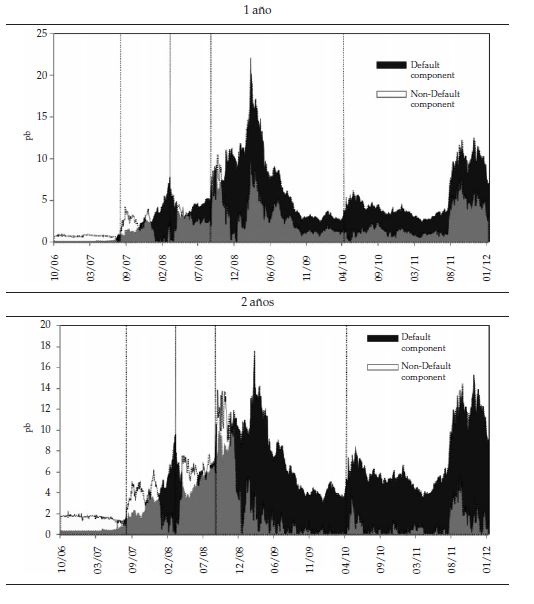
Se puede apreciar que en los plazos más largos ambos riesgos aumentan para todos los subperiodos. El periodo precrisis se diferencia de los demás periodos en que registra los niveles más bajos en los componentes del riesgo interbancario para todos los plazos tenidos en cuenta. Adicionalmente, antes de la crisis financiera, el riesgo de no-default era casi tres veces mayor que el riesgo de default a lo largo de toda la estructura a plazos. En las semanas donde la crisis se agudizó, ambos riesgo aumentaron considerablemente y ayudaron mutuamente a que la estructura a plazos del riesgo interbancario aumentara considerablemente. En promedio, el riesgo de default dobló al de no-default para los plazos más cortos en la estructura a plazos durante los últimos meses de 2008 y principios de 2009. Lo anterior sustenta la hipótesis de que el riesgo de default tomó más relevancia que el de no-default en el corto plazo durante la crisis. Posterior al 2010, los niveles de ambos riesgos fueron inferiores a los registrados durante la crisis, pero superiores a los periodos previos a la crisis. Sin duda alguna estos resultados evidencian los importantes cambios que sufrió la estructura a plazos del riesgo interbancario durante la segunda parte de la década pasada. Estos resultados sugieren también que el riesgo de default es más volátil que el riesgo de no-default en el corto que en el largo plazo. Filipovic y Trolle (2012) sugieren que esto se debe a que los participantes del mercado percibían las altas exposiciones al riesgo de default más como un fenómeno de corto que de largo plazo. Adicionalmente, el riesgo de default alcanzó máximos durante la crisis para los periodos de más corto plazo, mientras que los plazos más largos alcanzaron máximos durante la crisis de la deuda soberana europea de 2010.
4.2. ¿Qué dice el riesgo de default?
Los periodos previos a la crisis se caracterizaron por tener un bajo riesgo de default. Posterior al inicio de la crisis financiera, este riesgo aumentó considerablemente para todos los plazos. Durante los meses más agudos de la crisis, la estructura a plazos del riesgo de default aumentó en mayor proporción para los plazos más cortos. Este último alcanzó 22,11 pb en marzo de 2009, por encima en 8 puntos pb registrados para el vencimiento a 5 años que fue de 14,18 para la misma fecha. Lo anterior se resume en una pendiente negativa en la estructura a plazos del riesgo de default. Esto se puede observar en la figura 4 donde se dibuja el riesgo de default derivado del modelo para distintos plazos y a lo largo de los años incluidos en esta investigación.
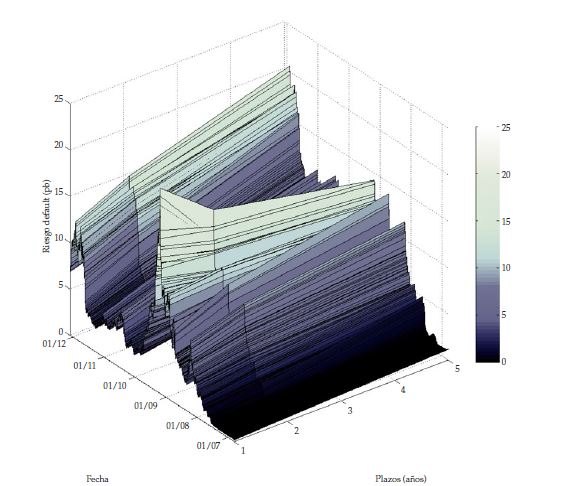
La estructura a plazos con pendiente negativa se presentó debido a las expectativas que tenían los agentes del mercado sobre los efectos de un evento de default de algunos bancos en Norteamérica. Para marzo de 2009 ya algunos bancos e instituciones financieras en Estados Unidos habían presentado un evento de default 21 , por lo que los agentes tenían expectativas de la existencia de quiebras adicionales de algunas instituciones financieras, pero suponían que, en el largo plazo, los gobiernos entrarían a rescatar estas instituciones. Este rescate finalmente sucedió con la aprobación de la ‘Emergency Economic Stabilization Act’ (Ley de Estabilización Económica de Urgencia), una ley cuyo único objetivo era la compra de activos basura a los bancos nacionales en Estados Unidos para sacarlos de la quiebra. Posterior a la aprobación de esta ley, el riesgo de default se redujo drásticamente y la estructura a plazos volvió a tener pendiente positiva. Sin embargo, nunca se volvieron a registrar los niveles previos a la crisis financiera. El riesgo de default volvió a repuntar durante la crisis de la zona euro, donde algunos países estuvieron cercanos a hacer default debido a altos niveles de endeudamiento gubernamental. Durante esta última crisis, el riesgo de default aumentó en mayor proporción para los plazos más largos, contrario a la crisis subprime de 2008. Durante la crisis del euro, el riesgo de default a cinco años alcanzó su máximo.
4.3. ¿Qué dice el riesgo de no-default?
Al igual que con el riesgo de default, el modelo permite construir la evolución del riesgo de no-default para distintos plazos durante todo el periodo de estudio. La estructura a plazos resultante del modelo se puede observar en la figura 5.
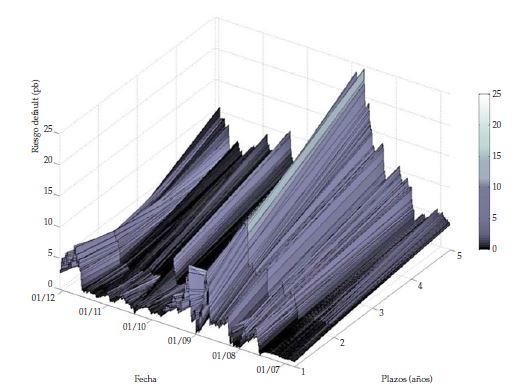
Durante todo el periodo de estudio, la estructura a plazos del riesgo de no-default tuvo pendiente positiva, aún durante la crisis financiera y del euro en 2010. Para finales de 2008 y principios de 2009, donde la crisis financiera fue más aguda, el riesgo de no-default alcanzó 10 pb en el corto plazo y hasta 24 pb en el largo plazo para septiembre de 2008. A diferencia del riesgo de default, el riesgo de no-default volvió rápidamente a niveles cercanos a los años anteriores a la crisis y registró los mismos niveles, de hecho para los plazos más cortos el riesgo de no-default posterior a la crisis fue inferior a los registrados en el 2006. Los años siguientes a la crisis se registraron niveles de riesgo inferiores a los 5 pb. Estos resultados sugieren que el riesgo de no-default tuvo efectos temporales durante la crisis, pero posteriormente se normalizaron a los niveles previos a la crisis. Adicionalmente, se evidencia la pérdida de relevancia del riesgo posterior a la crisis frente al riesgo de default.
Por otro lado, es necesario entender cómo el riesgo de no-default estimado en esta investigación se relaciona con la liquidez del mercado. Siguiendo lo propuesto por Brunnermeier y Pedersen (2009), la liquidez del mercado interbancario tiene una estrecha relación con la liquidez de las operaciones de fondeo que los corredores llevan a cabo en este mercado. Dado que no se cuenta con una medida exacta de la liquidez de estas operaciones de fondeo, se construye un spread que logre representar en buena proporción la facilidad con la que estas operaciones se hacen a precios de mercado, pero de la manera más eficiente y sin incurrir en sobre costos, resultado de la inexistencia de contrapartes en dichas operaciones. Fointaine y Garcia (2011) construyen un indicador de liquidez (TED Spread) resultante de la diferencia entre la Libor a 3 meses y los Tbills del tesoro de Estados Unidos. Este spread está representado en la figura 6.
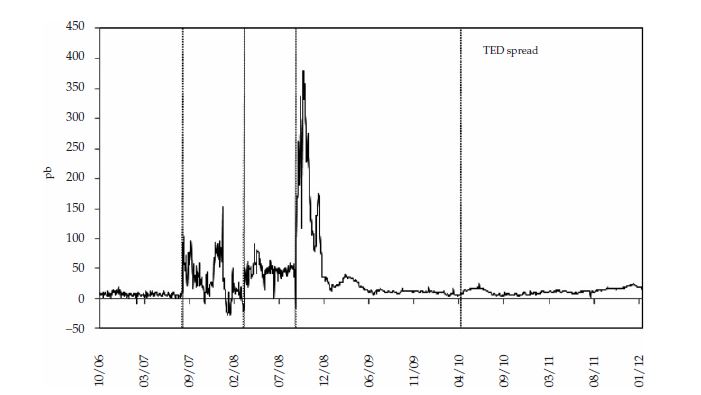
Ellos concluyen que aumentos en este spread es síntoma de una reducción en la liquidez de las operaciones de fondeo, vía efectos sobre la curva de los tesoros americanos y la de la Libor. Esto se resume en el riesgo de fondeo, que es la exposición a la dificultad de poder contar con un mercado profundo para encontrar liquidez y así fondear los papeles que se tengan en la posición de los bancos. Como se puede observar en la figura 6, la liquidez en el mercado interbancario se vio fuertemente contraída durante la crisis, pero llegó a su punto más agudo en octubre de 2008 cuando el spread de liquidez alcanzó casi 400 pb. En estos meses, la crisis estaba consumida y se encontraba en su punto más agudo; las autoridades monetarias de Estados Unidos tenían como único objetivo sacar la economía de la crisis financiera, y la forma como atacaron esta situación fue inyectando una gran cantidad de liquidez al mercado, reduciendo las tasas de corto plazo y aplicando políticas como el ‘Emergency Economic Stabilization Act’. Posterior a la crisis, la liquidez volvió a niveles bajos nuevamente y no repuntó durante la crisis del euro en 2010. Estos resultados se soportan en la hipótesis de que el riesgo de no-default tuvo efectos temporales durante la crisis, que rápidamente se desvanecieron.
Para analizar la relación entre el riesgo de no-default y el indicador de liquidez construido a partir de la Libor y los Tbills (TED Spread), es necesario saber qué proporción de dicho indicador está libre de los efectos del riesgo de default 22 . Para ello, se hace una regresión entre el indicador y los dos primeros componentes de la estructura a plazos de los CDS; por construcción, el residuo de dicha regresión está libre de riesgo de default. Por último, para cuantificar la relación entre el TED spread y el riesgo de no-default, se hace una regresión entre el parámetro ξ(t) y el residuo libre de default 23 . El coeficiente de la estimación es 0,0455 y es significativo al 1 % de nivel de confianza; el R2 es de 0,0413. La correlación entre estas dos variables es positiva e igual a 0,574. Estos resultados van en línea con lo propuesto por Filipovic y Trolle (2012), quienes encuentran que el coeficiente de la regresión está entre 0,039 y 0,034 con una correlación de 0,63.
Los resultados anteriores sugieren que el componente de no-default en la estructura a plazos del riesgo interbancario captura en gran proporción los efectos de iliquidez libres de riesgo de default en el mercado interbancario. Lo anterior va en línea con lo encontrado por Filipovic y Trolle (2012).
5. Conclusiones
Esta investigación tiene como principal objetivo analizar la existencia de los cambios que se dieron en la estructura a plazos del riesgo interbancario de Estados Unidos durante la crisis financiera de 2007-2008. Adicionalmente, se analizaron los riesgos que componen el riesgo interbancario. Este riesgo se mide mediante la aproximación propuesta por Filipovic y Trolle (2012), donde se construye un spread (Money Market Spread) resultante entre la Libor (con vencimiento a 3 meses) y los OIS. Las expectativas para distintos plazos del riesgo interbancario están medidas por el spread (Swap Spread) resultante entre los IRS y los OIS. A partir de estos spreads, se construyó una estructura a plazos del riesgo interbancario, dinámica para todo el periodo de estudio (octubre de 2006 hasta diciembre de 2012). Se encontró que el riesgo interbancario repuntó considerablemente, justo con el inicio de la crisis financiera en agosto de 2007, pero este repunte ocurrió, en mayor proporción, en el Money Market Spread que en el Swap Spread, lo que evidenció una pronunciada pendiente negativa de la estructura a plazos del riesgo interbancario. Sumado a esto, el modelo permite separar el riesgo de default del riesgo de no-default implícito en los spreads. Al hacer esta separación entre sus componentes, se encuentra que desde el inicio de la crisis, el riesgo de default condujo a ese importante repunte de los swap, mientras que el riesgo de no-default perdió relevancia dentro de la estructura a plazos del riesgo interbancario en los años de la crisis y posterior a ella. El repunte de los spreads, el riesgo interbancario y sus componentes encontraron su punto más agudo en marzo de 2009, después de la quiebra de algunos de los bancos importantes en el mercado interbancario estadounidense. Durante algunos días cercanos a esa fecha, el riesgo interbancario y el riesgo de default tuvieron una pronunciada pendiente negativa de la estructura a plazos, lo que evidenció que los agentes del mercado tenían expectativas de que la situación de stress financiera fuera un fenómeno más de corto que de largo plazo. Para enero de 2010, la percepción a los riesgos interbancarios y de default se estabilizaron, pero en niveles superiores a los registrados en los años previos al inicio de la crisis financiera. Por último, la crisis del euro se caracterizó por ser un problema más de largo que de corto plazo, contrario a la crisis financiera de 2008, y que desestabilizó nuevamente la estructura a plazos de los componentes del riesgo interbancario, principalmente la del riesgo de default.
Agradecimientos
A Rafael Serrano y a Carlos Castro por su ayuda en la elaboración e ideas aportadas a la tesis. No recibí ayuda financiera en la elaboración del documento. Este documento hizo parte de la tesis de grado de la maestría en Finanzas Cuantitativas de la Universidad del Rosario.
Referencias
Andrews, A., & Grewal, M. (2008). Kalman Filtering. Theory and Practice Using MATLAB. New Yersey: John Wiley & Sons.
Angelini, P., Nobili, A., & Picillo, M. (2009). The interbank market after August 2007: what has changed and why? Bank of Italy, Working Papers 731.
Bianchetti, M. (2009). Two Curves, One Price: Pricing & Hedging Interest Rate Derivatives Decoupling Forwarding and Discounting Yield Curves. Risk Magazine.
Bolder, D. (2001). Affine Term-Structure Models: Theory and Implementation. Bank of Canada, Working Papers 15.
Bongaerts, D., Jong F. de, & Driessen J. (2011). Derivative princing with liquidity risk: Theory and evidence from credit default swap market. Journal of Finance, 66, 203-240.
Brigo, D., & Alfonsi, A. (2005). Credit default swap calibration and option pricing with the SSRD stochastic intensity and interest rate model. Finance and Stochastics, IX(1), 29-42.
Brigo, D., & Mercurio, F. (2006). Interest Rate Models - Theory and Practice. Milano: Springer.
Brunnermeier, M., & Pedersen, L. H. (2009). Market liquidity and funding liquidity. Review of Financial Studies, 22, 2201-2238.
Carr, P., & Wu, L. (2007). Theory and Evidence on the Dynamic Interactions Between Sovereign Credit Default Swaps and Currency Options. Journal of Banking and Finance, 31, 2383-2403.
Carr, P., & Wu, L. (2010). Stock Options and Credit Default Swaps: A Joint Framework for Valuation and Estimation. Journal of Financial Econometrics, 8(4), 409-449.
Cho-Hoi, H., Chung, T-K., & Chi-Fai L. (2010). Interest rate derivatives Princes to estimate Libor-Ois Spread dynamics and systemic funding liquidity shock probabilities. Hong Kong Monetary Autorithy, Working Papers Series 1004.
Christoffersen, P., Jakobs, K., Karoui, L., & Mimouni, K. (2009). Non-linear filtering in affine term structure models: Evidence from the term structure of swap rates. McGill University, Working paper.
Collin-Dufresn, P., & Solnik, B. (2001). On the term structure of default premia in the swap and LIBOR markets. Journal of Finance, 56, 1095-1116.
Cui, J., In, F., & Maharaj, E. A. (2012). What drives the Libor-Ois spread? From five major currency Libor-Ois spreads. Recuperado de SSRN: http://ssrn.com/abstract=2173944 or http://dx.doi.org/10.2139/ssrn.2173944
Denault, M., Gauthier, G., & Simonato, J. (2009). Estimation of Physical Intensity Model for Default Risk. The Journal of Futures Markets, 29, 95-113.
Duan, J., & Simonato, J. (1999). Estimating and Testing Exponential-Affine Temr Structure Models by kalman Filter. Review of Quantitative Finance and Accounting, 13(2), 111-135.
Duffie, D., Filipovic, D., & Schachermayer, W. (2003). Affine processes and applications in finance. Annals of Applied Probability, 13, 984-1053.
Duffie, D., & Huang, M. (1996). Swapt rates and credit quality. Journal of Finance, 51, 921-950.
Duffie, D., & Singelton, K. (1997). An econometric model of term structure of interest rate swap yields. Journal of Finance, 52, 1287-1323.
Duffie, D., & Singelton, K. (1999). Modeling term structure of defaultable bonds. Review of Financial Studies, 12, 687-720.
Duffie, D., & Singelton, K. (2003). Credit Risk: Pricing, Measurement and Management. Princeton: Princeton University Press.
Eisenschmidt, J., & Tapking, J. (2009). Liquidity Risk Premia in unsecured Interbank Money Markets. European Central Bank, Working Paper Series, 1025.
Feldhütter, P., & Lando, D. (2008). Decomposing swap spreads. Journal of Financial Economics, 88(2), 375-405.
Filipovic, D., & Trolle, A. (2012). The Term Structure of Interbank Risk. Swiss Finance Institute Research Paper No. 11-34. Filipovic, D. Term Structure Models - A Graduate Course. Viena: Springer.
Fontaine, J., & Garcia, R. (2011). Bond liquidity premia. Bank of Canada, Working Paper 2009-28.
Fujii, M., Shimada, Y., & Takahashi, A. (2009). A market model of interest rates with dynamic spreads in the presence of collateral and multiple currencies. Shinsei Bank and University of Tokyo, Working paper CIRJE-F-698.
Guarin, A., Liu, X., & Ng, W-L. (2014). Recovering default risk from CDS spreads with a nonlinear filter. Journal of Economic Dynamics and Control, 38, 87-104.
Iacus, S. (2008). Simulation and Inference for Stochastic Differential Equations. Milano: Springer.
Jeanblanc, M., Yor M., & Chesney M. (2009). Mathematical Methods for Financial Markets. Londres: Springer.
Johannes, M., & Sundaresan, S. (2007). The impact of Collateralization on Swap Rates. Journal of Finance, 62(1), 383-410.
Julier, S., & Uhlmann, J. (2004). Unscented Filtering and Nonlinear Estimation. Proceedings of the IEEE, 92(3).
Lando D. (2004). Credit risk modeling: Theory and Applications. Princeton: Princeton University Press.
Liu J., Longstaff F., & Mandell R. (2006). The market price of risk in interest rate swaps: The roles of default and liquidity risks. Journal of Business, 79, 2337-2359.
McAndrews J., Sarkar A., & Wang Z. (2008). The effect of the term auction facility on the London Inter-Bank Offered Rate. Federal Reserve Bank of New York, Working paper 335.
Mercurio, F. (2009). Interest rates and the credit crunch. New formulas and market models. Bloomberg, Working paper 2010-01.
Michaud F.-L., & Upper C. (2008). What drives interbank rates? Evidence from the Libor panel. BIS Quarterly Review, marzo, 47-58.
Platen E., & Bruti-Liberati N. (2010). Numerical Solution of Stochastic Differential Equations with Jumps. Londres: Springer.
Schwartz K. (2010). Mind the gap: disentangling credit and liquidity in risk spreads. The Wharton School, University of Pennsylvania, Working paper.
Taylor J. B., & Williams J. C. (2009). A black swan in the money market. American Economic Journal, Macroeconomics, 1, 58-83.
Varona, J. L. (1991). Métodos clásicos de resolución de ecuaciones diferenciales ordinarias. Logroño: Universidad de la Rioja.
Wan E., & van der Merwe R. (2000). The Unscented Kalman Filter for Nonlinear Estimation. Proceedings of Symposium 2000 on Adaptive Systems for Signal Processing, Communication and Control (AS-SPCC).
Wu T. (2008). On the Effectiveness of the Federal Reserve’s New Liquidity Facilities. Federal Reserve Bank of Dallas, Working Papers 0808.
Zhou R. (2008) Bond Implied CDS Spread and CDS-Bond Basis. Recuperado de SSRN: http://ssrn.com/abstract=1265548
Anexo A
Derivación fórmulas de valoración de los CDS e intensidades de default La forma como se obtienen las intensidades de default a partir de los spreads de los CDS puede variar dependiendo de las metodologías y de los supuestos que se hagan del modelo. Para esta investigación, se sigue lo propuesto por Brigo y Mercurio (2006), donde se construye una estructura a plazos de las intensidades de default con la particularidad de que son constantes entre los plazos disponibles en las cotizaciones que se observan en el mercado. A estas intensidades se les conoce como Piecewise Constant Intensity. Las intensidades de default para este tipo de modelos son procesos de Poisson homogéneos en el tiempo. En el mercado existen precios de CDS para los vencimientos T = {T 1, T 2,…, Ti ,…}. A partir de estos vencimientos se pueden encontrar las intensidades de default constantes durante cada plazo de la siguiente manera:
λ(t) = λt para t ϵ [Ti -1,Ti) (λ 1, λ 2, … , λi , …)
El payoff de un CDS se compone de una pata receptora y otra pagadora expresada de la siguiente manera:

La pata pagadora corresponde al Premium Leg que equivale al flujo de pagos que hace A a B periódicamente con el fin de cubrirse ante la eventualidad de un evento de default por parte de la empresa emisora de la deuda C (no mostrada en el gráfico). Por otro lado, el Protection Leg corresponde al pago que hace B a A en caso de que C haga default antes de la fecha de vencimiento del contrato. El payoff de un CDS resulta ser:
Payoff (Π) = Premium Leg – Protection Leg
donde:
Premium Leg
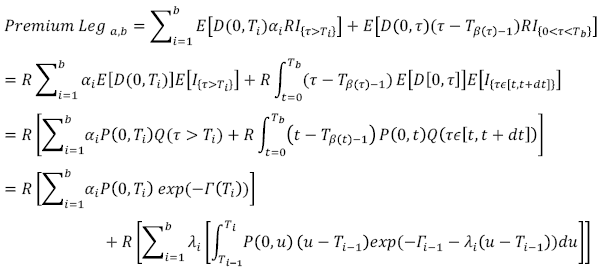
Protection Leg
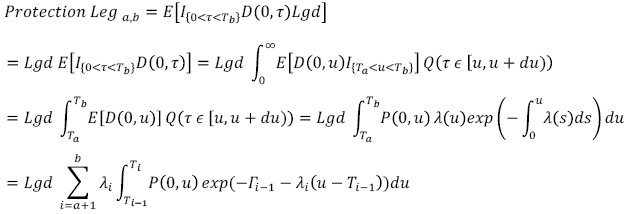
con λ i la intensidad de default para el plazo i, α i la periodicidad con la que se pagan las primas de protección, Γ(t) = ʃt 0 λ(u)du es la intensidad acumulada o hazard function con distribución Γ(r) = ε ~ exp(1). El algoritmo mediante el cual se encuentran las intensidades de default consiste en encontrar Γ(Tb ) a partir de Tb = T 1, posteriormente, para Γ(T 2) teniendo en cuenta λ1 y así sucesivamente para todos los vencimientos disponibles en el mercado. Al final, la estructura de las intensidades de default para una fecha dada tiene la siguiente representación:
Anexo B
Representación affine de la estructura a plazos del riesgo interbancario En esta sección se presenta la representación affine usada en el modelo que se basa en Duan y Simonato (1995) y Filipovic y Trolle (2012). Esta representación es usada en esta investigación para mostrar el precio de dos activos financieros, como lo son el precio de un contrato colateralizado y otro activo no existente en el mercado que tiene en cuenta el riesgo de no-default, en función de dos variables estado que son la tasa de interés r(t) y el parámetro de no-default ξ(t).
Como se especificó en la ecuación (13), la tasa de interés instantánea sigue un proceso CIR de la forma:
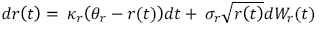 (B.1)
(B.1)Esta tasa de interés está presente en el precio de un contrato colateralizado que está expresado en las ecuaciones (2) y (14) y resumido como:
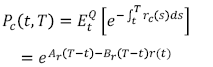 (B.2)
(B.2)donde las funciones Ar y Br tienen una única solución y son expresadas como:
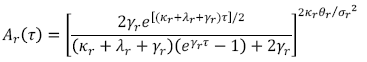 (B.3)
(B.3)
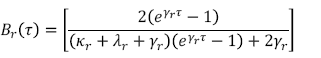 (B.4)
(B.4)A partir de la representación para el precio de un contrato no colateralizado, el precio de un bono cero cupón con riesgo de default está expresado por la ecuación (3) usando las intensidades de default obtenidas según la metodología expuesta en el Anexo A y presentadas en la figura 2.
Por otro lado, el activo no existente en el mercado que relaciona el riesgo de no-default viene expresado por la ecuación (15) expresada como:
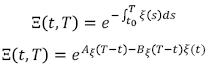 (B.5)
(B.5)En este caso, las funciones A ξ y B ξ son expresadas como:
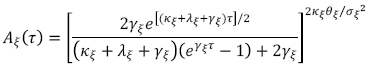 (B.6)
(B.6)
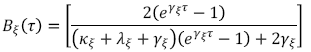 (B.7)
(B.7)Al igual que la tasa de interés instantánea, el parámetro de riesgo de no-default sigue un proceso CIR de la forma:
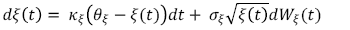 (B.8)
(B.8)Anexo C
Unscented Kalman Filter y estimación
El modelo está compuesto por variables estado que no son observadas en el mercado, para ello es necesario usar algún filtro que permita extraer de alguna variable observada dichas variables no observables o latentes. Adicionalmente, alguna de las ecuaciones de estimación no es lineal en las variables estado, como es el caso de la ecuación (8), por lo que este filtro debe permitir tener este tipo de interacciones. Para ello, Filipovic y Trolle (2012) usan el Unscented Kalman Filter (UKF), que es un filtro que permite extraer variables latentes a partir de variables observables y posibilita dichas relaciones no linealidades. Esta metodología se puede ampliar en Christoffersen et al. (2009) o en Wan y van der Merwe (2000).
Un Kalman Filter estándar tiene en la ecuación de pricing relaciones lineales entre las variables observadas y las de estado. En caso de no ser lineales, comúnmente se usa el Extended Kalman Filter (EKF) que incluye previamente una linealización de la ecuación de medición del modelo. Sin embargo, se ha venido usando mucho el UKF debido a que es menos restrictivo que los mencionados anteriormente. Este consiste en seleccionar puntos no aleatorios (sigma points) escogidos de tal manera que logren capturar la media y la covarianza de la variable aleatoria inicial; posteriormente, estos puntos son propagados mediante la transformación no lineal, de tal forma que logren capturar la media y la varianza de cualquier función no lineal. La selección y propagación de los sigma points es conocida como unscented transformation (UT) y es explicada por la figura C1 (Wan & van der Merwe, 2000).
El panel A la figura C1 muestra la forma en la que se estima la media y la covarianza de una variable aleatoria mediante simulación de Montecarlo. Esta no es una metodología apropiada debido a que el orden de convergencia de los Kalman Filter es mayor. El panel B muestra el EKF en caso de que fuera posible linealizar la ecuación de medición f(·). Esta metodología tampoco es la más acertada debido a que no es la más óptima y adicionalmente tiene restricciones con la relación entre las variables observables y las variables estado. Por último, el panel C muestra el funcionamiento de la UT, donde a partir de muy pocos sigma point se logra obtener la media y la varianza de las variables estado mediante la transformación de dichos puntos no aleatorios 24 . Cabe resaltar que la UT logra aproximaciones de segundo orden y hasta tercer orden en caso de que las variables estado tengan una distribución gaussiana 25 . Investigaciones como las de Christoffersen et al. y Wan y van der Merwe demuestran que el SR-UKF resulta ser la metodología que tiene el mejor performance en comparación con Montecarlo, KF lineales, EKF y los UKF estándar. Adicionalmente el SR-UKF garantiza que la matriz de covarianza de las variables estado sea semidefinida positiva.
El proceso de estimación se hace en conjunto con un SR-UKF y máxima verosimilitud. Este consiste en filtrar las variables estado a partir de cada ecuación de princing y de las variables observadas.
El proceso de estimación se hace en dos etapas:
1. En la primera etapa se filtra la tasa de interés instantánea r(t) (variable estado) a partir de las cotizaciones de los OIS siguiendo las ecuaciones (8) y (B.2). La representación estado espacio de esta primera etapa es de la forma:
- Ecuación de medición (measurement equation)
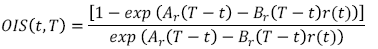 [C.1]
[C.1]donde Ar() y Br() están representadas por las ecuaciones (B.3) y (B.4).
- Ecuación de estado (state equation)
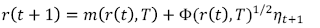 [C.2]
[C.2]con η t+1 un vector de variables aleatorias con media cero y varianza unitaria, m(r(t),T) = E[r(t + T)|r(t) y ϕ(r(t),T) = Var(r(t + T)|r(t)). Estas ecuaciones se cumplen para todos los T plazos disponibles en el mercado. A partir de la solución obtenida de PC (t,T), y la estimación de exp(–Γ(T)), según el Anexo A, se pueden encontrar los valores de B(t,T) siguiendo la ecuación (3). Posteriormente, con PC (t,T) y PC (t,T) se puede encontrar la estructura a plazos del riesgo de default descrita en la ecuación (17).
2. La segunda etapa consiste en filtrar y estimar los parámetros y la variable estado relacionada con el riesgo de no-default ξ(t). A partir de la estructura a plazos del riesgo de default y la del riesgo interbancario, se puede inferir el riesgo de no-default para cada plazo. Teniendo en cuenta las ecuaciones (9) y (17), se encuentra que el riesgo de no-default corresponde a:
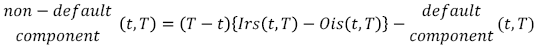 [C.3]
[C.3]Despejando Ξ(t, T)de la ecuación (5) se tiene que el factor de no-default está expresado como:
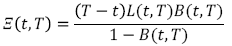 [C.4]
[C.4]Este factor se convierte en una variable observada en la segunda estimación y filtración de ξ(t). En este caso, la representación estado espacio de esta etapa se representa como:
- Ecuación de medición (measurement equation)
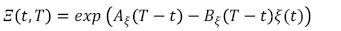 [C.5]
[C.5]- Ecuación de estado (state equation)
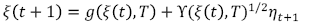 [C.6]
[C.6]con ηt + 1 un vector de variables aleatorias con media cero y varianza unitaria, y g(ξ(t), T) = E[ξ(t+T)|ξ(t)] y ϒ(ξ(t), T) = Var (ξ(t + T)|ξ(t)).
Anexo D
Índices de CDS usados en el modelo
Debido a la dificultad de contar un índice de los CDS que logre agrupar los bancos pertenecientes al panel de la Libor en dólares, se construyó un índice agrupando las cotizaciones de los spreads de los CDS individuales de cada índice. El índice de los CDS construido en esta investigación corresponde al promedio simple de los CDS de los bancos pertenecientes al panel de la Libor. Estos bancos fueron:
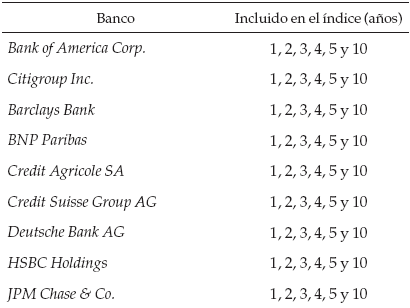
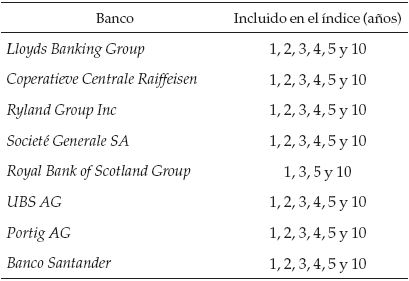
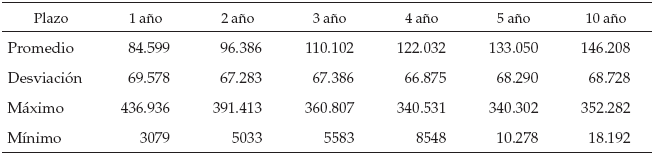
Los índices tienen las siguientes estadísticas y su comportamiento está descrito en la figura D1.
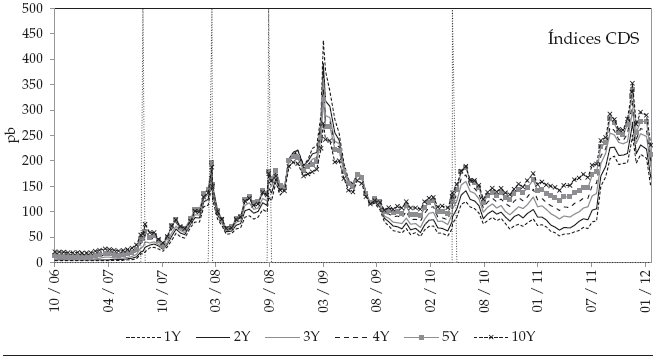
La estructura a plazos de las intensidades de default estimadas según el Anexo A se presenta en la figura D2.
Anexo E
Valores estimados para la prima de cobertura
Para aproximarse al valor de de la ecuación (1), que no es observable en el mercado y no existen plazos tan cortos en la estructura a plazos de los CDS, se tomaron distintos spreads que lograran medir la diferencia entre una tasa overnight (que se aproxima a libre de riesgo) y una tasa con riesgo. Para ello, se crea el spread resultante entre los OIS a 1 semana y distintas tasas repos existentes en el mercado. Estas tasas repos fueron: MBS GCF repo rate, Treasury GCF repo rate y Agency GCF repo rate. Estas tasas fueron extraídas de DTCC. El valor de fue escogido a partir de los promedios de cada uno de los spreads encontrados y presentados en la figura E1.
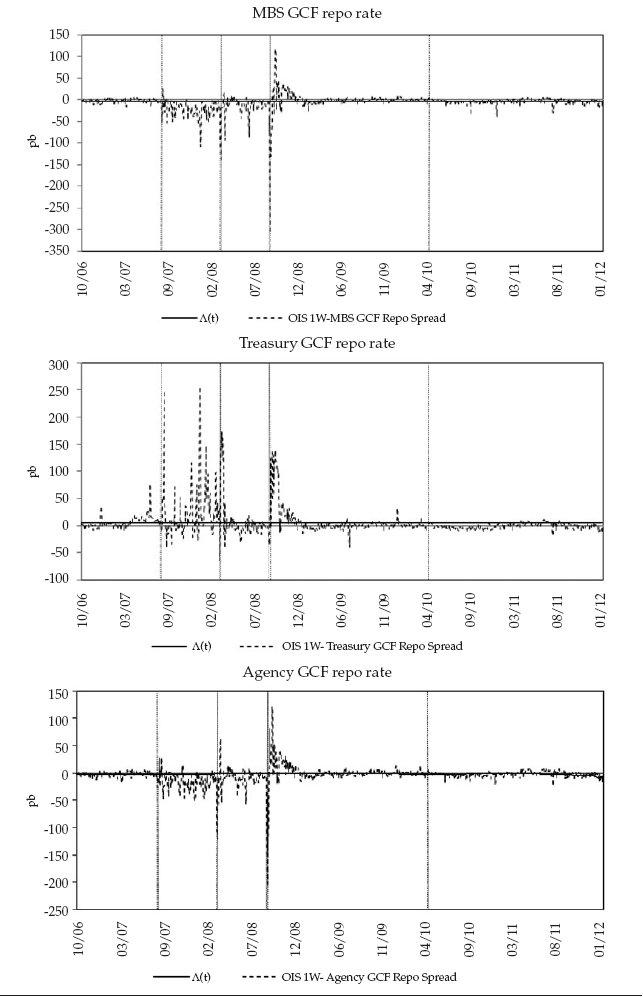
A partir de estos resultados, se escogió usar igual a 5,93 pb, cercano al valor escogido por Filipovic y Trolle (2012) que lo situaron en 5 pb.
Anexo F
Comparación con respecto al documento base
Como se mencionó anteriormente, esta investigación usó como referente la investigación llevada a cabo por Filipovic y Trolle (2012). Los autores miden el riesgo interbancario a partir de los mismos spreads usados en la presente investigación y utilizan una ventana de tiempo de estudio relativamente parecida. A pesar de que las técnicas de estimación usadas en ambas investigaciones es la misma, las investigaciones difieren en algunos detalles importantes de resaltar. Primero, la tasa de interés sigue procesos de difusión distintos: los autores lo describen bajo un proceso Vasicek, mientras que en la presente investigación es usado un proceso CIR. El parámetro de no-default ξ(t) sigue el mismo proceso (CIR).
Una de las diferencias más notorias es el proceso de filtración de las variables estado y la estimación de los coeficientes asociados con sus procesos de difusión. Filipovic y Trolle seleccionan las variables estado mediante un filtro de Kalman lineal multivariado y la estimación se hace en una sola etapa con tres variables estado y multifactoriales (incluyen una variable de deterioro crediticio y factores adicionales como valores de largo plazo de cada una de las variables estado). Por otro lado, esta investigación filtra las variables estado mediante el mismo filtro de Kalman no lineal pero univariado y en dos etapas (primero la filtración de la tasa de interés y posteriormente la variable de no-default ξ(t)).
Los resultados, en cuanto a los coeficientes encontrados, se muestran en la tabla F1. En este caso, los únicos parámetros comparables resultan ser los correspondientes a los del proceso de difusión de la tasa de interés, debido a la diferencia en el uso de un filtro multivariado y univariado y las etapas de filtración y estimación. La tasa de interés de largo plazo se encuentra cercana al 6,5 %, valor cercano a los estimados por Filipovic y Trolle. La tasa de interés instantánea converge más lento y adicionalmente es más volátil que lo encontrado por Filipovic y Trolle. El valor de ψ, entendido como el precio del riesgo en el mercado, es negativo para ambas investigaciones.
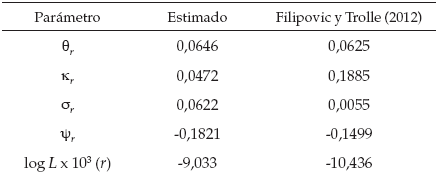
A continuación, se presentan algunas similitudes encontradas en ambas investigaciones en cuanto al comportamiento de las variables estado y los componentes del riesgo de interbancario. A pesar de las diferencias mencionadas anteriormente, no se encontraron disparidades considerables que puedan afectar los resultados y las conclusiones de ambas investigaciones.
Notas
*
Una versión previa de este trabajo fue presentada como Trabajo
de Grado de la Maestría en Finanzas Cuantitativas de la Facultad de Economía de
la Universidad del Rosario.
1
La crisis financiera de 2008 se originó en el mercado hipotecario de Estados Unidos, lo que afectó indirectamente los balances del sistema financiero internacional. Con los efectos de contagio y riesgo sistémico, rápidamente llegó a afectar las condiciones crediticias y la liquidez de importantes entidades como Washington Mutual, Merrill Lynch, JP Morgan, Bank of America, AIG y los sectores bursátiles e inmobiliarios del mundo.
2
Un contrato OIS (Overnight Indexed Swap) es aquel que intercambia una estructura de pagos en tasa fija por otra estructura a tasas variables indexadas compuestamente a una tasa overnight como los Tbills
3
Un contrato IRS (Interes Rate Swap) es aquel contrato celebrado entre dos partes que intercambian una estructura de pagos en tasa fija por otra estructura en tasa variable indexada a la Libor.
4
El Libor panel es actualizado cuando algún banco presenta un deterioro crediticio importante. Por lo general, estos cambios presentan cierta rigidez y un banco sale del panel algunos meses después del deterioro. Este hecho estilizado resulta dándole mayor riesgo crediticio a un panel rígido (Libor panel) que a otro actualizado de manera inmediata como lo es el mercado interbancario internacional.
5
Una tasa de interés instantánea es aquella en la que se acordarían prestamos en t conun vencimiento en T pero con T→t, de la forma:
r(t) = lim r (r, T)
T→t
6
Filipovic y Trolle (2012) asumen un modelo similar al de esta investigación y concluyen que distintos valores del parámetro no tiene importantes cambios, pero sí es necesario diferenciar entre estas dos tasas.
7
La intensidad de default es entendida como la probabilidad de que una entidad no pueda cumplir con los pagos de la deuda en un infinitesimal periodo.
8
Se asumió así, siguiendo lo propuesto por Brigo y Alfonsi (2006) quienes muestran que los cambios, incluyendo distintos niveles de correlación entre la tasa de interés y la intensidad de default, son casi nulos o poco significativos.
9
En 2008 se hizo público un estudio que sugería que la Libor habría sido alterada por grandes bancos, principalmente, en Norteamérica e Inglaterra. Estos bancos habrían reportado tasas Libor menores para alterar los costos de fondeo y aparentar ser bancos más sanos durante el inicio de la crisis.
10
La relación entre la función Ξ(t, T) y la variable de no-default está descrita en la ecuación (15).
11
Para ampliar sobre la especificación de este instrumento ver el Anexo A y
Brigo & Mercurio (2006).
12
Un modelo affine usa representaciones affines para poder expresar ecuaciones complejas y sin solución analítica, de una manera manejable y fácil de resolver. Esta representación consiste, por lo general, en la exponencial de una transformación lineal que relaciona la variable observada con la variable estado. De la forma: e-ʃxdx
= eα-βx
13
Este parámetro es conocido como el precio del riesgo en el mercado y es usado para que dWQ
(t) – ψ(t)dt sea un movimiento browniano estándar bajo la medida P mediante la transformación de Radom-Nikodym.
14
Para más detalle de estas representaciones, ver el anexo B, Filipovic y Trolle y Duffie, Filipovic y Schachemayer (2003).
15
Este filtro puede ser consultado en el Anexo C, Wan & van der Merwe (2000) y Christoffersen et al. (2009)
16
Existen algunos índices que agrupan los CDS de acuerdo con factores como sector económico, industria, ubicación, mercado, entre otros. Los índices más comunes son proveídos por la empresa de información financiera Markit. El índice Markit CDX Banks no está disponible para todo el periodo de estudio de esta investigación y, adicionalmente, está restringido para el público.
17
Existen trabajos como los de Liu, Longstaff y Mandell (2006), Schwartz (2010), Michaud y Upper (2008) entre otros, que analizan el riesgo interbancario y sus componentes, pero a partir de un análisis econométrico de estimación de ecuaciones de sensibilidad (Betas). En estos análisis, por lo general, hacen una regresión entre el riesgo interbancario y sus componentes como variable dependiente y los distintos factores que pueden afectar este riesgo como variables independientes. Estas investigaciones no estiman parámetros comparables con los estimados en esta tesis.
18
La correlación entre la tasa de la Fed y la tasa de interés instantánea es de 0,98. Las diferencias más grandes de estas dos tasas se encuentran durante los periodos de la crisis, tiempo en el que se alcanzó un spread entre 0,81 y -1,52 pb registrados en enero y junio de 2008.
19
Para ver la estructura a plazos de las intensidades de default ver la figura D2 del anexo D. Allí se presentan los CDS de la serie en frecuencia semanal.
20
Los puntos máximos de las intensidades de default de los CDS de más corto plazo coinciden el 9 de marzo de 2008, días previos a la venta de Bear Stearns el 16 de marzo de 2008 a J.P. Morgan Chase. Este fue el primer gran banco que no pudo evitar el colapso y fue vendido en US$10 la acción antes de haber alcanzado un máximo histórico de US$170 a principios de 2007.
21
Para marzo de 2009 Bear Stearns, Lehman Brothers, Washington Mutual, entre otras instituciones financieras habían salido del mercado por no poder cumplir con las obligaciones de la deuda.
22
Dado que este spread fue construido a partir de dos tasas que tienen efectos de default (más en el caso de la Libor que de los Tbills), es necesario ‘limpiar’ este spread de los efectos del riesgo de default que pudiera tener.
23
Esta segunda regresión se hace en diferencias debido a la existencia de raíz unitaria en las variables.
24
En el proceso de estimación, se calcula un conjunto de sigma points para cada observación, por lo que lo haría computacionalmente costoso. Sin embargo, es posible calcular una vez la matriz de varianzas y a medida que se tiene más información, actualizar recursivamente dicha matriz mediante una descomposición de Cholesky. La inclusión de esta actualización reduce el costo computacional y resulta ser más estable la estimación. A este filtro se le conoce como el Square Root Unscented Kalman Filter(SR-UKF).
25
Esta metodología resulta ser práctica para encontrar las L variables estado por el hecho que necesita únicamente 2L + 1 sigma points en la transformación UT.
Información adicional
Para citar este artículo: Cangrejo, G. A. (2016). La estructura
a plazos del riesgo interbancario. Revista de Economía del Rosario, 19(2),
129-174. Doi: dx.doi.org/10.12804/revistas.urosario.edu.co/economia/a.5617



